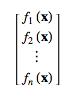a 와 b 가 서로소이고, 둘다 c 를 나누면, ab 도 c 를 나눈다.
증명) c = a k = b t , a x + b y = 1 ∴ c = a k ( a x + b y ) = a k ( a x ) + ab ( ky ) = b t ( a x ) + a b ( ky ) = ab ( tx + ky )
다음은 Euclid's lemma. 로 알려져 있다.
a | bc 이고, a 와 b 가 서로소 이면, a | c
증명) bc = ak , ax + by = 1 ∴ acx + bcy = c ∴ acx + aky = c ∴ a ( cx + ky ) = c
공약수를 d , 공배수를 m , 최대공약수를 g, 최소공배수를 ℓ 이라 하면, 다음이 성립한다.
증명) 1부에서 이미, 공약수가 공배수를 나눈다는 것을 보임으로써, 최대공약수가 최소공배수를 당연히 나눔을 보였었다.
또한, 1부에서, d | g 를 보였으므로, ℓ | m 을 보이는 것만 남았다.
a 와 b 의 공배수와 최소공배수를 m 과 ℓ 로 놓고, m 을 ℓ 로 나누는 디비전 알고리듬을 생각하자.
m = ℓ q + r ( 0 ≤ r < ℓ )
그러면, a와 b 가 m 과 ℓ 을 나누므로, 따라서, r 도 나누어야 한다. 즉, r 은 a 와 b 의 공배수가 된다.
그런데 범위가 ℓ 보다 작기 때문에, ℓ 이 최소공배수 라는 것으로 부터, r 은 0 이 된다. 이것으로 증명이 완료된다.
증명) a = g k , b = g k ' 이라고 놓으면, ab / g = ak' = bk 이므로, 따라서 a 와 b 의 공배수이다.
임의의 (양의) 공배수를 m 이라고 놓으면, m / ( ab /g ) = mg / ab = m ( ax + by ) / ab = (m/b) x + ( m/a ) y 가 된다.
그런데, m 이 a 와 b 의 공배수 이므로 (m/b) x + ( m/a ) y 는 정수이다.
따라서, m / (ab/g) 도 정수이다. 즉, ab/g 는 m 을 나누고, 따라서, ab/g ≤ m 이다.
공배수 ab/g 는 임의의 공배수 m 보다 작거나 같으므로, 최소공배수이다. 그러므로, ab / g = ℓ 이 된다.
곧바로, 다음의 코롤레리가 얻어진다.
a 와 b 가 서로소 이면, ℓ = ab 이다.
다음의 것도 자주 사용된다.
a = g s , b = g t 이면, s 와 t 는 서로소 이다.
사실 이건 1부에서 이미 증명한것이다. a x + b y = g 에서 양변을 g 로 나누면 (a/g) x + (b/g ) y = 1 로 (a/g) 와 (b/g) 가 서로소.
여기서 부터는, gcd ( , ) , lcm( , ) 보다 더 간단한 표현으로 ( , ) , [ , ] 을 쓰기로 한다.
그러면, "a와 b는 서로소 이다" 는 간단히 (a,b) = 1 로 쓰면 된다.
증명) (a,b) | a | ac , (a,b) | b | bd 그러므로, (a,b) 은 ac 와 bd 의 공약수이다. 그러므로 (ac,bd) 를 나눈다.
증명) (ka,kb) = positive min{ kax + kby } = |k| positive min{ ax + by } 증명끝.
다음은 정리는 매우 중요하다.
(ab,cd) = 1 ⇔ (a,c) = (a,d) = (b,c) = (b,d) = 1
증명) 왼쪽에서 오른쪽으로 의 증명은 abx + cdy = 1 부터 자명하므로, 오른쪽에서 왼쪽으로 증명만 남는다.
이것은 (a,c) = (b,c) = 1 ⇒ (ab,c) = 1 임을 증명하면 충분하다.
왜냐면, c 대신 cd 로 치환하면, 연쇄적으로 적용돼서 원하는 증명이 되기 때문이다.
따라서, (a,c) = (b,c) = 1 ⇒ (ab,c) = 1 만 증명하면...
ax+cy = 1 , bu + cv = 1 이고, 두식을 곱하면, ab (xu ) + c ( buy + axv + cyv ) = 1 이므로, 증명이 끝난다.
위의 정리로 부터 다음의 정리는 간단히 증명된다.
(a,b)=1, c|a 이면 , (c,b)=1
증명) ( a,b ) = 1 이고 c | a ⇒ ( ck , b ) = 1 ⇒ (c,b) = (k,b) = 1 증명끝.
(a,b)=1 이면 (ac,b) = (c,b)
증명) 우선 (c,b) | (ac,b) 는 당연하므로, (ac,b) | (c,b) 임을 보이면 충분하다.
ax + by = 1 ⇒ acx + bcy = c , 여기서 (ac,b) 가 ac 와 b 를 나누므로 , 우변의 c 도 나눈다. 증명끝.
(a,b) = 1 이면 ( a , b+ka ) =1
증명) ax + by = 1 ⇒ ax - kay + kay + by = 1 ⇒ a ( x - ky ) + (b + ka ) y = 1
(a,b) = 1 이고 d | ac ∧ d | bc 이면 d | c
증명) ac = ds , bc = dt , ax + by = 1 ⇒ acx + bcy = c ⇒ dsx + dty = c ⇒ d ( sx + ty ) = c
(a,b) = 1 이면 ( an , bn ) = 1
증명) ( a
2 , b ) = 1 을 보이면 충분, 연쇄적으로 적용하면 되니까.
ax + by = 1 ⇒ ( ax + by ) 2 = 1 ⇒ a2 ( v 2 ) + b ( 2 axy + by2 ) = 1
(a+b,a-b) | (a+b) ± (a-b) ∴ (a+b,a-b) | 2a , (a+b,a-b) | 2b ∴ (a+b,a-b) | (2a,2b) ∴ (a+b,a-b) | 2 (a,b) ∴ (a+b,a-b) | 2
∴ (a+b,a-b) = 1 또는 2