Conditional Statements
컨디셔널은 보통 논리기호로 → 로 쓰고 , 우리말의 "~이면 " 정도로 표현된다.
( " p → q " is read " if p , then q " and so on )
우리는 아래에서 implication(함의) 와 conditional 과 구분하여 정의했지만, 교재에 따라 구분하지 않고, 컨디셔널을 implication 으로 부르기도 한다.
컨디셔널의 연산자 우선순위는 논리곱(conjunction) ∧ 이나, 논리합(disjunctin) ∨ 보다 늦는걸로 약속한다.
컨디셔널에 대한 트루뜨 테이블은 다음과 같이 정의한다.
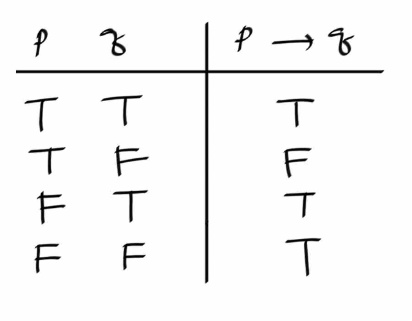
이때 p를 hypothesis 가정 (antecedent 전건, premise 전제 등) 이라 하고, q 를 conclusion 결론 ( consequent 후건, consequence 결과 등) 이라고 한다.
보다시피, 오직 결론이 거짓이고 가정이 참일때에만 주어진 명제를 거짓으로 평가한다.
즉, 컨디셔널이 참으로 평가된다고 해서, 가정과 결론사이의 본질적 인과관계를 보장하지는 않는다.
첫줄부터 보자. 가정이 참이고 결론이 참이면, 컨디셔널은 참이다. 그러나 그렇다고 해서 가정과 결론사이에 본질적인 인과관계가 있다고 할 수 있는가? 없다. 물론, 우리는 충분히 그것이 무의미한 명제인지 아닌지 골라낼 자신이 있다고 생각한다. 물론 많은경우 그렇긴 하지만, 때때로 그것은 착각이고, 그로인해 자주 확대해석의 오류를 범하곤 한다.
첫번째 줄에 대한 예를 들어보자. " 1+1=2 이면 3은 홀수이다. " 이 명제는 참이다. 그러나 우리는 1+1=2 이기 때문에 3이 홀수다 라고 말하는데에는 초큼 주저하게 된다. 물론, 1+1=2 였기 때문에 3이 홀수인지도 모른다 ;;; 그게 얼마나 convincing 한지는 모르겠지만...
두번째 줄을 보자. " 1+1=2 이면 3은 짝수이다. " 는 거짓이다. 뭐랄까. 이런 뉘앙스는 어떨까? " 1+1 =2 로 잘 맞음에도 불구하고 3이 짝수라니 그것참 이상하군 ! "
세번째 경우, " 1+1=3 이면 4는 짝수다." 결론만 맞으면 참이군 ! 그렇다 가정이 틀려도 참이다.
더 재밌는건 네번째다. 가정이 틀리면 아예 결론에 상관도 없이 다 참이 된다. " 1+1=3 이면 3은 짝수다." 이게 참이라고? 이건뭐 걍 다 파토내자는 분위기? 세번째 까지는 납득 혹은 납득했다고 착각하는데 크게 어려움이 없을지도 모르겠다. 그러나 네번째는 어떠한가?
이것을 납득하기 위해 다음의 말이 구라인지 살펴보자. "니가 김태희면 나는 장동건이다."
내가 박지선이나 신봉선한테 저렇게 말했다고 해도, 우리는 이걸 구라라고 하지 않겠다는 거다. 왜냐 니가 김태희가 아니니까. 대략 그런 느낌적인 느낌?
저렇게 말했는데 내가 구라쟁이가 되는 경우는 오직 "상대방이 진짜 김태희 맞는데 나는 장동건이 아닌" 그런 경우가 되겠다. 이때는 대략 낭패.
컨디셔널 스테이트먼트에 대해, 우리가 말할 수 있는 것은 다음과 같다.
1. 결론이 참이면 무조건 참이다.
2. 가정이 거짓이면 무조건 참이다.
3. 그럼 언제 거짓? 가정은 참인데 결론이 거짓일때에만 거짓이다. 나머지는 모두 참.
자 우리는 이러한 논리의 바탕위에서 수학을 펼치고 있는것이다. 물론, 이러한 논리의 기초위에서 수학의 체계를 세우는데 모두다 찬성했던것은 아니다. 반대한 사람도 많았고, 그들도 그들 나름대로의 논리학을 정립하기도 했다고....
처음에도 말했지만, 우리는 컨디셔널이 참이더라도, 그것이 무의미할 수 있으며, 그것을 가려낼 수 있다고 생각한다.
tautology(항진명제) 와 contradiction(모순)
항상 참인 명제를 tautology(터탈러지) 라고 하고, 항상 거짓인 명제를 contradiction(컨트러딕션)이라고 한다.
가령, p ∨ ¬p 는 터탈러지이고, p ∧ ¬p 는 컨트라딕션이다.

즉, 수학에서는, 임의의 명제에 대해, 그것은 참 또는 거짓 둘중에 하나이며, 참이면서 거짓일수는 없다.
tautology 를 간단히 첫글자 t 로 나타내거나, 항상 참값으로 평가되므로 아예 T로 쓰기도 한다.
마찬가지로, contradiction 은 c 나 F 로 쓰곤 한다.
참고로 tautology 도 contradiction 도 아닌경우를 간혹 contingency 라고 하기도 한다.
Implication
조건문 p → q 가 tautology 일때, p ⇒ q 로 나타내기로 하고, implication (함의) 이라고 한다.
( 텍스트북에 따라, p → q 을 implication 으로 부르기도 한다.)
p ⇒ q 는 " p implies q " 또는 " p entails q " 따위로 읽는다.
다음은 implication 의 몇가지 예이다.
p ⇒ p
p ⇒ p ∨ q
p ∧ q ⇒ p
( p ∨ q ) ∧ ㄱp ⇒ q
F ⇒ T
위의 예 중에서 4번째 것을 트루뜨 테이블로 증명해보자.
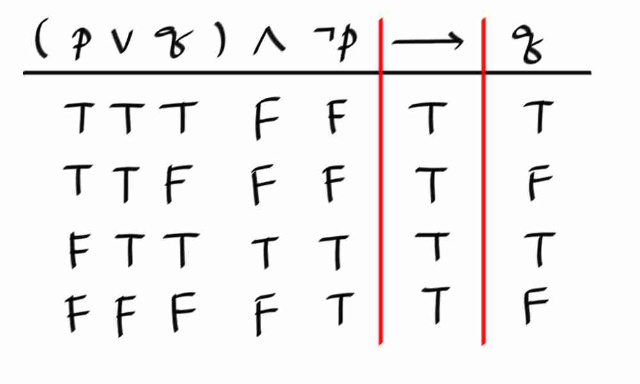
위의 심플러파이드 트루뜨 테이블을 보는 법은 논리연산자의 우선순위를 따르며, 첫번째 스텝은 독립 논리변수들로 부터 시작한다.
위의 표에서 보듯이, 최종적으로 → 의 평가가 모두 T 가 되었으므로, 위의 명제는 tautology 이다. 즉, ( p ∨ q ) ∧ ㄱp ⇒ q 가 된다.