라다 RADA - Sexy Baby Story
Music2008. 9. 25. 23:27 |매튜 & 워커 - 수리물리 데자 부 파일
Misc.2008. 9. 9. 10:52 |이것이 C525A 의 단아한 자태.....라고 하기엔 조금 덩치.

퀄리티야 뭐 말할것도 없지만, 역시 최대장점이라면 랜카드가 장착되어있다는것. 공유기에 꼽아서 쓰면 동시에 여러컴퓨터에서 사용 가능하다. usb로 한대에 연결한다음 네트워크 공유해서 쓰는것과는 차원이 다르다. 지금 내가 그렇게 쓰고있지만 여간 불편한게 아니다.
사실 싸이즈 큰건 별로 상관없었다. 뭐 크면 용지함도 엄청 클테고 뭐 그닥 나쁠것도 없었다. 그냥 핑계고, 가격이 좀 빡세서 못샀다는게 솔직한 심정. 뭐 잘 찾아보면 40만원대에 구할수 있다고 하는데 나는 뒤지고 뒤져도 자꾸 60만원대만 뜨는거다.
암튼, 결국 차선책으로 c1110 구입했다. 이것이 C1110 의 컴팩트한 디자인.

뭐 c525a 보단 나름 한참 신모델이니 많은 개선이 있었다고 하는데 디자인은 그래도 c525a 가 더 이쁜것 같다. 뭐 새로운 소재를 채택해서 부피를 많이 줄였단다. ( 뭐 나랑 큰 상관은 없다. )
환경 어쩌고가 어쩌고해서 칼븐 다이악사이드 배출량을 50 퍼센트 감소시켰다는데 역시 나랑 큰 상관은 없다. 뭐 환경보호에는 좋은가보더라. 아무튼 다 나한테는 그닥 상관없고, 젤 중요한건 랜카드가 장착되어있으면서 가격이 35만원 정도 한다는 거다.
그거면 됐다.
사실 c525a 가 디자인이 더 맘에 들긴 하는데 크기가 너무 큰것도 그렇고 무거운것도 그렇고 ...
그래도 c525a는 나온지 오래됐으니까 새로나온 c1110 이 좀 개선되지 않았을까
그리고 CO2 배출량을 50% 감소시켜서 환경무슨 상도 받았다고 하니까

독일식 영어억양이 굉장히 독특하신 롤랜드 브라이텐펠트 ( Roland Breitenfeld ) 선생님
근데 발음 들으니 롤랜드가 아니라 홀랜드 처럼 들렸...

전자음악실 내부.




저거 다 배우게 되는걸까.... 두근두근
교수님이 만든 26분짜리 음악을 감상했는데, ㅎㄷㄷㄷ 26 세기 정도의 음악이랄까....
속으론 " 왓더... 이게 대체 뭐야 ....? " 하지만 공식적으론 " '난해한' 음악이네요." 그리고 교수님 앞에선 " 짝짝짝!!! " 교수님은 " 땡스~ 감사합니다 ^^ "
나는야 가식 덩어리 ;;;
[중학수학] 삼차함수 그래프 : 변곡점에 대해 대칭
Math2008. 8. 29. 01:04 |
이따위로 그린다거나.... 하면 안되는거다. 별 신경안쓰고 저따위로 많이 그렸었는데... 아무튼, 변곡점에 대해서 대칭이라는 사실.
3차 함수 일반식을 f(x) = a x^3 + b x^2 + c x + d 라고 놓으면,
변곡점에 대해 대칭이라는 게 그닥 당연스러워 보이지는 않는다.
증명을 위해, 일단 변곡점의 좌표를 ( p , f(p) ) 라고 놓자. 그러면 변곡점에선 두번미분하면 0 이니까...
f''(x) = 6 a x + 2 b 는 x = p 에서 0 이어야 할테고, 따라서...
3 a p + b = 0 이다.
이제 3차함수의 그래프 y = a x^3 + b x^2 + c x + d 를 변곡점이 원점으로 오도록 , x축 방향으로 -p 만큼, y 축 방향으로 - f(p) 만큼 평행이동 해보자. 그러면...
y + f(p) = a ( x + p )^3 + b ( x + p )^2 + c ( x + p ) + d
전개하면...
y = a x^3 + ( 3 a p + b ) x^2 + ( 3 a p^2 + 2 b p + c ) x + a p^3 + b p^2 + c p + d - f(p)
그런데, f(p) = a p^3 + b p^2 + c p + d 이므로...
y = a x^3 + ( 3 a p + b ) x^2 + ( 3 a p^2 + 2 b p + c ) x 가 되고,
게다가, 3 a p + b = 0 였으므로,
y = a x^3 + ( 3 a p^2 + 2 b p + c ) x 이 된다. 보다시피 원점대칭이 된다.
따라서 본래의 3차함수 그래프는 변곡점에 대해 대칭이다.
[C언어] 자기참조 구조체에 의한 연결 리스트 (Linked List) 구현
COM2008. 8. 17. 08:09 |In computer science, a linked list is a data structure that consists of a sequence of data records such that in each record there is a field that contains a reference (i.e., a link) to the next record in the sequence.
Each record of a linked list is often called an element or node.
The field of each node that contains the address of the next node is usually called the next link or next pointer. The remaining fields are known as the data, information, value, or payload fields.
-----------------------------------------------------------------------------------------------------
자료구조 "Linked List" 를 C로 구현하는 방법에 대해 알아보자.
링크트 리스트를 구현하기 위해서는,
데이터들이 자신과 같은 타입의 데이터를 포인팅하는 정보를 포함해야한다.
즉, 데이터 타입 내부에 자신과 같은 타입에 대한 포인터를 가지고 잇어야 한다는 말이 된다.
struct list { int data; struct list *p; };
이제 이러한 형의 데이타를 선언해주면 이러한 타입의 변수들을 만들수 있고, 그것들을 서로 연결시키면 된다.
sturct list a,b,c;
a를 b로 연결시키고, b를 c로 연결시키고, c는 매듭을 지어보자. 마지막노드로 매듭을 지을때는 포인터를 널포인터로 만들면 된다.
a.p = &b;
b.p = &c;
c.p = NULL;
연결 리스트의 특징은, 데이터들이 줄줄이 사탕으로 엮여있기 때문에, 줄줄이 사탕중 어느 하나를 잡으면, 그 것으로 부터 이어진 데이터에 접근이 가능하다는 것이다.
즉, 위의 예에서, 노드 b 에 접근을 했다면, 거기서 c로 접근을 할 수 있다.
b에서 c의 데이터에 접근하는 방법은 아래와 같다.
b.p -> data
만약 a에서 c의 데이터에 접근하고 싶다면 다음과 같이 된다.
a.p -> p -> data
이렇게 하면, a에서 b의 포인터로 접근하고 b의 포인터가 가리키는 노드로 간후에 거기서 데이타에 접근한다.
이러한 연결 리스트를 이용하여, 순차적으로 접근 가능한 데이터를 다룰 수 있다.
그리고, 연결리스트를 통해서도 스택이나 큐를 구현할 수 있는데, 이에 대해서는 나중에 살펴본다.
각종 리스트 구조 (linear linked list, circular linked list, multiple-linked list 등등) 와, 각종 리스트 연산에 관해서는 나중에 따로 다루기로 한다.

수천번 수만번을 봐도 질리지가 않는다.
단 한번도 똑같았던 적이 없다.
어릴적에 경사진 터에 누워 밥먹는것도 잊은채 하루종일 구름만 본적도 있다.
하지만 여전히 구름은 나의 마음을 끈다.
Damien Rice - The Blower's Daughter
Misc.2008. 7. 16. 11:18 |MIT-OCW. Linear Alegbra. Lec. 1. Spring 2005.
Math2008. 7. 10. 00:40 |MIT-OCW Linear Alegbra. Lec. 1. Spring 2005.
http://www.youtube.com/watch?v=gVMRuLH6FdQ
[윈도우팁] IE 빈페이지 , 새창으로 바로가기
COM2008. 7. 8. 22:50 |새창으로 바로가기.

[C언어] atoi() , atol() , atof() , strtol() , strtoul() , strtod()
COM2008. 7. 8. 19:41 |Converting Strings to Numbers.
ato...() 와 strto...() 부류의 함수들은 문자열을 값으로 변화하기 위해 사용된다. 헤더는 stdlib.h 이다.
a 는 alpha(또는 ascii) 를 나타내고, str 은 string 을 나타낸다. strto...() 부류는 ato...() 부류에 비해 더 많은 제어와 오류검색을 제공한다.
ato...() 부류
atoi()
오래전부터 정말 많이 쓰이던 함수로, 일명 아토이 함수라고도 불린다. 보통은 a to i 라고 읽는다. i 는 integer를 나타낸다. 문자열을 정수로 변환한다.
int atoi(const char* );
숫자가 아닌 문자들은 delimiter로 작용한다. 따라서 초반에 숫자 아닌 문자가 오면 변환이 안된다. 변환이 안될경우 0 을 리턴한다. 단, 문자열 초반의 whitespace 에 대해서는 무시한다.
예.
#include<stdio.h>
#include<stdlib.h>
int main(void) {
char str[30];
scanf("%s",str);
printf("%d\n",atoi(str));
return 0;
}
atol()
atoi() 와 같은데, 다만 변환이 long 형이다.
long atol(const char* );
atof()
이것은 floating-point 특히, double형으로 변환한다. period (.) 도 소숫점으로 인식한다.
double atof(const char* );
다음은 위의 예제 코드와 동일하되, %d 대신 %lf 를 , atoi 대신, atof 를 쓴것이다.
---------------------------------------------------------------------------------------------------------------------
strto...() 부류
strtol()
문자열을 long 형으로 변환하고 리턴한다.
long strtol(const char* , char** , int );
첫번째 인자는 변환할 대상 문자열이다.
두번째 인자는 변환이 멈춘 지점의 "포인터의 주소"를 넘겨줄 대상이다. 즉, char** 형 변수가 와야한다. 이것을 NULL 로 설정하면, 멈춘 지점부터 시작하는 문자열을 아무곳에도 저장하지 않는다.
세번째 인자는 기수법의 밑(base)이다. 2부터 36 까지의 값을 갖는다.
이값은 변환할 문자의 범위를 지정하는 것으로, 가령 2 라고 하면, 문자열을 2진법으로 받아들여서 변환한다. 따라서, 0 과 1 만 변환을 수행하고 나머지는 delimiter 가 된다. 또 밑이 10 을 넘는 경우에는... A (또는 a ) 는 10 , B (또는 b ) 는 11 , ... , Z (또는 z) 는 35 과 같은 식으로 변환한다. 이때, 밑에 따라서 받아들이는 값도 그 진법에 맞게 해석된다. 따라서 변환된 값을 10진법으로 출력할 경우, 입력한 스트림과 다른 값이 나오게 된다.
특히, base를 0 으로 설정하면, 입력한 스트림의 첫부분에 의해 베이스를 8, 16, 10 으로 유연하게 적용할 수 있다. 첫부분이 0x ( 또는 0X ) 이면, base를 16 으로 해석한다. 첫부분이 0x 는 아니면서 0 이면, base를 8 로 해석한다. 나머지 경우는 base 10 으로 해석한다.
오버플로우 발생시, LONG_VAL 이나 -LONG_VAL 을 리턴하고, ERANGE 가 errno 에 저장된다.
예.
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int main(void) {
int base; long converted; unsigned i; char str[30] , *stop;
printf("Input a string starting with a positive integer : "); scanf("%s",str);
printf("Input the base ( 2 ~ 36 ): "); scanf("%d",&base);
converted = strtol(str,&stop,base);
for(i=0;i<(strlen(str)-strlen(stop));i++)
printf("%c",str[i]);
printf(" (%d)\t->\t%li (10)\n",base,converted);
return 0;
}
실행화면.
참고로 오류처리 부분만 제외하면... atol(str) 는 strtol ( str , NULL , 10 ) 와 같고,
atoi(str) 는 (int) strtol ( str , NULL , 10 ) 와 같다.
strtoul()
이것은 strtol() 과 유사하지만, unsigned long 을 리턴한다. 오버플로가 발생되면, ULONG_VAL 이나 -ULONG_VAL 이 리턴된다.
unsigned long strtol(const char* , char** , int );
strtod()
이것은 문자열을 double 로 변환한다. 첫번째 인자와 두번째 인자의 의미는 strtol() 과 같다.
double strtod( const char* , char** );
오버플로우가 발생되면, HUGE_VAL 이나 -HUGE_VAL 이 리턴되고, 언더플로가 발생되면 0 이 리턴된다. 두경우 모두 ERANGE가 errno 에 저장된다.
[C언어] 데이터 packing 과 다중바이트(multi-byte) 문자
COM2008. 7. 5. 01:00 |char 형이 int 로 승격될때, 4바이트 중에 하위 1바이트에 들어가기 때문에, 비트연산자로 8비트씩 위로 밀어주면서 글자를 넣어주면 된다.
언패킹 할때도 마찬가지다. int에서 char형으로 캐스트되면 하위1바이트만 받아들인다.
따라서, 간단히 생각할때, 언패킹하는 함수를 만들자면, 패킹된 int 와, 몇번째 바이트를 꺼낼지를 나타내는 수를 하나 받아서, 원하는 바이트가 하위바이트로 오도록 하면된다.
---------------------------------------------------------------------------------------------
예. packing
int pack;
pack = 'm';
pack = ( pack << 8 ) | 'a' ;
pack = ( pack << 8 ) | 't' ;
pack = ( pack << 8 ) | 'h' ;
이제, pack 을 이진수로 찍어보면 다음과 같다.
01101101 01100001 01110100 01101000
이것은 m a t h 의 아스키코드들이다.
언패킹 하는 함수는 간단히 다음과 같이 만들수 있다.
char unpack(int p,int k)
{
return ( p>>((4-k)*8) );
}
마스크를 써도 되는데, 이때는 마스크를 8개의 연속하는 1 ( 즉, 1바이트 모두가 1 ) 과 나머지 3바이트의 0 으로 마스크를 만든다. 그리고 비트이동 연산자를 사용해서비트이동 연산자를 사용해서 꺼내고자 하는 바이트위로 8개의 1이 위치하도록 만들고, 비트 논리곱을 쓰면, 해당 바이트는 그대로 유지가 되고 나머지 바이트는 0으로 없어진다. 그리고 다시 해당바이트를 최하위 바이트로 이동시켜서 char 로 리턴시키면 된다.
어차피 값에의한 호출을 하기때문에 함수의 몸체안에서 쓸데없는 값을 다 0으로 없애도 원래의 퍀킹된 정보는 손실되지 않는다.
아래 그림은, int 변수 하나에 문자 네개 m, a, t, h 를 패킹한후에, 위의 언패킹 함수로 각각 꺼낸모습이다.
----------------------------------------------------------------------------------------------------
다중바이트 문자
위에서, 1바이트 char 형 문자4개를, 4바이트 int 형에 패킹하는 모습을 보았다.
ANSI C 에서는 다중바이트 문자로 이러한 패킹을 직접 제공한다.
가령, int a = 'math' ; 라고 하면, 'm' , 'a', 't', 'h' 가 패킹된다.
패킹방식은 시스템 의존적이다. 내 경우에는 'math' 에서 m 부터 하위바이트로 들어가서 상위로 밀어내며 이후 문자들을 패킹되는 것을 확인할 수 있었다. 즉, 위의 실행결과와 같았다. 가령, a = 'mat' 라고 하면, 하위 3개 바이트에 패킹되었다.
사이즈보다 큰 다중바이트 문자가 패킹시도되면 에러가 난다.
[역학] 시간미분과 좌표미분의 교환
Physics/Math./Mech./Gen. Relativity2008. 7. 4. 02:36 |

[역학] 위치의 일반화좌표 미분 = 속도의 일반화속도 미분
Physics/Math./Mech./Gen. Relativity2008. 7. 1. 23:30 |다음의 증명에서, qj 는 generalized coordinate 이고, qj 의 닷은 generalized velocity 이다.

[C언어] 문자열 처리 함수 strcpy() , strcat(), strcmp(), strlen()
COM2008. 7. 1. 11:52 |strcpy() string copy 문자열 복사
헤더파일: string.h 문자열 함수 헤더
프로토타입: char* strcpy( const char* , const char* );
두번째 인자인 문자열을 첫번째 인자인 문자열에 덮어쓰기로 카피한다.
리턴값: 첫번째 인자인 문자열
첫번째 인자에서 확보된 메모리가 두번재 인자의 크기보다 작지않아야 한다.
문자 배열(문자열상수)의 경우 초기화 선언을 제외하고는 직접 배정문으로 문자열을 집어넣을수가 없다.
즉,
char arr[100]; 으로 선언되어 있는 상태에서
arr = "Hello! Nice to meet you."; 는 에러이다.
두번째 줄이 에러가 되는 과정은 다음과 같다ㅏ.
1. 첫번째 줄의 배열 선언에서, 메모리 100바이트를 잡는다.
2. arr 은 그 메모리의 시작 주소이다. (상수로서 이후에 변경이 불가하다)
3. 두번째 줄에서 우선 문자열상수 "Hello! Nice to meet you." 를 어딘가에 저장한다.
4. 그 주소를 arr 에 대입하려고 한다. 즉 arr 를 그 주소로 포인팅 하려고 하나, arr이 상수이므로 변경이 불가하여 에러가 난다.
이럴때 다음과 같이 strcpy() 를 사용할 수 있다.
strcpy(arr,"Hello! Nice to meet you.");
strcpy()의 프로토타입에서 보듯이, 인자들은 const char* 이다. 즉, 포인터 자체를 변화시키지 않는다. 단지, 포인터가 가리키는 위치를 받고, 그 위치에서 한칸씩 이동하며 문자를 복사하는 행위를 하는 함수이다. 이 행위는 널문자를 만날때까지 계속된다.
---------------------------------------------------------------------------------------------------
strcat() string catenate ( string concatenate ) 문자열 덧붙이기
헤더파일: string.h
프로토타입: char* strcat( char* , const char* );
두번재 인자인 문자열을 첫번째 문자열에 덧붙인다.
리턴값: 첫번째 문자열
첫번째 문자열의 널문자 위치에 두번째 문자열의 첫글자가 덮어지며 이어붙여진다. 첫번째 인자는 두번째 문자열이 붙을 만큼의 충분한 공간이 확보되어있어야한다.
---------------------------------------------------------------------------------------------------
strcmp() string compare 문자열 비교
헤더파일: string.h
프로토타입: int strcmp(const char*, const char*);
첫번째 문자열과 두번재 문자열을 사전적 순서로 비교(렉시코그래피컬리) 하여, 첫번째가 크면 양수, 작으면 음수, 같으면 0 을 리턴한다.
---------------------------------------------------------------------------------------------------
strlen() string length 문자열 길이
헤더파일: string.h
프로토타입: size_t strlen(const char*)
NULL 문자를 뺀 문자의 개수를 리턴한다. size_t 형은 4바이트 int 시스템에서는 unsigned int 이고, 2바이트 int시스템에서는 unsigned long 이다.
[고등학교수학] 케일리 - 해밀턴에 대한 주절거림
Math/Algebra(Abstract & Linear)2008. 7. 1. 01:56 |어제 과외하다가, 케일리-해밀턴 정리를 설명하는데, 애초에 교육과정에서 빠진데다가, 주어진 것은 2x2 이차 행렬방정식 하나.... 확실히 문제풀때, 강력한 툴임에는 틀림이 없는바 적당한(?) 수준에서 설명을 했지만, 억눌렀던 이야기를 더듬어 본다.
어떤 일차변환에 대해서 대응되는 행렬이 있고, 그러한 변환에 대해 어떤 벡터는 변환해도 고작 스칼라배밖에 안되는 녀석들이 있는 경우가 있다. 0벡터는 항상 그렇게 되겠지만, 트리비얼하므로 논외로 하자. 아무튼, 그러한 벡터들은 그 행렬의 고유한 속성을 나타낼 것이다. 가령, 공간에서 회전시키는 행렬에 대해, 회전축성분의 벡터는 회전에 대해 불변일 것이다. 그리고 그 회전축 방향의 벡터는 그 회전행렬의 고유한 속성이라고 할 수 있다. 그래서, 우리는 그러한 0아닌 벡터들을 아이겐벡터(고유벡터)라고 하고, 스칼라값을 아이겐벨류 (고유값) 라고 한다. 그리고 그러한 고유값들을 그 행렬의 고유값들 이라고 한다. 이때, 모든 아이겐벡터로 생성되는 공간을 아이겐스페이스(고유공간)라고 한다.
행렬이 고유값을 갖을려면, 임의의 고유값을 λ 라고 했을때, ( A - λ I ) x = 0 이 논트리비얼 솔루션을 갖어야 한다는 말이되므로, 결국, det ( A - λ I ) = 0 이 되어야 한다. 여기서 det ( A - λ I ) 을 그 행렬의 characteristic polynomial (특성다항식) 이라고 하고, 그것을 0 으로 놓은 방정식을 특성방정식 이라고 한다.
참고로, 대칭행렬의 경우, 직교대각화에 대한 필요충분조건을 주며, 결국, main diagonal ( / 다이 애 그널 / 이라고 읽어야 한다. 강세는 '애' 에 있다. 다이어고날이 아니다. ) 들이 고유값이 된다. 행렬의 대각화와 군론의 컨주게이션의 유사성이 새삼 신기하다. similar transformation 을 하면, 고유치가 불변이고, 어떤 그룹의 노말서브그룹은 컨주게이션에 대해 불변이다. 당연한 얘기지만, 삼각행렬도 대각선성분들이 고유값들이다.
다시 케일리 해밀턴으로 돌아가기 위해, 특성방정식 det ( A - λ I ) = 0 을 살펴보자. 여기서 λ I 대신에, A 를 집어 넣으면 det 0 이 되어 방정식은 트리비얼하게 만족될 것이다.
고등학교때로 돌아가기 위해, 2x2 행렬을 고려하자. 흔히 놓는대로, 각 성분을 a , b , c , d 라고 놓고, 특성방정식을 구하면, ( a - λ ) ( d - λ ) - bc = 0 이 될 것이다.
전개하면, λ² - ( a + d ) λ + ( ad - bc ) = 0 이 된다. trace 와 detetminant 를 도입하여 좀더 간단히 써도 좋은데, 참고로 트레이스와 디터미넌트는 similar transformation 에 대한 인베리언스들이다.
아무튼, 여기에 양변에 I 를 곱하고 , λ I 대신 A를 넣고 싶은 생각이 든다. 그러면 식은 A² - ( a + d ) A + ( ad - bc ) I = 0 이 되고 고등학교때 배운 버전의 케일리-해밀턴 식이 튀어나온다. ( 이것은 단지 직관적인 "스토리"로써 , 케일리-해밀턴 정리의 증명은 아님은 밝혀둔다. : 댓글 지적후 추가됨 ) 케일리 해밀턴 정리가 특성방정식과 관련이 있다는 것으로 부터 그것이 단지 2차에 국한되는 내용이 아닐것이라는 생각이 들어야 할 것이다. 그러나 여기서는 2차에 국한시키기로 한다.
수1 정석에 보면, 케일리 해밀턴 정리의 역은 성립하지 않는다 는 말이 나온다.
그렇다면, 케일리 해밀턴의 역은 무엇인가? 그리고, 왜 성립하지 않으며, 만약 성립한다면 언제 성립하고, 성립하지 않는다면 언제 성립하지 않는가? 라는 질문들은 매우 자연스럽다.
우리가 살펴볼 버전 ( 정석에 나와있는 ) 의 케일리 해밀턴 정리는 다음과 같다.
정석에 나와있는대로, 단위행렬 E 로 표기하자. ( 항등행렬 I 는 이미 1차변환에 대한 생각이 담겨있다고 하겠다. )
주어진 행렬 A 에 대해 , p = a + d ( trace ) 이고, q = ad - bc ( determinant ) 이면 A² - p A + q E = 0 이다.
따라서, 역은 다음과 같다.
주어진 행렬 A 에 대해, A² - p A + q E = 0 이면 p = a + d ( trace ) 이고, q = ad - bc ( determinant ) 이다.
( 주의 : 어떤 행렬방정식을 만족하는 행렬이 하나라는 뜻은 아니다. 오해 하지 말자. )
반례를 통해, 역이 성립하지 않는것을 보이자.
주어진 A = 5 E 에 대해, A² - 4 A - 5 E = 0 이지만, 4 가 a + d 는 아니다. 그러므로, 성립 X. 따라서, 역은 성립하지 않는다.
그렇다면 언제 성립할까?
결론부터 말하자면, 주어진 행렬이 단위행렬의 스칼라배가 아니라는 보장이 있으면, 역이 성립한다. 즉, A² - p A + q E = 0 이면 p = a + d ( trace ) 이고, q = ad - bc ( determinant ) 이다. 이말은 결국, 단위행렬의 스칼라배가 아닌 행렬에 대해서는 monic 2차 행렬방정식이 유니크함을 의미한다 !!!
(주의. 방정식에 대해 행렬이 유니크하다는 뜻은 아니다. 서로 다른 두 행렬이 같은 식을 갖을수도 있다. 간혹, 이부분을 잘못받아들이는 경우가 종종있다. 심지어 몇몇 고삐리문제집들 조차도... -_-a )
증명을 해보자.
어떤 A 가 단위행렬의 스칼라배, 즉, kE 라면, ( A - kE ) 에다가 임의의 스칼라 m 에 대해 , A - m E 를 곱해서 전개하면 무수히 많은 monic 2차 행렬방정식을 만들수 있다. 따라서, 단위행렬의 스칼라배인 행렬에 대해, 2차 방정식이 주어졌다고 해도, 그것이 케일리 해밀턴 정리로 주어진 식이라고는 보장할 수 없다.
그러나, A 가 kE 꼴이 아니라고 하고, A² - p A + q E = 0 라고 하자. 케일리 해밀턴 정리는 항상 성립하므로, A² - tr A + D E = 0 도 역시 참이다. ( tr = a + d , D = ad - bc )
두식을 빼서 양변을 A 와 E 로 분리해서 정리하면, A 가 E 의 스칼라배가 아니라는 조건으로 부터, 양쪽의 계수가 모두 0 이어야 한다는 결과를 얻는다. 그로부터, p = tr 이고, q = D 를 얻는다. 따라서, 역이 성립한다. 이것은 매우 놀라운 결과이다.
예를 들어보자.
A = ( a 1 ) 에 대해, A² - 4 A - 5 E = 0 가 성립한다고 하자. 이경우, A가 E의 스칼라배가 아니므로
( 0 b ) 주어진 식은 케일리 해밀턴 정리이고 계수는 각각 - trace 와 det 이다.
따라서, a+b = 4 이고, ab = -5 라는 단서를 얻게 된다.
A = ( 2 1 ) 에 대해, A² + p A + q E = 0 인 경우는 , A가 E의 스칼라배가 아니므로,
( 0 1 ) 케일리 해밀턴 정리에 의한 식 하나 밖에 없다. 즉, A² -3 A + 2 E = 0 외에는 없다.
그러나, A = a E 에 대해 A² - 4 A - 5 E = 0 가 성립한다고 할때, 주어진 식이 케일리 해밀턴 정리라는 보장은 없다. 왜냐면 그러한 식은 무수히 많기 때문이다. 특히, 이 경우 케일리 해밀턴 식이 아님을 알 수 있는데, 케일리 해밀턴 정리를 직접 쓰면 A² - 2a A + a² E = 0 꼴이 되어야 하는데, 주어진 식은 그와 다르기 때문이다. 여기서, a를 구하기 위해서는 주어진 식에 대입하면 된다. 그러면, 행렬방정식이 실방정식이 되고, 실방정식은 제로디바이저(영인자)가 없으므로, 간단히 해결된다. a = 5 또는 a = -1 이 된다.
[C언어] 문자열(string) , 문자열상수, 리터럴(literal)
COM2008. 6. 29. 19:01 |문자열 (string)
문자열은 char 형 1차원 배열이다. ( char형의 크기는 1byte 이다. )
문자열은 NULL 문자로 그 끝을 나타낸다.
NULL 문자는 1byte의 모든 비트, 즉 8비트가 모두 0 값이다. 즉, 0000 0000
escape 문자를 사용한 NULL 문자 기호는 \0 이다.
------------------------------------------------------------------------------------------------
문자열 상수 (string constant)
문자열상수는 " " 를 사용하여 나타낸다. 단일 문자는 ' ' 를 사용한다.
문자열이 겉보기에 단일문자만 가지고 있더라도 NULL 문자때문에 단일문자와는 다르다.
문자열의 크기에는 널문자가 포함된다.
예. "abc" <-- 크기가 4바이트인 문자열 상수
연속된 문자열 상수는 접합된다. (concatenation) , 이때 문자열 상수 사이의 공백은 무시된다.
즉, "abc" "def" 는 "abcdef" 가 된다.
문자열이 길어서 중간에 끊기는 것 때문에 인쇄문을 두번 쳐야 할때, 위의 테크닉을 이용하면 편리하다. 즉, 긴문자열을 여러개로 끊고 연속시키는 것이다.
예.
printf("This string is too much "
"long. So I split the string "
"to four segments then "
"it will be concatenated.");
--------------------------------------------------------------------------------------------------
문자열 상수의 특정위치 문자 역참조하기
문자열상수는 비록 이름은 없지만, 메모리 어딘가에 저장되고, 평가값이 그 시작주소 이므로, [] 연산자를 이용해 역참조하면, 문자열의 특정위치에 있는 문자를 택할수 있다.
즉, "ABCDEFG"[4] 와 같은 꼴로 쓰면 된다. "ABCDEDFG"[4] 는 'E' 이다.
앞에서 연속된 문자열 상수가 접합된다고 하였으므로, "AB""CDEFG"[4] 라고 해도 똑같다.
예.
#include<stdio.h>
int main(void){
int i;
for(i=0;("This is a string"" literal"[i])!='\0';i++){
putchar("This is"" a string literal"[i]);
}
return 0;
}
-----------------------------------------------------------------------------------------------
리터럴 (literal)
리터럴이란 "문자그대로" 라는 뜻이다.
In computer science, a literal is a notation for representing a fixed value in source code.
컴퓨터 사이언스에서, 리터럴은 "원시코드에 있는 어떠한 고정된 값"을 나타내기 위해 사용되는 용어이다.
원시 프로그램에서 어떠한 숫자 또는 기호로서 다른 데이터를 가리키는 역할을 하지 않고 그 자신이 바로 데이터로서 사용되는 것을 이른다.
예를들면, 어셈블러에서 LDA 100 이라고 하면, A 레지스터에 100번지에 있는 내용을 LOAD 하라는 것이지만,
LDA #100 이라고 하면, A 레지스터에 100 이라는 값을 넣으라는 것이 된다.
LDA 100 에서 LDA 는 load 라는 기능을 의미하고, 100은 100 이라는 숫자 자신이 아닌 번지수로 사용이 된 반면,
LDA #100 에서 #은 그 뒤에 있는 것을 리터럴로 취급하라는 표시 인데, 즉, 뒤의 100 이라고 하는 것은 그냥 100 그 자체일 뿐이다.
----------------------------------------------------------------------------------------------------
상수(constants)
고정된 값을 나타내는 또다른 개념중에 상수(constant)가 있는데, 리터럴은 상수하고는 조금 다른 개념이다.
상수는 수학으로 부터 비롯된 개념으로, 값이 변하지 않는 양을 말한다. 이것은 매우 포괄적인 개념이다.
아무튼 수학의 개념을 물려받아, 컴퓨터사이언스에서도 상수라는 개념을 쓰는데, 이것은 실제로는 값이 변하지 않는 변수이다.
그렇다고 하더라도, 컴퓨터 사이언스의 상수는 수학의 상수와 본질적으로 다르지 않은데, 수학에서, 변환에 대한 약간의 지식만 있으면 간단하게 이해할 수 있다.
가령, 다항 함수공간을 예로 들면, 각 함수에서 0차 항을 포함한 계수들은 값이 고정된 상수이지만, 그러한 함수들을 모아놓은 함수공간에서는, 계수들(0차항포함)이 각종 변환에서 오히려 변수역할을 한다는 것을 알수 있다. 일종의 듀얼리티 같은건데, 아무튼 하려는 짓이 무엇이냐에 따라 상수들도 변할 수 있다.
좀더 느낌이 오게 구체적으로 설명하자면... 이차함수 y = ax^2 + bx + c 에서 x 는 독립변수, y는 종속변수 이고, a,b,c 는 값이 고정된 상수들 이지만, 이차함수를 좨다 모아놓은 집합에서 임의의 원소 하나를 고르는 것은 (a,b,c) -> f 인 매핑이다. 즉, a,b,c 가 세개의 독립변수가 된다.
즉, 크게볼때 상수와 변수는 우리의 관심대상이 그것을 고정시켰느냐 아니냐의 차이일 뿐이다.
---------------------------------------------------------------------------------------------------
리터럴과 상수의 구분
이제 위와 같은 개념으로 부터 상수와 리터럴을 구별을 해보자.
CONST x := "abc"
CONST y := 10
위와 같이 x 에 문자열 abc 를 값이 변하지 않도록 고정시켜 배정했다고 치자.
(이렇게 고정되게 선언하는 구문은 프로그래밍 언어마다 차이가 있고, 우리는 특정 프로그래밍 언어에 대한 이야기를 하는 것이 아님에 유의한다.)
아무튼, 여기서 abc 라고 하는 것은 그냥 abc 자체를 나타내므로 리터럴이다.
반면, x 는 x 자체가 아니다. abc 라는 데이터를 가리키는 녀석이다. 즉, 리터럴이 아니다.
다시말해, x는 상수이고, abc는 리터럴이다. 특히 스트링 리터럴 이라고 한다.
y는 상수이고, 10은 리터럴이다. 특히, 숫자 리터럴 이라고 한다.
그런데, 리터럴들도 값이 변하지 않는다는 의미에서는 상수라고 할 수 있다.
실제로, 많은 고급언어에서 스트링 리터럴을 스트링 상수 라고 부른다.
즉, 리터럴이라는 개념은 상수라는 개념의 부분집합이다.
In contrast to literals, variables or constants are symbols that can take on one of a class of fixed values, the constant being constrained not to change.
Literals are often used to initialize variables.
위에서 보듯이, 리터럴은 변수를 초기화 하는데 자주 사용된다.
리터럴도 값이 변하지 않는다는 측면에서 상수이므로, 리터럴과 상수를 구분하는 다른 크라이테리어인 이름에 대해 생각해 보자.
리터럴은 상수와 마찬가지로 메모리 어딘가에 값이 변하지 않도록 저장이 되지만, 이름이 없다.
가령, 다음과 같이 두개의 문장이 있다고 하자.
1: CONST a : = 10
2: "abc"
해당 프로그래밍언어의 컴파일러 (혹은 인터프리터)는 a 라는 메모리 공간을 확보하고, 거기에 리터럴 10 을 집어넣는다. a 는 a 자체가 데이터가 아니라 다른 데이터, 즉, 10을 나타내는 이름이다.
두번째 문장의 경우, 문자열 abc 를 메모리 어딘가에 저장한다. 그러나 이것은 따로 이름이 없다. 그저 그 자체로 abc 일뿐이다. 굳이 말하자면, 그 자신이 이름이며 동시에 데이터이다. 물론 주소는 갖는다.
-----------------------------------------------------------------------------------------------
변수,상수,리터럴의 포함관계
변수는 변수명, 주소, 공간, 형식(읽기, 쓰기 등) 등의 요소를 갖는다.
상수는 변수에서 쓰기연산이 금지된 것이다.
리터럴은 쓰기연산이 금지되고, 변수명도 없는 것이다.
-----------------------------------------------------------------------------------------------
문자열상수의 평가값
컴파일러는 문자열 상수 (또는 리터럴) 를 보면, 메모리 어딘가에 해당 문자열을 위한 공간을 마련하여 저장한다. 이것은 리터럴이므로 별도의 이름을 갖지 않는다. 대신 어딘가에 저장되어있으므로, 주소는 갖는다.
문자열 상수의 평가값이 바로 문자열의 시작주소이다. 즉, 평가값은 const char* 형이고, 따라서, char* 형 변수에 배정할수 있다. pinrtf() 함수의 프로토타입에서 문자열 상수를 인자로 받을때, const char* 를 썼던것을 기억하자.
예.
#include<stdio.h>
int main(void)
{
char *p;
p = "Hello!\n"; // 메모리 어딘가에 문자열을 저장하고, 그 시작주소를 p가 포인팅하도록 한다.
printf(p); // p 가 포인팅 하는 곳에서 시작하여 NULL문자를 만날때까지 문자를 인쇄한다.
return 0;
}
문자열은 문자들의 배열이므로 위에서 char* 형으로 선언한것은 그냥 char형 배열로 선언해도 된다.
char str[] = "abc" ; 이것은 배열의 초기화 char str[] = { 'a' , 'b' , 'c' , '\n' }; 와 동일하다.
널스트링 (null string)
NULL 스트링은 아무것도 없는 스트링으로, 결과적으로 스트링의 끝을 알리는 NULL 문자만을 가지고 있다.
"" 은 널스트링이고, " " 은 공백을 가지고 있는 스트링으로 둘은 다르다.
예제. 널스트링의 출력
printf("You've got %d point%s.\n",pt,((pt==1)?"":"s"));
위 문장은, 점수가 1점이 아니면, 복수형인 points 를 쓴다. 반면, 1점이면, s대신 널스트링이 출력되어 point와 마침표사이에 공백없이 인쇄된다.
[WinXP] 탐색기 2개의 편리한 작업 방법
COM2008. 6. 18. 02:20 |
윈도우키+E 를 누르면 탐색기가 되는데, 연속 두번 눌러서, 탐색기 두개를 띄운다.
작업표시줄(화면하단의 바) 에대고 우클릭한다음 가로 바둑판식 배열, 또는 세로 바둑판식 배열을 선택한다.
이것이 본인이 가장 선호하는 작업방식.
[윈XP] Alt , Shitf
COM2008. 6. 17. 23:24 |Alt + 좌, 우 : 뒤로, 앞으로
Shift + 더블클릭 폴더 : 탐색기로...
2008/06/08 하늘
Misc.2008. 6. 8. 15:49 |
오후 세시반의 하늘이 저녁처럼 어둡다. 일년에 200일 이상 이렇게 비가 온다 해도, 하늘색을 하늘색이라 말할까? 누군가 그랬다. 하늘색은 하늘에 있을때 가장 예쁘다고. 지금도 하늘색은 하늘에 있어 하늘색이 참 이쁘다. 흙탕물을 풀어놓은것 처럼.

수묵담채화 같다.
-------------------------------------
트랙백이 뭔지 모르는 사람들의 상식증대 차원에서 간단히 설명하자면... 트랙백이란, "남의 글에 답글을 다는것" 이긴 한데, 남의 게시판에 직접 답글을 남기는게 아니라, 답글 자체는 내 블로그에 보관하고, 링크만 남기는 방식이라고 할 수 있겠다.
-------------------------------------
사용법은 아주 간단하다.
1. 답글을 달고자 하는 글 ( 대상글 이라 하자 ) 의 트랙백 주소를 알아낸다.
2. 답글을 내 블로그에다 쓴다.
3. 내 답글을 대상글의 트랙백주소로 보낸다.
4. 대상글에 내 답글이 달린다.
----------------------------------------
그럼 이제 답글을 달때는 대상글의 트랙백 주소만 알면 되는거다. 근데 어떻게?
네이버 블로그나 이런데 보면, " 엮인글 쓰기 " , " 트랙백" 뭐 이런 게 달려있는데가 있는데, 보통 거길 클릭하면, 트랙백 주소를 보여준다. 그리고, "주소복사" 같은 버튼이 있어서 누르면 자동으로 주소를 복사해 놓아서, 붙여넣기 해서 쓸수있게 해준다. 아니면 그냥 마우스로 드래그해서 복사해도 된다.
내 블로그는 글 하단에 "답글쓰기" 라는 버튼을 누르면, 트랙백주소가 뜨는데, 마우스로 트랙백주소를 클릭하면 복사가 된다.
참고로, 글쓴이가 트랙백을 허용 안하면, 트랙백 주소를 가르쳐주지 않으므로, 트랙백을 걸수가 없다. 이럴땐 그냥 댓글이나 달자.
------------------------------------------
트랙백 주소는 알았는데, 트랙백은 어떻게 보내나?
자신의 블로그에서 작성한 글에서 트랙백 보내기 등의 버튼을 클릭하면, 대상글의 트랙백 주소를 입력하라고 나온다. 거기에 아까 복사해둔 대상글의 트랙백주소를 붙여넣기하면 된다.
답글을 굳이 새로 쓰지 않더라도, 이전에 내가 써놓은 글이 대상글과 연관이 있거나 해서, 글쓴이 혹은 그 글을 보는 사람들에게 노출시키고 싶을때에도 트랙백을 걸면 된다.
그래서 보통, 답글이라는 말보다는 엮인글 내지는 관련글 이라는 표현을 주로 쓴다.
[역학] 왜 우리는 달의 한면만 보게 될까? ( Tidal Locking )
Physics/Math./Mech./Gen. Relativity2008. 6. 1. 20:37 |아무튼, 그때 물상 선생님한테, 그 이유에 대해 물었을때 돌아온 답은 역시 교과서 그대로였다. 달의 자전주기와 공전주기가 같아서 라고... 나는 즉각, 어떻게 그것이 가능하냐고 물었는데, 역시나 되돌아온 대답은 "관찰의 결과" 그렇기 때문이라는 것이다.
여기서 응당 이어져야 할 의문은 " 그럼 어떻게 그것은 지속가능한 것입니까? " 라고 할 수 있겠다. 왜냐하면, 달의 수많은 크레이터 들이 보여주듯이, 운석의 충돌이나 어떠한 우주적인 사건에 의해 달의 회전에는 변화가 생길수 있기 때문이다. 그렇게 따져 물었어야 했는데, 그땐 그냥 돌아섰다. 아무튼 끝까지 미심쩍어서 쉬이 발길이 돌아서지 못하던 때에 돌아온 대답은 의외로 종교적이었다.
지구가 그만큼 특별한거라고... -_-;;;
그.러.나.
현재 역학을 공부하다가 tidal force 에 대해 공부하게 되면서 알게 된건데... 지구와 달 만의 현상이 아니란거다. -_- 아주 보편적인 현상이며 오랜 시간이 지나면 이벤추얼리 대부분의 돌고도는 위성 행성 별 등이 서로 같은 면만 보게 된다. 이를 타이들 락킹 이라고 한다.
아래 위키에서 퍼온 설명인데, 보면 알겠지만, locked 된 애들 무지 많다. -_- 달만 그런게 아니다. 그리고 아직 locked 안된 애들도, 대체로 고정이 되는 중인거다.
자세한 설명은 아래에 나와 있다. 궁금한 사람은 꼭 자세히 읽어보도록 하자. 어느정도 이해할려면 적어도 종이와 연필을 들고 그림 몇장 정도는 그려야 할 것이다. 다음에 기회가 되면 그림과 함께 풀어서 설명을 해보도록 하겠다.
Tidal Locking
Tidal locking occurs when the gravitational gradient makes one side of an astronomical body always face another
; for example, one side of the Earth's Moon always faces the Earth.
A tidally locked body takes just as long to rotate around its own axis as it does to revolve around its partner. This synchronous rotation causes one hemisphere constantly to face the partner body.
Usually, only the satellite becomes tidally locked around the larger planet, but if the difference in mass between the two bodies and their physical separation is small, both may become tidally locked to the other, as is the case between Pluto and Charon. This effect is employed to stabilize some artificial satellites.
Mechanism of Tidal Locking
The change in rotation rate necessary to tidally lock a body B to a larger body A is caused by the torque applied by A's gravity on bulges it has induced on B by tidal forces.
Tidal bulges
A's gravity produces a tidal force on B which distorts its gravitational equilibrium shape slightly so that it becomes stretched along the axis oriented toward A, and conversely, is slightly compressed in the two perpendicular directions.
These distortions are known as tidal bulges.
When B is not yet tidally locked, the bulges travel over its surface, with one of the two "high" tidal bulges traveling close to the point where body A is overhead.
For large astronomical bodies which are near-spherical due to self-gravitation, the tidal distortion produces a slightly prolate spheroid or ellipsoid.
Smaller bodies also experience distortion, but this distortion is less regular.
Bulge dragging
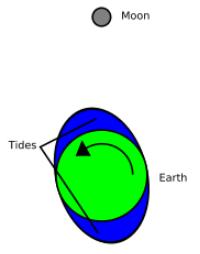
The material of B exerts resistance to this periodic reshaping caused by the tidal force.
In effect, some time is required to reshape B to the gravitational equilibrium shape, by which time the forming bulges have already been carried some distance away from the A-B axis by B's rotation.
Seen from a vantage point in space, the points of maximum bulge extension are displaced from the axis oriented towards A.
If B's rotation period is shorter than its orbital period, the bulges are carried forward of the axis oriented towards A in the direction of rotation, whereas if B's orbital period is shorter the bulges lag behind instead.
Resulting torque
Since the bulges are now displaced from the A-B axis, A's gravitational pull on the mass in them exerts a torque on B.
The torque on the A-facing bulge acts to bring B's rotation in line with its orbital period, while the "back" bulge which faces away from A acts in the opposite sense.
However, the bulge on the A-facing side is closer to A than the back bulge by a distance of approximately B's diameter, and so experiences a slightly stronger gravitational force and torque.
The net resulting torque from both bulges, then, is always in the direction which acts to synchronize B's rotation with its orbital period, leading eventually to tidal locking.
Orbital changes
The angular momentum of the whole A-B system is conserved in this process, so that when B slows down and loses rotational angular momentum, its orbital angular momentum is boosted by a similar amount (there are also some smaller effects on A's rotation).
This results in a raising of B's orbit about A in tandem with its rotational slowdown.
For the other case where B starts off rotating too slowly, tidal locking both speeds up its rotation, and lowers its orbit.
Locking of the larger body
The tidal locking effect is also experienced by the larger body A, but at a slower rate because B's gravitational effect is weaker due to B's smaller size.
For example, the Earth's rotation is gradually slowing down because of the Moon, by an amount that becomes noticeable over geological time in some fossils.
For similar sized bodies the effect may be of comparable size for both, and both may become tidally locked to each other.
The dwarf planet Pluto and its satellite Charon are good examples of this— Charon is only visible from one hemisphere of Pluto and vice versa.
Tidal acceleration
Tidal acceleration is an effect of the tidal forces between an orbiting natural satellite (i.e. a moon), and the planet (called the primary) that it orbits.
It causes a gradual recession of a satellite in a prograde orbit away from the primary, and a corresponding slowdown of the primary's rotation.
The process eventually leads to tidal locking of first the smaller, and later the larger body.
The Earth-Moon system is the best studied case.
The similar process of tidal deceleration occurs for satellites that have an orbital period that is shorter than the primary's rotation period, or that orbit in a retrograde direction.
Effects of moon's gravity
Because the Moon's mass is a considerable fraction of that of the Earth (about 1:81), the two bodies can be regarded as a double planet system, rather than as a planet with a satellite.
The plane of the Moon's orbit around the Earth lies close to the plane of the Earth's orbit around the Sun (the ecliptic), rather than in the plane perpendicular to the axis of rotation of the Earth (the equator) as is usually the case with planetary satellites.
The mass of the Moon is sufficiently large and it is sufficiently close to raise tides in the Earth:
the matter of the Earth, in particular the water of the oceans, bulges out along both ends of an axis passing through the centers of the Earth and Moon.
The average tidal bulge closely follows the Moon in its orbit, and the Earth rotates under this tidal bulge in just over a day.
However, the rotation drags the position of the tidal bulge ahead of the position directly under the Moon.
As a consequence, there exists a substantial amount of mass in the bulge that is offset from the line through the centers of the Earth and Moon.
Because of this offset, a portion of the gravitational pull between Earth's tidal bulges and the Moon is perpendicular to the Earth-Moon line, i.e. there exists a torque between the Earth and the Moon.
This accelerates the Moon in its orbit, and decelerates the rotation of the Earth.
So the result is that the mean solar day, which is nominally 86400 seconds long, is actually getting longer when measured in SI seconds with stable atomic clocks.
The small difference accumulates every day, which leads to an increasing difference between our clock time (Universal Time) on the one hand, and Atomic Time and Ephemeris Time on the other hand: see ΔT.
This makes it necessary to insert a leap second at irregular intervals.
If other effects were ignored, tidal acceleration would continue until the rotational period of the Earth matched the orbital period of the Moon.
At that time, the Moon would always be overhead of a single fixed place on Earth.
Such a situation already exists in the Pluto-Charon system.
However, the slowdown of the Earth's rotation is not occurring fast enough for the rotation to lengthen to a month before other effects make this irrelevant:
About 2.1 billion years from now, the continual increase of the Sun's radiation will cause the Earth's oceans to boil away, removing the bulk of the tidal friction and acceleration.
Even without this, the slowdown to a month-long day would still not have been completed by 4.5 billion years from now when the Sun will evolve into a red giant and likely destroy both the Earth and Moon.
Tidal acceleration is one of the few examples in the dynamics of the solar system of a so-called secular perturbation of an orbit, i.e. a perturbation that continuously increases with time and is not periodic.
Up to a high order of approximation, mutual gravitational perturbations between major or minor planets only cause periodic variations in their orbits, that is, parameters oscillate between maximum and minimum values.
The tidal effect gives rise to a quadratic term in the equations, which leads to unbounded growth.
In the mathematical theories of the planetary orbits that form the basis of ephemerides, quadratic and higher order secular terms do occur, but these are mostly Taylor expansions of very long time periodic terms.
The reason that tidal effects are different is that unlike distant gravitational perturbations, friction is an essential part of tidal acceleration, and leads to permanent loss of energy in the form of heat.
Angular momentum and energy
The gravitational torque between the Moon and the tidal bulge of the Earth causes the Moon to be accelerated in its orbit, and the Earth to be decelerated in its rotation.
As in any physical process, total energy and angular momentum are conserved.
Effectively, energy and angular momentum are transferred from the rotation of the Earth to the orbital motion of the Moon.
The Moon moves farther away from the Earth, so its potential energy (in the Earth's gravity well) increases.
It stays in orbit, and from Kepler's 3rd law it follows that its velocity actually decreases, so the tidal acceleration of the Moon causes an apparent deceleration of its motion across the celestial sphere.
Although its kinetic energy decreases, its potential energy increases by a larger amount.
The Moon's orbital angular momentum also increases.
The rotational angular momentum of the Earth decreases and consequently the length of the day increases.
The net tide raised on Earth by the Moon is dragged ahead of the Moon by Earth's much faster rotation.
Tidal friction is required to drag and maintain the bulge ahead of the Moon, and it dissipates the excess energy of the exchange of rotational and orbital energy between the Earth and Moon as heat.
If the friction and heat dissipation were not present, the Moon's gravitational force on the tidal bulge would rapidly (within two days) bring the tide back into synchronization with the Moon, and the Moon would no longer recede.
Most of the dissipation occurs in a turbulent bottom boundary layer in shallow seas such as the European shelf around the British Isles, the Patagonian shelf off Argentina, and the Bering Sea.
A tidal bulge (called an equilibrium tide) does not really exist on Earth because the continents break up the tide when they pass under the Moon.
Oceanic tides actually rotate around each ocean basin as vast gyres around several amphidromic points where no tide exists.
The Moon pulls on each individual undulation as Earth rotates—some undulations are ahead of the Moon, others are behind it, while still others are on either side.
The equilibrium tide in the shape of a prolate spheroid that actually does exist for the Moon to pull on is the net result of integrating the actual undulations over all the world's oceans.
Earth's net equilibrium tide has an amplitude of only 3.23 cm, which is totally swamped by oceanic tides that can exceed one metre.
Historical evidence
This mechanism has been working for 4.5 billion years, since oceans first formed on the Earth.
There is geological and paleontological evidence that the Earth rotated faster and that the Moon was closer to the Earth in the remote past.
Tidal rhythmites are alternating layers of sand and silt laid down offshore from estuaries having great tidal flows.
Daily, monthly and seasonal cycles can be found in the deposits.
This geological record is consistent with these conditions 620 million years ago:
the day was 21.9±0.4 hours, and there were 13.1±0.1 synodic months/year and 400±7 solar days/year.
The length of the year has remained virtually unchanged during this period because no evidence exists that the constant of gravitation has changed.
The average recession rate of the Moon between then and now has been 2.17±0.31 cm/year, which is about half the present rate.
Quantitative description of the Earth-Moon case
The motion of the Moon can be followed with an accuracy of a few centimeters by lunar laser ranging (LLR).
Laser pulses are bounced off mirrors on the surface of the moon, emplaced during the Apollo missions of 1969 to 1972 and by Lunokhod 2 in 1973.
Measuring the return time of the pulse yields a very accurate measure of the distance.
These measurements are fitted to the equations of motion.
This yields numerical values for the parameters, among others the secular acceleration.
From the period 1969–2001, the result is:
+3.84 ± 0.07 m/cy in distance
This is consistent with results from satellite laser ranging (SLR). This is a similar technique applied to artificial satellites orbiting the Earth.
This yields an accurate model for the gravitational field of the Earth, including that of the tides.
This can be used to predict its effect on the motion of the Moon, which yield very similar results.
Finally, ancient observations of solar eclipses give a fairly accurate position for the Moon at that moment.
Studies of these give results consistent with the value quoted above.
The other consequence of the tidal acceleration is the deceleration of the rotation of the Earth.
The rotation of the Earth is somewhat erratic on all time scales (from hours to centuries) due to various causes.
The small tidal effect can not be observed in a short period but the cumulative effect of the Earth's actual daily rotation occurring in less than 24 hours as measured on a stable clock (ephemeris time, atomic time) even a few milliseconds every day, becomes readily noticeable in a few centuries.
Since some event in the remote past, more days and hours have passed (as measured in full rotations of the Earth) (Universal Time) than as measured with stable clocks calibrated to the present, longer length of the day (ephemeris time).
This is known as ΔT. Recent values can be obtained from the International Earth Rotation and Reference Systems Service (IERS).
A table of the actual length of the day in the past few centuries is also available.
From the observed acceleration of the Moon, the corresponding change in the length of the day can be computed:
+2.3 ms/cy
However, from historical records over the past 2700 years the following average value is found:
+1.70 ± 0.05 ms/cy
The corresponding cumulative value is a parabola having a coefficient of T² (time in centuries squared) of:
ΔT = +31 s/cy²
Counter to the tidal deceleration of the Earth, there is a mechanism that is in fact accelerating the rotation.
The Earth is not a sphere, but rather an ellipsoid that is flattened at the poles.
SLR has shown that this flattening is decreasing.
The explanation is, that during the ice age large masses of ice collected at the poles, and depressed the underlying rocks.
The ice mass started disappearing over 10000 years ago, but the Earth's crust is still not in hydrostatic equilibrium and is still rebounding (the relaxation time is estimated to be about 4000 years).
As a consequence, the polar diameter of the Earth increases, and since the mass and density remain the same, the volume remains the same;
therefore the equatorial diameter is decreasing.
As a consequence, mass moves closer to the rotation axis of the Earth.
This means that its moment of inertia is decreasing.
Because its total angular momentum remains the same during this process, the rotation rate increases.
This is the well-known effect of a spinning figure skater who spins ever faster as she retracts her arms.
From the observed change in the moment of inertia the acceleration of rotation can be computed:
the average value over the historical period must have been about −0.6 ms/cy .
This largely explains the historical observations.
Rotation-Orbit resonance
Finally, in some cases where the orbit is eccentric and the tidal effect is relatively weak, the smaller body may end up in an orbital resonance, rather than tidally locked.
Here the ratio of rotation period to orbital period is some well-defined fraction different from 1:1.
A well known case is the rotation of Mercury—locked to its orbit around the Sun in a 3:2 resonance.
Final configuration
There is a tendency for a moon to orient itself in the lowest energy configuration, with the heavy side facing the planet.
Irregularly shaped bodies will align their long axis to point towards the planet.
Both cases are analogous to how a rounded floating object will orient itself with its heavy end downwards.
In many cases this planet-facing hemisphere is visibly different from the rest of the moon's surface.
The orientation of the Earth's moon might be related to this process.
The lunar maria are composed of basalt, which is heavier than the surrounding highland crust, and were formed on the side of the moon on which the crust is markedly thinner.
The Earth-facing hemisphere contains all the large maria.
The simple picture of the moon stabilising with its heavy side towards the Earth is incorrect, however, because the tidal locking occurred over a very short timescale of a thousand years or less, while the maria formed much later.
Earth's Moon
The Moon's rotation and orbital periods are both just under 4 weeks, so no matter when the Moon is observed from the Earth the same hemisphere of the Moon is always seen.
The far side of the Moon was not seen in its entirety until 1959, when photographs were transmitted from the Soviet spacecraft Luna 3.
Despite the Moon's rotational and orbital periods being exactly locked, we may actually observe about 59% of the moon's total surface with repeated observations from earth due to the phenomena of librations and parallax.
Librations are primarily caused by the Moon's varying orbital speed due to the eccentricity of its orbit: this allows us to see up to about 6° more along its perimeter.
Parallax is a geometric effect : at the surface of the Earth we are offset from the line through the centers of Earth and Moon, and because of this we can observe a bit (about 1°) more around the side of the Moon when it is on our local horizon.
Moons
Most significant moons in the Solar System are tidally locked with their primaries, since they orbit very closely and tidal force increases rapidly (as a cubic) with decreasing distance.
Notable exceptions are the irregular outer satellites of the gas giant planets, which orbit much further away than the large well-known moons.
Pluto and Charon are an extreme example of a tidal lock. Charon is a relatively large moon in comparison to its primary and also has a very close orbit. This has made Pluto also tidally locked to Charon.
In effect, these two celestial bodies revolve around each other (their mass center lies outside of Pluto) as if joined with a rod connecting two opposite points on their surfaces.
The tidal locking situation for asteroid moons is largely unknown, but closely-orbiting binaries are expected to be tidally locked, as well as, obviously, contact binaries.
Planets
Until radar observations in 1965 proved otherwise, it was thought that Mercury was tidally locked with the Sun.
Instead, it turned out that Mercury has a 3:2 spin-orbit resonance, rotating three times for every two revolutions around the Sun
; the eccentricity of Mercury's orbit makes this resonance stable.
The original reason astronomers thought it was tidally locked was because whenever Mercury was best placed for observation, it was always at the same point in its 3:2 resonance, so showing the same face, which would be also the case if it were totally locked.
A curious aspect of Venus' orbit and rotation periods is that the 583.92-day interval between successive close approaches to the Earth is almost exactly equal to 5 Venusian solar days (precisely, 5.001444 of these), making approximately the same face visible from Earth at each close approach.
Whether this relationship arose by chance or is the result of some kind of tidal locking with the Earth is unknown.
Stars
Close binary stars throughout the universe are expected to be tidally locked with each other, and extrasolar planets that have been found to orbit their primaries extremely closely are also thought to be tidally locked to them.
An unusual example, confirmed by MOST, is Tau Boötis, a star tidally locked by a planet. The tidal locking is almost certainly mutual.


As can be seen, even knowing the size and density of the satellite leaves many parameters that must be estimated (especially w, Q, and , μ ), so that any calculated locking times obtained are expected to be inaccurate, to even factors of ten.
Further, during the tidal locking phase the orbital radius a may have been significantly different from that observed nowadays due to subsequent tidal acceleration, and the locking time is extremely sensitive to this value.
Since the uncertainty is so high, the above formulas can be simplified to give a somewhat less cumbersome one.
By assuming that the satellite is spherical, k_2 << 1 , Q = 100, and it is sensible to guess one revolution every 12 hours in the initial non-locked state (most asteroids have rotational periods between about 2 hours and about 2 days)
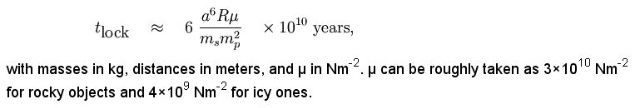
Note the extremely strong dependence on orbital radius a.
For the locking of a primary body to its moon as in the case of Pluto, satellite and primary body parameters can be interchanged.
One conclusion is that other things being equal (such as Q and μ), a large moon will lock faster than a smaller moon at the same orbital radius from the planet because m_s , grows much faster with satellite radius than R.
A possible example of this is in the Saturn system, where Hyperion is not tidally locked, while the larger Iapetus, which orbits at a greater distance, is.
This is not clear cut because Hyperion also experiences strong driving from the nearby Titan, which forces its rotation to be chaotic.
List of known tidally locked bodies
<< Solar System >>
Locked to the Sun
* Mercury (in a 3:2 rotation:orbit resonance)
Locked to the Earth
* Moon
Locked to Mars
* Phobos
* Deimos
Locked to Jupiter
* Metis
* Adrastea
* Amalthea
* Thebe
* Io
* Europa
* Ganymede
* Callisto
Locked to Saturn
* Pan
* Atlas
* Prometheus
* Pandora
* Epimetheus
* Janus
* Mimas
* Enceladus
* Telesto
* Tethys
* Calypso
* Dione
* Rhea
* Titan
* Iapetus
Locked to Uranus
* Miranda
* Ariel
* Umbriel
* Titania
Locked to Neptune
* Proteus
* Triton
Locked to Pluto
* Charon (Pluto being itself locked to Charon)
<< Extra-solar >>
* Tau Boötis is known to be locked to the close-orbiting giant planet Tau Boötis Ab[citation needed]
Bodies likely to be locked
<< Solar System >>
Based on comparison between the likely time needed to lock a body to its primary, and the time it has been in its present orbit (comparable with the age of the Solar System for most planetary moons), a number of moons are thought to be locked.
However their rotations are not known or not known enough.
These are:
Probably locked to Saturn
* Daphnis
* S/2004 S 6
* S/2004 S 4
* S/2004 S 3
* Methone
* Pallene
* Helene
* Polydeuces
Probably locked to Uranus
* Cordelia
* Ophelia
* Bianca
* Cressida
* Desdemona
* Juliet
* Portia
* Rosalind
* Cupid
* Belinda
* Perdita
* Puck
* Mab
* Oberon
Probably locked to Neptune
* Naiad
* Thalassa
* Despina
* Galatea
* Larissa
Probably locked to other dwarf planets and minor planets
Numerous asteroid and TNO moons are expected to be locked to their primaries. However, in the absence of direct observation reliable candidates are difficult to verify. While locking timescales can be estimated, the age of the primary+satellite system is difficult to gauge; most are thought to be the results of collisions in the last few hundred million years.
<< Extra-solar >>
* Gliese 581 c may be tidally locked to its parent star Gliese 581.

 메튜엔워커-수리물리.djvu
메튜엔워커-수리물리.djvu