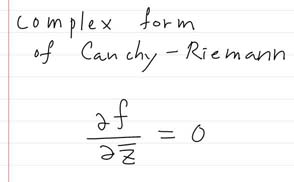
컴플렉스 플레인과 유클리디언 플레인의 차이를 통해 컴플렉스 플레인이 뭔지를 살펴보자.


메트릭 스페이스로만 보자면 컴플렉스 플레인이나 유클리디언 R² 플레인이나 똑같다. metric인 norm 도 같은걸 쓴다.


algebraic structure 로서 살펴보면, 우선 addition 도 같은 걸 쓴다. 즉, (a,b) + (c,d) = (a+c,b+d)
그러니까 이상태에서 VS over R 을 구성하면 R² 나 C 나 완전하게 똑같은 VS 이다.


결국, 차이는 복소수 곱셈뿐이다. 그러니까 R² 에  (a,b) (c,d) = ( ac - bd , ad + bc ) 라는 곱셈을 추가한 algebraic structure 가 복소평면이라고 할수있다.


복소수의 곱셈을 위처럼 먼저 정의하고, 허수단위 i 를 ( 0, 1 ) 에 대한 special name 정도로 불러줘도 좋고, 반대로 i 를 특수하게 먼저정의하고, 리니어리티 따위로 곱셈을 정의해도 된다.


요컨대, C 는  R² 에 곱셈연산이 하나 추가된 , 즉, R² 의 스페셜케이스이므로,  R² 상에서 성립하는 제너럴한 정리들은 그대로 쓸 수 있다.

즉, 2차원 회전행렬이라던가 , 면적분에 대한 그린정리 라던가 하는걸 다 써도 된다는 소리다.

느린 두뇌회전을 가지고 있는 사람의 하루 공부량은 보잘것 없이 적다.
그래도 measure zero 만 아니면 되는거다.

하루에 모래알 하나씩 모아서, 태산을 쌓는것과 같은거다. 하루하루는 보잘것 없지만, 모이면 언젠가 힘이 되겠지...

그...근데, 너무 늦다 ㅠㅠ. 뭐 중간에 딴짓을 너무 많이 하는 것도 사실이지만... 목요일부터 내내 오늘까지 시간이 있었는데, 복소숙제 하나를 못했다. 미쳐버리겠네... 해석숙제도 나왔는데... 대수도 링 봐야되는데.... 헐...

지수함수(exponential funcion)는 주기가 허수( 2 π i )인 주기함수(periodic funtion)이다.

for any complex number z ,

exp[ z + 2 π i ] =  exp [ z ]

therefore, exp[ z ] is periodic , with the period  2 π i

이번학기에 다변수함수론 Calculus on Manifold ...

결국, 이사람이 그사람이고 , 그사람이 이사람이고, ...
그코시가 이코시이고 그가우스가 이가우스고, ...가우스 이새끼는 안나오는데가 없다. -_-;;; 가우스님 죄송.

아, 능력자들...

비트단위 연산 & , | , ^ , << , >> 따위는 피연산자가 정수형으로 제한되어있다.

따라서, 단순히 마스크 만들고 & 연산해서 특정위치의 비트를 알아내는 방법은 먹히지 않는다.
문제는 실수형 타입에 비트연산자들이 접근할수 없다는 것이므로, 이것만 해결하면 된다.

간단한 방법은, union(공용체) 를 사용하는 것이다.

공용체에 실수형 멤버와 정수형 멤버를 같이 선언해서, 같은 메모리를 실수형으로도, 정수형으로도 사용할 수 있게 만들면 된다. 그래서, 배정은 실수 멤버에 하고, 비트연산은 정수형 멤버로 하면 간단히 해결된다.

이와같은 방법을 사용하면, 실수데이타의 비트 시퀀스를 볼수있고, 비트처리를 할수도있다.

---------------------------------------------------------------------------------------------------

다음의 첨부파일은 실수형 데이터의 비트단위 출력 프로그램이다. 코드는 위에서 말한것처럼 공용체와 비트필드를 사용하여 작성되었다.

realdata_bit.exe

프로그램은 입력된 실수 데이터를 float 형과 double 형으로 비트 시퀀스를 찍는다.
처음엔, 바이트 단위로 묶어서 출력하고,
두번째는, 의미론적 자료구조를 반영해서 찍는다.
실수 데이터의 부동소수점 표현에 관한 표준규약은 IEEE 754 에 포함되어있다.

간단히 언급만 하자면, 부호필드, 지수필드, 가수(mantissa) 필드 이렇게 순서대로 셋으로 쪼개진다.

단, 0.0 은 그냥 모든 bit 값을 0 으로 하는 것으로 정한다.

부호 필드는 float , bouble 둘다 최상위 1비트 이다.
0: non-negative, 1: negative

지수 필드는 float 의 경우 그 다음의 상위 8 비트이며, double의 경우 11비트 이다.
지수 필드의 경우, 크기 비교 등의 이점을 위해, 지수 바이어스 (Exponent Bias) 를 더해서 저장한다.
참고로, single precision bias 는 2^(8-1) -1 = 127 = 0111 1111 이고, double precision bias 는 2^(11-1) - 1 = 1023 = 011 1111 1111 이다.

지수 필드에, 해당 바이어스를 추가해서 더하면, 지수필드의 첫번째 비트(Exp sign bit) 가 오히려 + 가 1 이 된다.

가수필드는 float 의 경우  23비트, double의 경우 53비트 이다. (double 에서 float 로 캐스팅될땐 자료의 손실이 발생할 수 있다.)
가수, 지수, 밑 따위는 모두 2진수 기준이다.
가수필드 저장시 1 + m1 x 1/2  + m2 x 1/4 + ...  식으로 될때, 1 은 생략하고 m1,m2,m3,... 부분만 저장한다. (이진수 이므로, m1, m2, ... 모두 0 또는 1 로, 해당 2^-k 자리 값이 있으면 1 없으면 0 이다.)
가령, float 의 23bit mantissa 필드의 경우, 1.8125 = 1 + 1/2 + 1/4 + 0 + 1/16      =>   110 1000 0000 0000 0000 0000 와 같이 된다.

요약하면,     [SignBit, E Field, Mantisa Field] 와 같은 구조로 저장된다고 할 때,
                   E Field 는 E0 + Bias 이다.  (E0 는 원래 지수), 따라서, 저장된 지수필드에서 원래 지수를 구할때는 E0 = Eb - Bias 를 해주면 된다.
                   Mantisa Field 는 1.0 + m1 x 2^-1 + m2 x 2^-2 + m3 x 2^-3 ... 에 대해, m1m2m3... 이 된다.

이 글의 포커스는 실수형 데이터에 대한 비트접근이므로...
나중에 자세히 살펴보도록 하겠다.

비트단위 연산자는 정수형 데이타를 비트로 접근한다.
각 비트의 1은 True, 0은 False.

[비트단위 논리연산자]
~ NOT 비트단위 논리부정 : True 는 False 로, False 는 True 로 ...

예. ~ 0101 0010   =  1010 1101


& AND 비트단위 논리곱 : 둘다 True 일때만 True , 그렇지않으면 False
| OR 비트단위 논리합 : 둘다 False 일때만 False, 그렇지않으면 True
^ XOR 비트단위 배타적논리합(eXclusive OR) : 둘이 다르면 True, 같으면 False

왼쪽으로 원하는 bit 수 반큼민다.
밀려서 잘려나가는 부분은 버린다. 밀려서 생기는 공백은 0 으로 채운다.

>> 오른쪽으로 원하는 bit 수 반큼민다.
밀려서 잘려나가는 부분은 버린다. 밀려서 생기는 공백은 0 또는 1로 채우는데, 이것은 시스템 의존적이다.
unsigned 인 경우에는 << 와 마찬가지로 0 으로 채운다.
반면, signed 인 경우에는 일반적으로 부호비트를 복사해넣는다. 부호비트는 최상위비트로 음수일때 1, 양수일때 0 이다.

<< 와 >> 는 변수값 자체를 변화시키지 않는다.
값을 변화시키려면, <<= 나 >>= 따위를 써서 재배정 해주면 된다.

첨부된 프로그램은 << 와 >> 가 어떻게 작용하는지 보여준다.

첫번째 데이타는 오른쪽으로 밀었을때 모두 잘려나간 데이터가 버려져서, 왼쪽으로 돌아왔을때 사라진 모습을 보여준다.

두번재 데이타는 왼쪽으로 밀려갔다가, 하필 최상위비트가 1이 되는 바람에 오른쪽으로 돌아올때 부호비트로 공백이 채워진 모습을 보여준다.

invalid-file

[필드와 레코드]

데이터가 의미를 갖는 최소단위를 필드라고 하고, 여러 필드가 모여서 하나의 대상에 대한 자료가 된것이 레코드이다.

이러한 관점에서 구조체를 바라보자.

예. struct student { int id ; double score; } ;

위와 같이 스투던트를 나타내는 자료형을 보면, id 를 나타내기위한 4바이트의 영역과, 점수를 나타내기위한 8바이트의 영역을 합쳐, 총 12바이트짜리 데이터타입이 되는 것이다.

이때 첫 4바이트는 id 를 나타내는 필드가 되고, 두번째인 8바이트는 점수를 나타내기 위한 필드이다.
그리고, student 는 4바이트, 8바이트의 두개의 필드를 갖는 레코드라고 할 수 있다.


-----------------------------------------------------------------------------

[비트필드의 구문]

C에서는 구조체나 공용체를 통해서 사용자 정의형을 만들때, 비트 단위로 필드 폭을 셋팅할 수 있는데, 이렇게 비트 단위로 폭이 셋팅된 멤버를 비트필드(bit-field) 라고 부른다. 즉, 그 레코드의 특정 필드를 나타낸다.

비트필드를 선언하는 구문은 다음과 같다.

bit_field_member  ::= { int | unsigned }₁ { identifier }_opt : bit_field_width
bit_field_width  ::= nonnegative_constant_integral_expression

즉, 비트필드는 정수형 멤버만 가능하며, 폭은 음아닌 정수만 가능하다.
폭의 최대값은 워드 길이와 같다. 즉, 32 비트 컴퓨터의 경우 맥시멈 32 까지다.
컴파일러는 비트필드들을 최소의 기계 워드로 packing 한다.

----------------------------------------------------------------------------------------------

[비트필드 타입]

비트필드는 unsigned 비트필드와 int 비트필드 두가지가 있다.

unsigned 비트필드는 당연히 영아닌 음수만 저장이 가능하고, int 형 비트필드는 시스템의존적이다.

다음의 예제를 살펴보자.

예.
struct rcd {
unsigned fd1 : 2 ;           // unsigned 비트 필드, 폭 = 2비트
int fd2 : 3 ;                    // int 비트 필드, 폭 = 3비트
} ;

첫번째 비트필드 fd1 은 2비트이므로, 2의 2승 개, 즉 4개의 정보가 저장이 가능하다.
즉, 0, 1, 2, 3

두번째 비트필드 fd2 는 3비트이므로, 2의 3승 개, 즉 8개의 정보가 저장이 가능하지만, int형 이므로, 저장할 수 있는 형태는 시스템에 의존적이다. 어떤 시스템에서는 폭이 얼마건 간에 최상위 비트를 부호비트로 사용한다.

또한, 시스템마다 비트와 바이트를 워드의 상위부터 카운트 하는지, 하위부터 하운트 하는지가 다르기 때문에 비트필드를 사용한 코드를 다른 시스템에 이식할때는 주의를 요한다.

int 형 비트필드를 테스트 해보기 위해 다음과 같은 간단한 코드를 돌려본다.

예.
#include<stdio.h>
typedef struct { unsigned fd1 : 2 ; int fd2 : 3 ; } rcd;

int main(void){
     rcd a={0};           // 구조체 초기화
     int i;

     for(i=0;i<=16;i++)
          printf("a.fd1= %u \t\t a.fd2= %d\n",a.fd1++ , a.fd2++);

     return 0;
}

위의 루프는 각 멤버를 1씩 증가시키면서 배정하고, 출력한다.

아래는 나의 실행결과이다.

invalid-file