[다변수] 다변수함수의 미분
Math/Calc./Diff. Eq./ Analysis2008. 4. 18. 22:09 |일반적으로, Rn 에서 Rm 으로의 일반 함수에 대해서, 미분은 Rn 에서 Rm 으로의 선형변환이고, 즉, m x n matrix transformation 이 된다.
차근히, 논리를 전개해보면, 이 행렬의 i번째 행은 f의 i번째 component function 의 미분과 같다는 것을 유도할 수 있다.
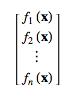
그런데 각각의 component function 은 Rn 에서 R 로의 함수이므로, 컴퍼넌트 펑션의 미분은 1 x n 행렬, 즉 row matrix 가 된다.
결과적으로, Rn 에서 Rm 으로의 함수에 대한 미분은, Rn 에서 R 로의 함수에 대한 미분만 구할수 있으면, 각각의 컴포넌트 펑션들을 미분해서 구할 수 있게된다. 그래서, 그것을 각행으로 하는 메이트릭스를 구하면, 그것이 바로 구하고자 하는 미분이 된다.
Rn 에서 R 로의 함수에 대한 미분은 1 x n 매이트릭스고 j번째 열이 f를 j번째 변수로 편미분한 것이 된다.
참고로, 이것은 그레이디언트 오브 f 의 j번째 성분과 같게된다.
따라서, Rn 에서 Rm으로의 함수에 대한 미분은 m x n 행렬이고, 또한, i번째 행은 i번째 성분함수의 그레이디언트의 성분들을 늘어놓으면 되므로, 결국, i,j 성분은 i번째 성분함수를 j번째 변수로 편미분한 것이 된다.
이를 제이코비언(자코비안,야코비안) 메이트릭스라고 한다.
즉, Rn에서 Rm 으로의 함수 f 에 대한 미분은 f의 자코비안 메이트릭스 이다.
다음번엔 다변수 함수의 테일러 전개에 대해 얘기해보자.
차근히, 논리를 전개해보면, 이 행렬의 i번째 행은 f의 i번째 component function 의 미분과 같다는 것을 유도할 수 있다.
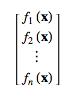
그런데 각각의 component function 은 Rn 에서 R 로의 함수이므로, 컴퍼넌트 펑션의 미분은 1 x n 행렬, 즉 row matrix 가 된다.
결과적으로, Rn 에서 Rm 으로의 함수에 대한 미분은, Rn 에서 R 로의 함수에 대한 미분만 구할수 있으면, 각각의 컴포넌트 펑션들을 미분해서 구할 수 있게된다. 그래서, 그것을 각행으로 하는 메이트릭스를 구하면, 그것이 바로 구하고자 하는 미분이 된다.
Rn 에서 R 로의 함수에 대한 미분은 1 x n 매이트릭스고 j번째 열이 f를 j번째 변수로 편미분한 것이 된다.
참고로, 이것은 그레이디언트 오브 f 의 j번째 성분과 같게된다.
따라서, Rn 에서 Rm으로의 함수에 대한 미분은 m x n 행렬이고, 또한, i번째 행은 i번째 성분함수의 그레이디언트의 성분들을 늘어놓으면 되므로, 결국, i,j 성분은 i번째 성분함수를 j번째 변수로 편미분한 것이 된다.
이를 제이코비언(자코비안,야코비안) 메이트릭스라고 한다.
즉, Rn에서 Rm 으로의 함수 f 에 대한 미분은 f의 자코비안 메이트릭스 이다.
다음번엔 다변수 함수의 테일러 전개에 대해 얘기해보자.
