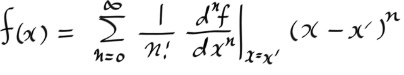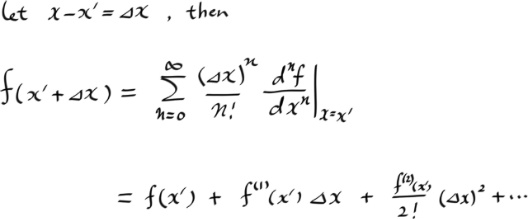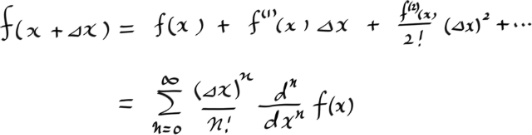The Lienard - Wiechert Potentials are retarded potentials for a point charge in arbitrary motion.
I've skimmed several textbooks; Griffiths (3rd ed.) uses some coarse logic even tho he insists it's Doppler effect, and recommends Reitz's book for the rigorous proof. Reitz uses Jacobian transformation of infinitesimal volume, and 1st-order Taylor approximation for v << c ( not sure about this ) and finaly it's the same as what Griffiths wanted to say. Whereas, Jackson uses relativity.
However, none of them was satisfactory because I wanted to derive the Lienard - Wiechert Potentials in the classical point of view, not relativistic one, so wanted to see if it's true that relativity comes from classical electrodynamics, as professors always emphasize.
So, I wanna do it in a purely classical way to derive the Lienard-Wiechert potentials only from Maxwell's equations, not adding any other facts... theories... whatsoever.
I'll first introduce the retarded potentials for better understanding of non-physics students.
If you already know about the retarded potentials, you can skip the following right after just checking my notation.
the retarded potentials
Maxwell equations tell us EM waves travel at the speed of (permitivity * permeability) -1/2
Then, like i said in the posting about 4D Poisson's equation ( equivalent to Maxwell's equations with the Lorentz gauge ), potentials also propagate at the speed of light.
So, It's quite reasonble or plausible that we sholud estimate potentials at some earlier time cuz obviously it takes some time to reach a point apart. It's like starlight that we see now is actually old one.
Let w(t) be the trajectory of a point charge at time t and we wanna calculate the potentials at a specific point x and time t.
And let v(t) be the velocity of the charge.
Like I said, it takes some amount of time to reach
x , we should deal with the position of q at some earlier time, so it would be good if we know how long we should go back in order to calculate the potential at (
x,t) but unfortunately it not so simple since it depends on the given trajectory
w, aribtray field point
x and time t.
As a result, we should solve the following
implicit equation and it's possible only when the trajectory is given and
x , t are (temporarily) fixed.
The solution of the equation is called
retarded time, let's denote it as
t ret , that is, the above eqaution holds when t' =
t ret .
So, the potentials at (
x, t) must come from the charge density distribution or current density distribution at t' =
t ret .
So here we are.
where primed ones are integration variables. ( just dummies )
This is called
retarded potentials. ( Now we leave the validity of these formulas out of consideration. It's not our topic. )
the Lienard - Wiechert potentials
We're gonna derive Lienard-Wiechert potentials without any redundant conditions but only by elementary integration with delta functions.
First, we know charge density distribution of the point chare is a delta function.
Therefore....
Now we use the property of the delta function.
It's not difficult to show that
Any kind of mathematical physics textbook includes this. A frequently used example is delta[ a(x-b) ] = delta(x-b) / |a| that you're familiar with.
Anyway, we have ...
Therefore...
So the scalar potential is
Let
R(t) =
x -
w(t) and use supscript '
ret ' for the quantities estamated at retarded time with naming retarded position
w ret ,
, retarded velocity
v ret , retarded displacement from the charge to
x as
R ret , then...
and with the same manner , ( just put v(t') into the integral )
These are the Lienard-Wiechert potentials.
So, we are done.
ADD: Sooner or later, I'll post about calculation of potentials of a moving point charge in a constant motion by L-W potentials, and
show that it leads us to the Lorentz Transformation. It's one of the evidences that classical electrodynamics is itself relativistic. and it's gonna be an answer of the quiz :
http://sciphy.tistory.com/942