f(z) 가 도메인 D 상에서 연속일때, 다음은 모두 동치이다.
이런걸 보통 줄여서 TFAE 라고 쓰는데, The Following Are Equivalent . 라는 뜻. 일전에 대수 수업때 선생님께서 , following은 복수취급이고 그래서 are 를 써야된다 라고 말씀하신 적이있는데, 이것은 following 자체가 복수이기 때문이 아니라, 뒤따라 나오는 것들이 복수이므로 지칭하는 바가 복수라서 복수취급되는 것이다. 가령 "다음(한가지 사항일때)은 참이다" 라고 할때는 The following is true. 라고 쓴다.
아무튼...
[TFAE] --------------------------------------------------------------
1) f(z) has an antiderivative in D
2) contour integral of f(z) is path independent in D
3) every contour integral of f(z) for any cloed contour in D is zero.
-----------------------------------------------------------------------
사실 이 정리의 본질은 결국, FTC ( Fundamental Theorem of Calculus ) 와 같다. 간단하게 스케치만 해보자. ( 리얼에서의 FTC 는 이미 알고있다고 가정한다. )
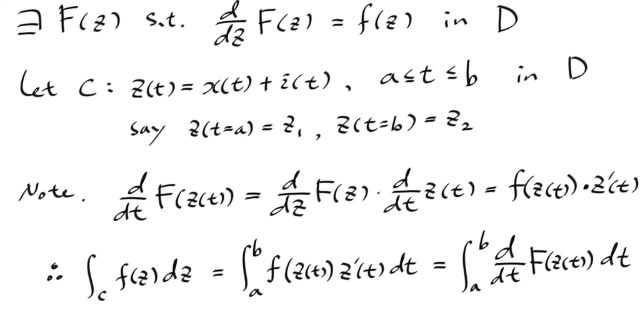
이제 complex-valued 에 대한 FTC 가 되었고, 그것은 본질적으로 실적분과 다를게 없으므로 그대로 성립한다. 따라서...
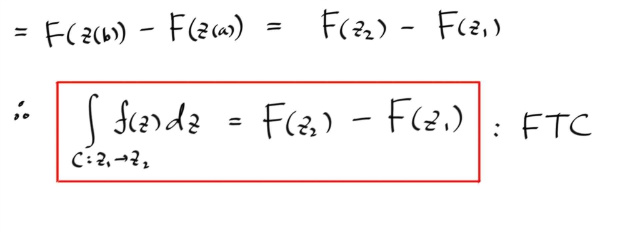
복소수 버전의 FTC 인데, 이것은 실수일때 1차원의 양끝점에만 의존한다에서, 복소평면 2차원에서도 양끝점에만 의존한다는 더 파워풀하게 확장된 FTC 가 되겠다. 개념적으로 따지자면, 실적분의 FTC 가 정적분과 Antiderivatives 를 이어주었던것과 같이, 복소에서는 실적분의 정적분에 대응하는 개념이 컨투어 인테그랄이므로, 복소의 FTC 는 컨투어 인테그랄과 Antiderivatives 를 이어준다고 하겠다.
아무튼, 위의 TFAE 라고 한 정리는 이 FTC 만 알고있다면, 직관적으로 다 와닿는 이야기들이라고 생각한다.
물론, 이 FTC 가 실수일때보다 더 확장된 것은 맞지만, 복소에서는 실수일때보다 antiderivative 를 갖는것이 더 어렵다는 것을 간과해선 안된다.
또한가지 신경써야 할 것은, 칸투어가 포함된 도메인상에서 역도함수를 항상 갖어야 한다는 것인데, 그렇지 않을때는 위에서 TFAE 로 말했던 것들을 하나도 적용할 수 없다.
가령, -i 에서 출발해서 i 로 이르는 두개의 (원점이 중심인) 반원경로를 생각하자. 각각의 경로에 대해, 1/z 를 적분해보면, 한쪽은 π i 가 나오고 또다른 한쪽은 - π i 가 나온다. 즉, 적분값이 경로에 의존한다. 두 경로중에 - π i 가 나온쪽 경로를 반대방향으로 뒤집으면, 폐곡선에 대한 적분이 되고, 이때 적분값은 0 이 아닌 2 π i 가 된다. ( 이것은 [복소함수] #006 contour 적분 1 편 에서의 결과와 같다. )
폐곡선에 대해서 적분했는데도 0 이 안나온것은 폐곡선을 감싸는 어떠한 도메인을 잡더라도, 그안에 싱귤러 포인트인 원점이 들어있기 때문이고, antiderivative 인 log z 도 어떤 브랜치를 잡던지 간에, 그 브랜치 컷에서 log z 가 정의가 안되는데, 도메인 내에 브랜치 컷이 들어있어서, 그부분에서 1/z 을 antiderivative 를 갖지 않게 되기 때문이다.
그래도, FTC 를 이용해서 적분하는 방법이 있는데, 그것은 폐곡선 경로를 둘로 쪼개는 것이다. 그래서 폐곡선 C = C1 + C2 라는 두개의 조각으로 분리하고, C1 과 C2 를 감싸는 도메인 D1 , D2 를 원점 안지나게 잘 잡으면, 각각에 대해, 다른 브랜치컷을 갖어서, 각 브랜치 컷이 각 도메인을 크로스하지 않게 잡은 log z 는 역도함수가 되고, 곧바로 FTC 를 쓸수있게 된다. 이렇게 구한 값도 결국에는 앞에서 구한 결과 2 π i 와 같은 값이 나온다.
----------------------------------------------------------------------------------------------------
이제 우리가 원하는 바는, 앤타이-디리버티브를 이용해서 끝점만 가지고 적분을 하는 것이다 !!
어떤 simple closed contour 를 생각해보자. ( simple closed contour 는 연결상태가 타폴롸지컬리 원과 같은 폐곡선으로, Jordan curve theorem 에 의해, 복소평면을 두 영역으로 나누고, 둘 중 하나는 반드시 bounded 된다. 증명은 터팔로지와 어낼러시스의 지식이 요구되나, 뭐 직관으로 충분하다. 특히, bounded 된 영역이 곧 interior of the contour 가 되고, 그렇지 않은 영역이 exterior of the contour 가 된다. 그리고, 그 컨투어는 당연히 boundary가 된다. 역시 , 직관으로 충분하다. )
아무튼, 어떤 f(z) 가 simple closed contour 에 대해서, 그 내부 (interior ) 와 컨투어 상에서 역도함수를 갖는다면, 이때는 당연히 적분값이 0 이 될 것이다.
그런데, exp ( z ² ) 의 적분을 생각해보자. simple closed contour 에 대해서 적분하려고 하는데, 문제는 저 함수가 antiderivative 를 갖는지 안갖는지를 잘 모르겠다는 말이다. antiderivative 를 알아야 갖는다고 말을 하겠는데, antiderivative 를 잘 모르겠다 이말이다. 그러니 지금으로썬 simple closed contour 에 대한 적분이 0 이라고 말할 수 없다. 앞에서 단순 폐곡선에 대한 적분이 0 이 아닌경우는 숱하게 보지 않았던가.
다행스럽게도, 위와 같은 문제를 해결해줄 아주 간결하면서도 중요한 정리가 있다.
Cauchy - Goursat theorem. ( 코시 - 구르사 정리 , 나는 코시-골삿 정리라고 읽곤했는데, 프랑스 사람이라 어떻게 발음해야 하는지 모르겠다. )

코시는 f ' 이 연속이라는 가정을 하고, 정리를 증명했고, 50 년 뒤에, Goursat 이 그 가정을 제거했다. f' 이 연속이라는 조건을 제거하는 증명과정은 좀 어려우므로 생략한다. 자세한 내용은 관련 교과서를 참조하길 바란다. 참고로, 터팔로지 & 어낼러시스에 대한 내용이 주를 이룬다. 짜증나게 입실론 델타도 자꾸 나오고...암튼, 여기서는
코시의 정리만 증명한다. 즉, f' 이 연속이라고 가정한다.
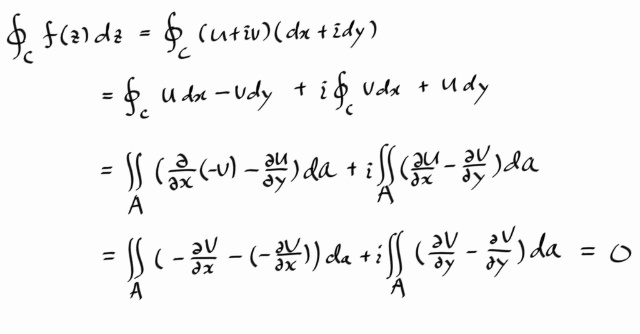
두번째 줄에서 세번째 줄로 넘어가는 것은 Green's theorem 이다. 보통 그린의 정리는 잘 안외워지는 대신, 스토크스 정리하고 가우스 정리는 잘 외워지고 더 많이 쓰이는데, 그린 정리는 사실 그 둘의, 그리고 FTC 의 기하학적 확장에 대한 뿌리이다. 아무튼, Green's theorem 의 공간에서 선과 면에 대한 일반화가 Stokes' theorem 이므로, 그린의 정리가 생각이 안날땐, 스토크스 정리를 평면상의 simple closed path 에 적용하면 된다. 그니까 그냥 두번째 줄에서 세번째 줄로 넘어가는 부분을 스토크스 정리로 넘어와도 된다.
세번째 줄에서 네번째 줄로 넘어오는 것은 코시-리만을 대입한 것이다. 그래서 결과는 0 이 된다. 아 그리고, f' 이 연속이라고 하는것은 그린정리 쓸때 쓰였다. 그린정리를 쓰기위한 조건들로 편미분들이 연속이고 뭐 그런거 있는데, 복소에서 f' 이 연속이면, 결과적으로 f의 편미분들이 모두 연속이고, 그 성분함수들의 편미분들이 모두 연속이므로 그것이 쓰였다. 아 그리고 A 는 C 의 내부이다 -_-
아무튼, 심플 클로우즈드 컨투어에 대해서 적분값이 항상 0 이고, Goursat 에 의해 f' 이 연속일 조건도 제거되어, 간단히, f 가 어낼러틱이기만 하면 ( 물론, 폐곡선 위와 그 내부의 모든점에서 그래야 한다. ) 단순 폐곡선에 대한 적분은 0 이 된다.
따라서, 아까 exp ( z^2 ) 라는 함수는 정확히 역도함수가 뭔줄은 모르더라도, 어디서든 어낼러틱 하므로, 단순 폐곡선 잡아서 컨투어 인테그랄하면 적분값은 항상 0 이 된다.
그럼 이 결론으로 부터, 실적분에 대한 "뭔가" 를 얻을 순 없을까?
일단, 컨투어를 중심이 원점인 단위원으로 잡는다. 물론 반시계방향으루다가... 그리면, z = exp ( i t ) 이고, t 는 0 부터 2 π 까지다. 이제 이 적분이 0 이라는 결론을 알고있으므로, 적분식을 리얼파트와 이매져너리 파트로 쪼개면, 각각 0 이 되어야 할 것이다. 그로부터 뭔가 적분공식을 하나 얻을수 있지 않겠느냐 이말이다.
일단, 해보자.
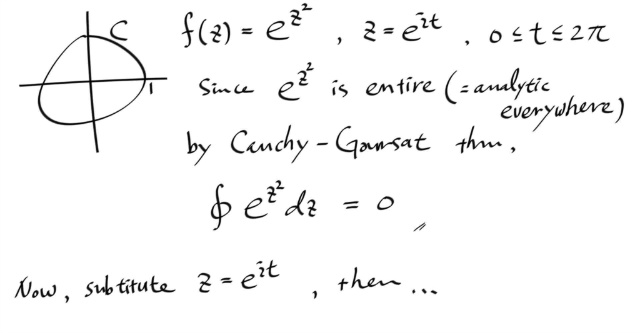
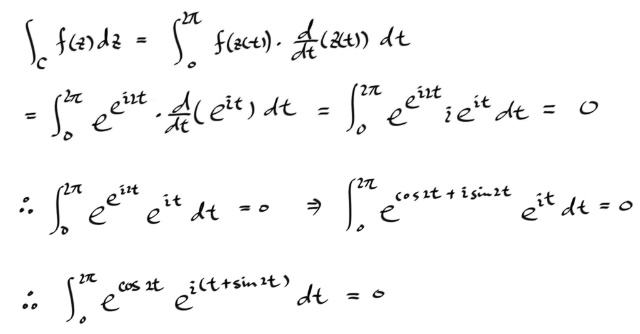
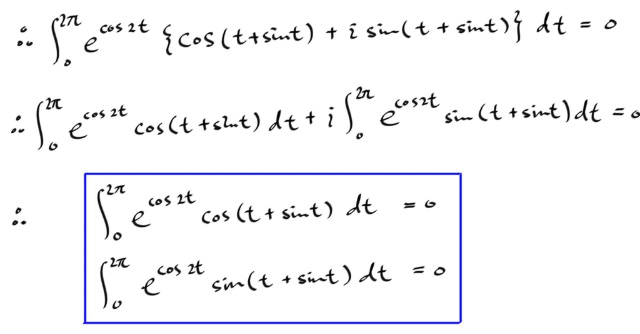
이렇게 얻어진 두개의 적분식은 복소수와는 전혀 무관한 실적분들이다. 우리는 지금껏 복소함수에 관한 이론을 전개해왔는데, 결과적으로 복소수와는 전혀상관없는 실함수 적분 두개를 얻었다.
누구한테든 가서, "당신 저거 적분할수 있어?" 라고 묻자. 그러면 아마도, 부분적분을 줄기차게 반복하거나, 적분표를 찾아보며 끙끙대겠지만, 위와 같은 형태는 왠만한 싸이즈의 적분표에는 안나올꺼라는 말씀. 이때, 속으로, "나는 할수있는데~ㅋㅋ, 답은 0 이라구 ! " 를 외치면 그것이 우리의 성과가 되겠다.
한편, 결과에 대한 의구심이 살짝 드는데, 왜냐면, 우리의 이론전개는 복소수에 대한 이론이었는데, 그것을 덥석 실함수에 관한 이론으로 받아들인다는것이 조금 찝찝한것이다. 왜냐하면, 솔직히 복소수에서야 별 그지같은 소리를 해도, 아 뭐 그렇게 정의하나보다 하고 넘어가면 그만이지만, 위의 두 실함수 적분은 말그대로 피적분함수들 그래프를 그려서 0부터 2π 까지 적분하면 진짜로 0 이 나와야 한다는 검증 툴이 있기 때문이다.
자, 이제 이 의구심을 어떻게 해결할 것인가, 직접 역도함수를 구해서 결과를 확인하던가, 아니면 그래프라도 그려서 어떻게 되는지 눈으로 봐야 의심이 해결될 것 같다. 역도함수를 구하는건 좀 어려워 보이니까, 그냥 그래프를 그려버리자.
좋아. 매쓰매티카로 한줄이면 끈날 일이다. ㅋㅋㅋ.
...
...
...
ㅡ_ㅡ;;; 매쓰매티카를 다시 깔려니 안된다... ㅠㅠ
...
...
...
아... 그렇다. 엑셀로 직접 그래프를 그려서, 모양이라도 보면, 0 부터 2 π 까지 적분했을때 0 이 될지 않될지 대충 감은 잡을 수 있을것 아닌가 'ㅁ' !!! 그..그렇다. 해보자...
일단, exp ( cos2t ) sin ( t + sin2t ) 의 그래프 부터 그려보자... 스텝싸이즈는 0.001 로 하고, 6.28 이 넘어가는 범위까지 계산하자. 수식한줄만 만들면, 나머지는 드래그로 해결되는 엑셀은 정말 사랑스럽다.
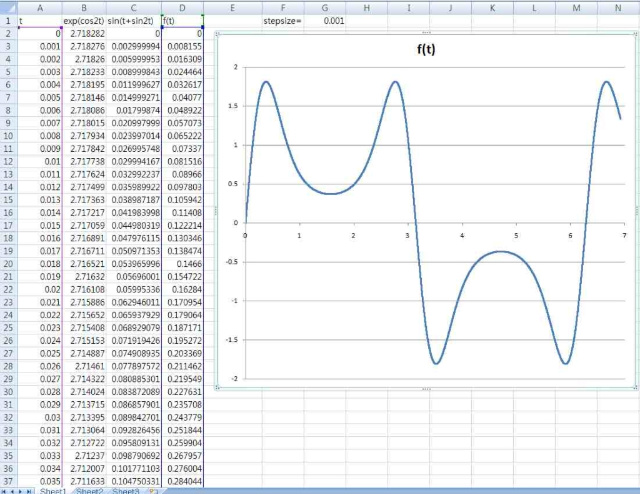
헉!!!!! 그래프를 보는 순간 나는 희열을 느꼈다. 저 지저분한 식에서 저렇게 아름다운 그래프라니, 솔직히 저렇게 예쁜 그래프가 나올거라곤 생각도 못했다. 나는 보자마자, 저 그래프를 0 부터 2π 까지 적분하면 0 이 될꺼라는 확신이 들었다. 아마 누구나가 그렇게 생각할 것이다. 사실 그래프가 개떡같이 나오고 음수쪽과 양수쪽이 좀 애매하게 비슷한 비중으로 나오면, 사다리꼴 방법이나 심슨 메써드 따위를 써서라도 면적을 구해볼 생각이었으나 전혀 그럴 필요가 없게 됐다.
exp(cos2t) cos(t+sin2t) 의 그래프도 그려보자. 수식 하나만 고치면 된다.
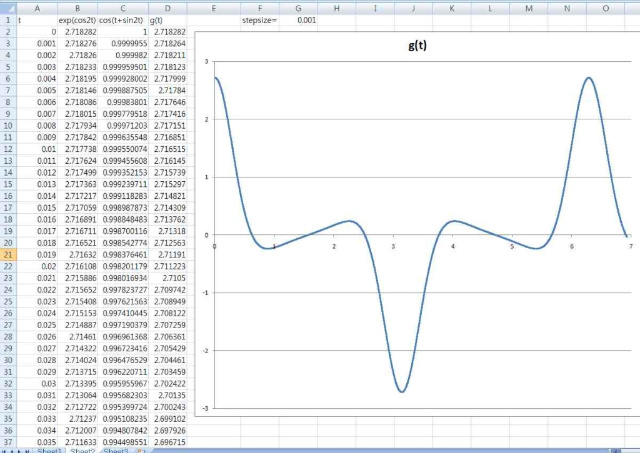
헐... 해보나마나 방금꺼하고 형태가 비슷할거라고 예상했는데, 완전 다르다. 그래도 대칭성으로 부터, 2 π 까지 적분하면 0 이 될것임에는 틀림없다. 특히, 요녀석은 그래프를 볼때, 0부터 π 까지만 적분해도 0 이 나올것으로 보인다. 그러고 보니, exp(cos2t)sin(t+sint) 도 - π/2 부터 π/2 까지 적분해도 0 이 겠구나...
아... 아무튼..... 아.... 아름답다 !!!! '0' !!!!
왠만한 미방이나 각종 문제를 고작(?) 엑셀만 이용해도 얼마든지 분석할 수 있다는 것을 항상 몸소 보여주신 김두철 선생님께 감사드린다.
----------------------------------------------------------------------------------------------------
코시-구르사 정리는 쉽게 다음과 같이 확장시킬수 있다.
" If f is analytic throughout a simply connected domain D , then integral of f(z) on every closed contour lying in D " (증명생략) 주의: D 안에 있는 모든 closed contour 임, simple 아님.
또한, 그로부터, " f that is analytic throughout a simply connected domain D must have an antiderivative in D "
----------------------------------------------------------------------------------------------------
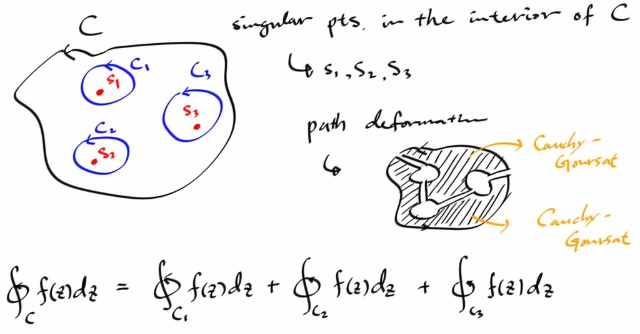
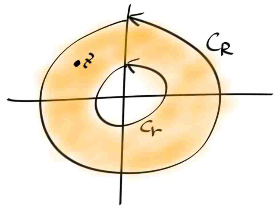
마지막으로 contour 인테그랄을 하는데 있어, 직관적으로 당연한 그러면서 상당히 유용한 테크닉인 Principle of Deformation of Paths 에 대해 살펴보자. 사실 다 면적분할때 배웠던 개념들이다. 아래의 그림만 봐도 뭔내용인지 바로 알수있는 내용이다.
오렌지색으로 표시된 영역이 f 가 어낼러틱한 영역이라고 하자. (경계포함)
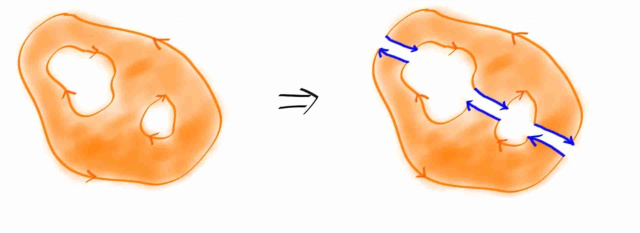
이렇게 쪼개놓고 보면, 왼쪽그림을 따라 적분하나 오른쪽 그림을 따라 적분하나 같다. 오른쪽 그림은 피적분함수가 어낼러틱한 영역을 감싸는 단순폐곡선 두개므로 각각의 적분값은 0 이다. 즉, 왼쪽 그림의 컨투어 인테그랄은 0 이다. 이러한 테크닉은 실제로 매우 빈번하게 쓰인다.
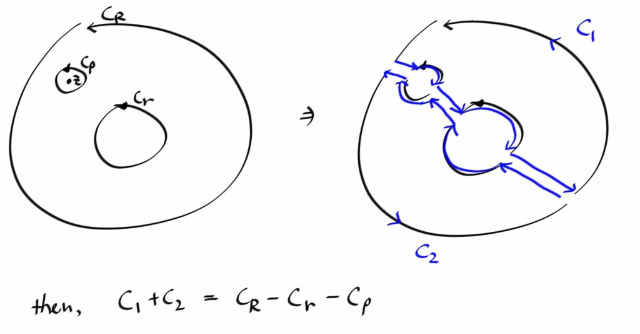
위 성질을 이용하면, 다음의 사실도 쉽게 알 수 있다.
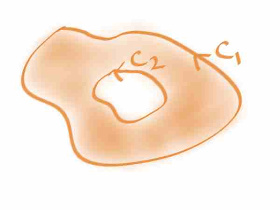
위 그림에서, contour C = C1 - C2 일때 적분이 0 이므로, ( 여기서 - 는 반대방향을 뜻함 ) , 적분의 선형성을 이용해서 적분을 두개로 찢고, -C2 에 대한 적분을 반대쪽으로 이항시키면, C1 에 대한 적분과, C2 에 대한 적분이 같다는 것을 알 수 있다.
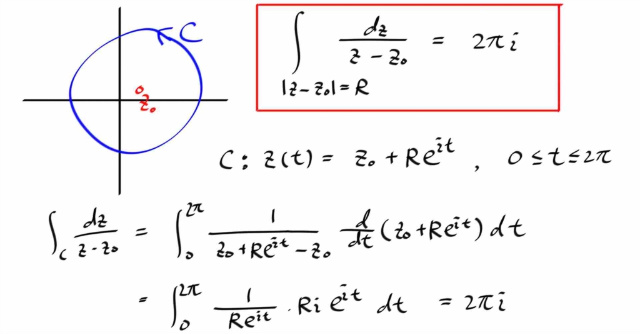
그러므로, 원점을 감싸는 어떠한 단순폐곡선에 대해서도 1/z 을 적분하면 항상 2 π i 이 된다.

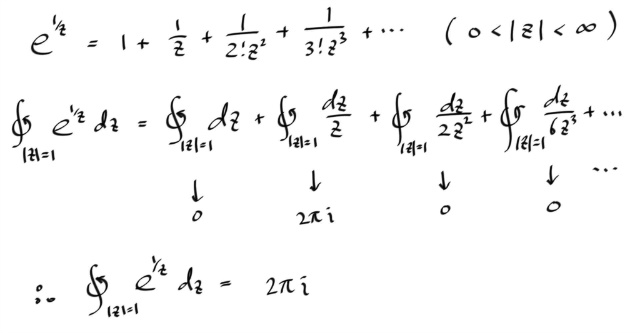



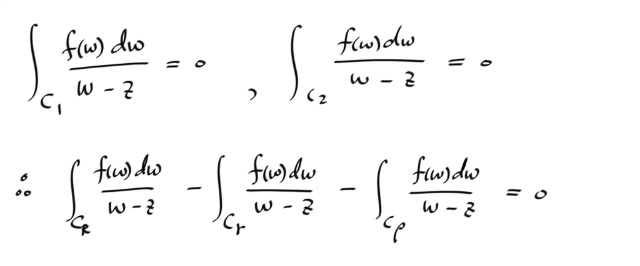
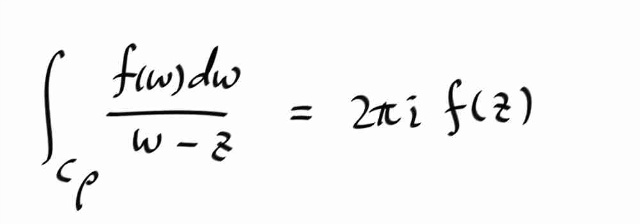
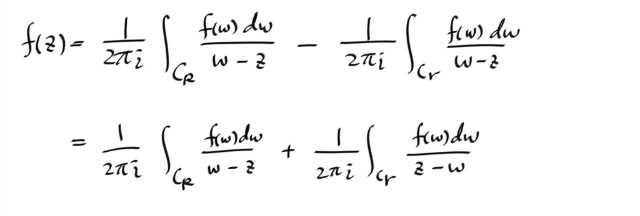
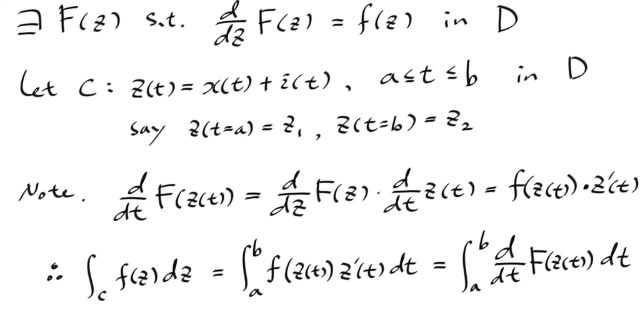
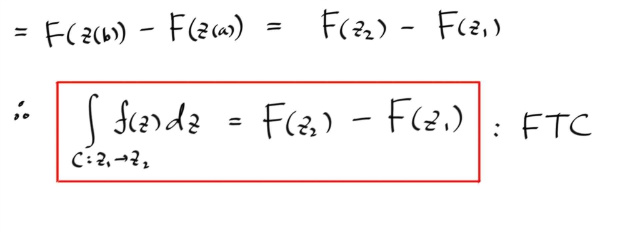

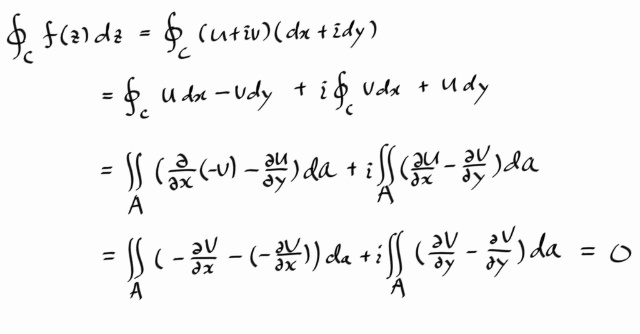
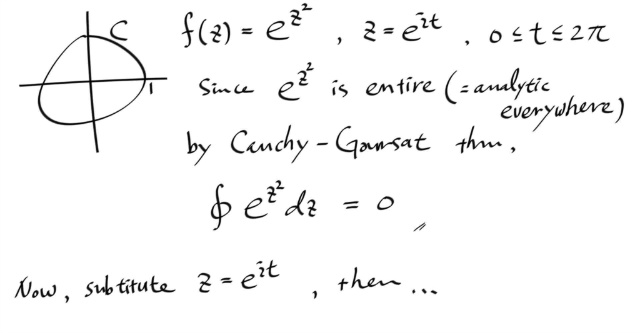
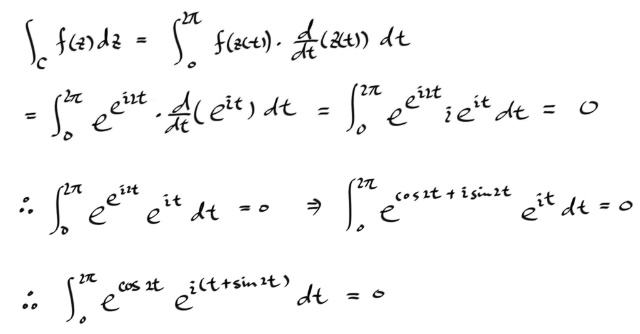
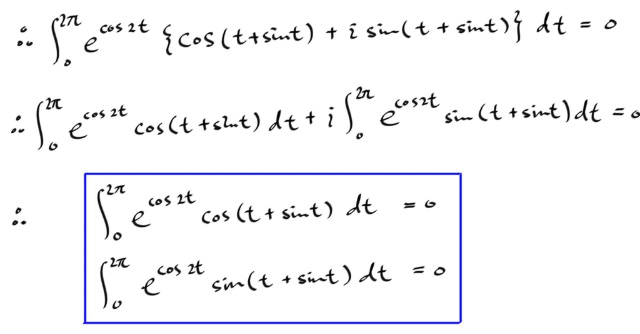




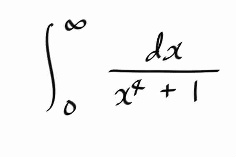
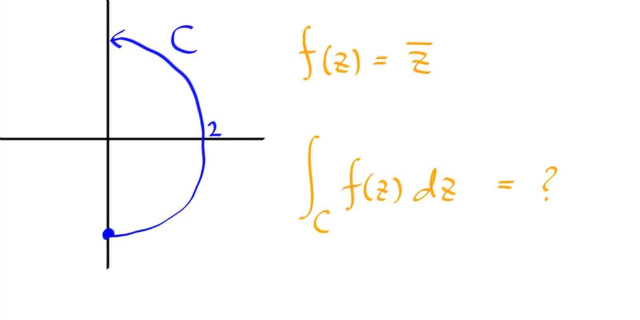

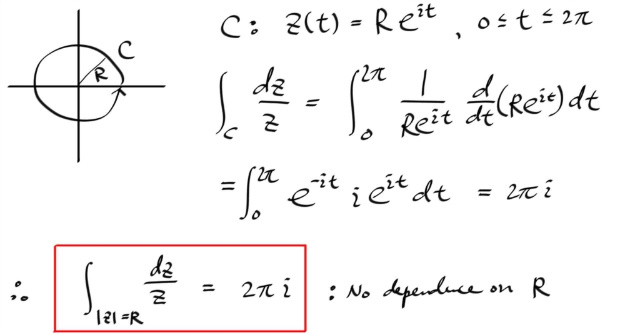
 invalid-file
invalid-file
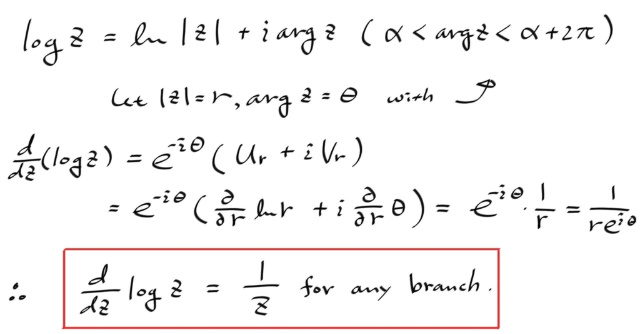
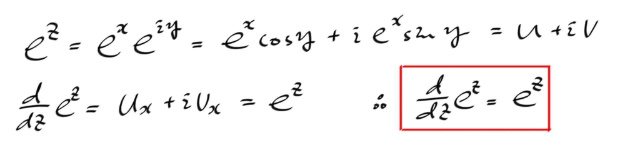









 invalid-file
invalid-file
