[정수론] 전사함수( onto function , surjection ) 의 개수
Quizes2010. 2. 23. 21:40 |집합 X 에서 Y 로의 함수를 생각하자.
전사함수(onto function, surjection) 란, Y 의 모든 원소가 함수의 대응에 사용되는 경우를 말한다.
즉, 공역과 치역이 같은 경우이다.
가령, X = { 1, 2 , 3 } 이고, Y = { 1, 2 } 라고 하면... 다음과 같이 6가지 경우가 가능하다.
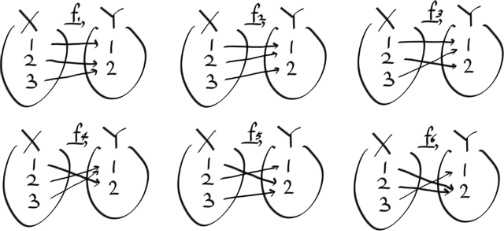
이제, 이것을 일반화 시켜서...
X 의 원소가 m 개이고, Y의 원소가 n 개 ( m ≥ n ) 라고 할 때,
X 에서 Y 로의 전사함수의 개수를 m 과 n 의 식으로 구하여라.
ADD: 결국 개수를 세는 문제이다.
모든 카운팅 문제는, 중복하지 않고 빠뜨림 없이 세는 아이디어만 생각해내면 충분한 경우가 많다.
물론, 그것을 간결한 형태로 나타내는것이 어려울 때도 있지만...
전사함수(onto function, surjection) 란, Y 의 모든 원소가 함수의 대응에 사용되는 경우를 말한다.
즉, 공역과 치역이 같은 경우이다.
가령, X = { 1, 2 , 3 } 이고, Y = { 1, 2 } 라고 하면... 다음과 같이 6가지 경우가 가능하다.

이제, 이것을 일반화 시켜서...
X 의 원소가 m 개이고, Y의 원소가 n 개 ( m ≥ n ) 라고 할 때,
X 에서 Y 로의 전사함수의 개수를 m 과 n 의 식으로 구하여라.
ADD: 결국 개수를 세는 문제이다.
모든 카운팅 문제는, 중복하지 않고 빠뜨림 없이 세는 아이디어만 생각해내면 충분한 경우가 많다.
물론, 그것을 간결한 형태로 나타내는것이 어려울 때도 있지만...
