[C언어] 부동소수점 데이터 타입 ( float, double ) 의 비트 단위 접근 - 첨부파일 : realdata_bit.exe
COM2008. 4. 30. 13:31 |비트단위 연산 & , | , ^ , << , >> 따위는 피연산자가 정수형으로 제한되어있다.
따라서, 단순히 마스크 만들고 & 연산해서 특정위치의 비트를 알아내는 방법은 먹히지 않는다.
문제는 실수형 타입에 비트연산자들이 접근할수 없다는 것이므로, 이것만 해결하면 된다.
간단한 방법은, union(공용체) 를 사용하는 것이다.
공용체에 실수형 멤버와 정수형 멤버를 같이 선언해서, 같은 메모리를 실수형으로도, 정수형으로도 사용할 수 있게 만들면 된다. 그래서, 배정은 실수 멤버에 하고, 비트연산은 정수형 멤버로 하면 간단히 해결된다.
이와같은 방법을 사용하면, 실수데이타의 비트 시퀀스를 볼수있고, 비트처리를 할수도있다.
---------------------------------------------------------------------------------------------------
다음의 첨부파일은 실수형 데이터의 비트단위 출력 프로그램이다. 코드는 위에서 말한것처럼 공용체와 비트필드를 사용하여 작성되었다.
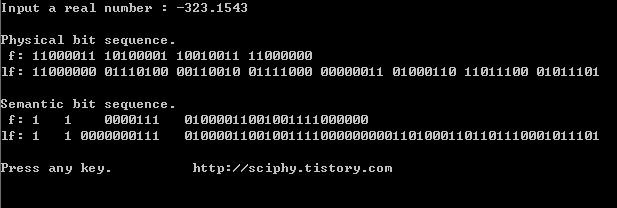
다음은 실행화면이다.
프로그램은 입력된 실수 데이터를 float 형과 double 형으로 비트 시퀀스를 찍는다.
처음엔, 바이트 단위로 묶어서 출력하고,
두번째는, 의미론적 자료구조를 반영해서 찍는다.
실수 데이터의 부동소수점 표현에 관한 표준규약은 IEEE 754 에 포함되어있다.
간단히 언급만 하자면, 부호필드, 지수필드, 가수(mantissa) 필드 이렇게 순서대로 셋으로 쪼개진다.
단, 0.0 은 그냥 모든 bit 값을 0 으로 하는 것으로 정한다.
부호 필드는 float , bouble 둘다 최상위 1비트 이다.
0: non-negative, 1: negative
지수 필드는 float 의 경우 그 다음의 상위 8 비트이며, double의 경우 11비트 이다.
지수 필드의 경우, 크기 비교 등의 이점을 위해, 지수 바이어스 (Exponent Bias) 를 더해서 저장한다.
참고로, single precision bias 는 2^(8-1) -1 = 127 = 0111 1111 이고, double precision bias 는 2^(11-1) - 1 = 1023 = 011 1111 1111 이다.
지수 필드에, 해당 바이어스를 추가해서 더하면, 지수필드의 첫번째 비트(Exp sign bit) 가 오히려 + 가 1 이 된다.
가수필드는 float 의 경우 23비트, double의 경우 53비트 이다. (double 에서 float 로 캐스팅될땐 자료의 손실이 발생할 수 있다.)
가수, 지수, 밑 따위는 모두 2진수 기준이다.
가수필드 저장시 1 + m1 x 1/2 + m2 x 1/4 + ... 식으로 될때, 1 은 생략하고 m1,m2,m3,... 부분만 저장한다. (이진수 이므로, m1, m2, ... 모두 0 또는 1 로, 해당 2^-k 자리 값이 있으면 1 없으면 0 이다.)
가령, float 의 23bit mantissa 필드의 경우, 1.8125 = 1 + 1/2 + 1/4 + 0 + 1/16 => 110 1000 0000 0000 0000 0000 와 같이 된다.
요약하면, [SignBit, E Field, Mantisa Field] 와 같은 구조로 저장된다고 할 때,
E Field 는 E0 + Bias 이다. (E0 는 원래 지수), 따라서, 저장된 지수필드에서 원래 지수를 구할때는 E0 = Eb - Bias 를 해주면 된다.
Mantisa Field 는 1.0 + m1 x 2^-1 + m2 x 2^-2 + m3 x 2^-3 ... 에 대해, m1m2m3... 이 된다.
이 글의 포커스는 실수형 데이터에 대한 비트접근이므로...
나중에 자세히 살펴보도록 하겠다.

 realdata_bit.exe
realdata_bit.exe