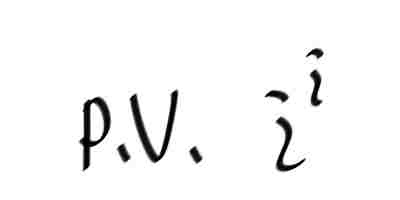[복소변수함수] 복소수 지수 ( Complex Exponents )
Math/Complex2009. 7. 21. 01:06 |수체계의 확장은 방정식과 결부시켜 이해할수 있다. 방정식 x + a = b 의 처리는 음수에 대한 요구를 발생시키고, a x + b = c 의 처리는 유리수로의 확장을 요구한다. 방정식 x² + 1 = 3 따위로 부터, 두수의 비로 나타낼수 없는 수 까지 수의 개념이 확대되었고, 그것의 실존성을 기하학이 제공해주었다는 것이 이채롭다. 이로서 실수체가 완공이 되고, 이전에 존재하던 개념들을 실수체까지 확장하는 것은 대중적으로 꽤 성공을 거둔다.
반면, x² + 3 = 1 따위는 "해가 없다" 정도로 충분했는데, 그것의 "해없음"에 어떤 의미를 부여하려고 해도, 기하학이 무리수 개념을 서포트해주었던 것과 같은 그러한 빽이 없다는 점이 오랜기간 그러한 행위를 한낱 실없는 장난 쯤으로 여기게 만들었다. 아무튼 어찌어찌해서 우리는 복소수 체 까지 오게되었고, 그것은 대수구조(algebraic structure) 체(field) 로서 모든 요건을 갖추었으나, 본질적으로 추상적 대상임은 부인할 수 없다.
자연과학을 하다보면, 복소수 시스템이 얼마나 편리하고 유용한 놈인가를 깨달은 나머지, "세상은 복소수로 이루어져있다" 와 같은 말을 외치고 싶은 기분이 되는데, 사실 그 기분의 정체는 그것의 간결성과 편리성 그리고 효율성이 예상보다 대단한 것이어서 놀라움과 함께 생성된 것일뿐, 복소수 자체의 추상성은 달라질 것이 없다. 어쩌면, 수학 자체는 정의 그 이상도 그 이하도 아니라고 주장하던 어떤 철학자의 말 처럼 우리는 대단한 호들갑을 떨고있는건지도 모른다. 그것에 어떠한 의미를 부여하고 이롭게 사용하는 것은 순전히 인간의 몫이다. 한편, 자연과학자들의 생각은 다를지도 모른다. 특히, 양자물리를 하다보면, 자연을 기술하는 언어는 복소수인가 하는 생각이 드니 말이다.
아무튼, 이제 수 체가 복소수까지 확장되었으니, 밑과 지수도 복소수까지 확장하길 원하는데, 이것의 빌드 과정은 실수때와는 사뭇 다르게 전개된다. 왜냐하면, 실수때처럼 전개하다가는 예상치 못한 모순들이 숱하게 튀어나와 시작부터 순조롭지 못한것이 되므로, 우리는 시작부터 매우 조심스러워야 한다. 그렇지않으면 어느순간 뭔소린지 알수없는 소설을 쓰게 된다.
일단 복소평면상의 모든 점 , 즉, 모든 복소수는 ( 원점은 좀 그렇지만... ) 극형식(polar form)으로 표현이 가능하고 , 여기까지의 논의에는 아무런 문제가 발생하지 않는다. 그러나 지수형식 (exponential form ) 부터는 마음이 복잡해지게 마련이다.
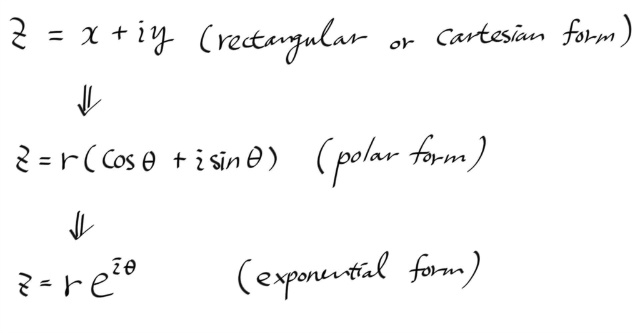
익스포넨셜 폼의 태생적 기원은 오일러 식에 근거를 두는데, 그것은 정리라기보다는 정의임을 강조하는 바이다. 오일러식은 더 기본적인 논의에서 출발해서 복소지수로 차근차근 빌드업이 된게 아니라, 지수함수의 테일러 전개를 복소수 영역까지 확대하는 그 자체를 받아들이는 것으로, 정의를 아주 그럴싸하게(plausible) 만드는 선택이라고 할 수 있다.
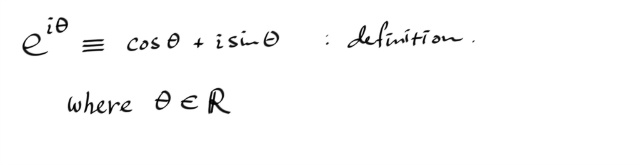
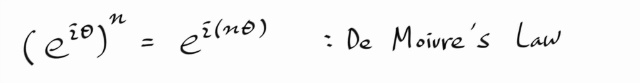
아니 정의에 의해 너무 당연한것 아닌가 하고 물을수도 있지만, 복소수에서 지수법칙이 성립한다는 보장이 없기때문에 결코 당연한것이 아닌것이 된다. 실제로, 복소수에서 지수법칙은 일반적으로 성립하지 않는다. 즉, 위의 정리를 증명하라고 할때 n을 쏙 집어넣고는 증명했다고 하는 것은 현시점에서 넌센스다.
좌변에서 n 이 자연수이므로, 좌변의 괄호안을 정의에 따라 극형식으로 쓰고, 이항전개한후에 그것이 우변을 정의에 따라 극형식으로 쓴것과 같음을 보이면 쉽게 증명된다.
참고로, 오일러 식으로 부터 다음과 같이 쓸수있는데, 많은 사람들은 이것을 수학에서 가장 아름다운 식으로 꼽는다.
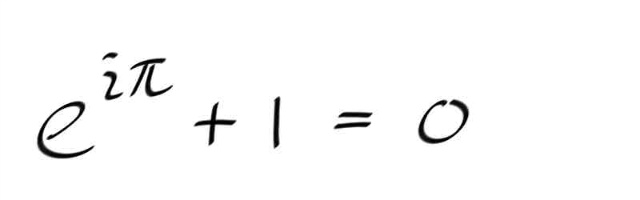
처음에 미적분에서 오일러식을 통해 윗식을 접했을때, 그것은 상당히 감격스러운 것이었는데, 오히려 복소를 배우면서 오일러식을 정의로 채택하면서 그 감격이 상당히 반감되었다는 것은 꽤 슬픈일이다. 마치 나는 대단하다고 생각했던무언가를 누군가가 대수롭지 않게 비웃어 버릴때의 기분?
아무튼, 이제부터 할일은 복소수 지수를 well-behave 하도록 빌드해 나가는 것인데, 당연한 이야기지만, 우리는 이것이 실수체의 그것을 아우르는 더욱 확장된 개념이 되기를 희망한다.
내친김에 오일러식을 이용하여, 밑이 e 인 경우에 대한 복소지수를 정의하자.
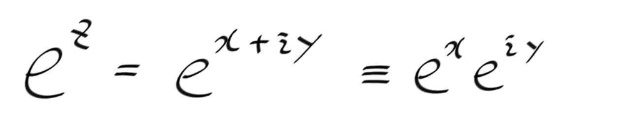
일단 복소수에 대한 정수지수(integral exponents)는 실수에서와 마찬가지로 크게 문제될것이 없다. 자연수는 그만큼 곱하면 되고, 음수가 나오면 역수를 취하면 된다.
유리 지수 (rational exponents ) 부터가 문제이다.
실수였을때 우리는 유리지수를 그것의 밑이 양수일때만 정의했었던것을 상기하자. 그러나 이제 복소수로 온마당에 밑이 양수여야 한다는 제약은 너무나 터무니없는것이다. 실수에서야 음수가 양수와 대비되는 매우 비중있는 녀석인지는 몰라도, 복소수평면에서는 그정도로 비중이 있지는 않달까. 게다가 i 의 태생자체가 밑이 음수인것이지 않은가.
우선 nth root 를 찾는것에서 출발을 하자. ( 늘 그렇듯이 n 은 당근 자연수 )
복소수에서 1/n 승은 " n제곱시 그 수가 되는 수 " 들을 모두 일컫는다는 점에서 실수에서와 차이가 있다. 실수는 1차원적이므로, n-th root 가 기껏해야 +,- 두개밖에 없고, 따라서 + 인것을 정의로 삼고, - 인것은 앞에 - 를 붙여주는 것으로 정의해도 충분하지만, 복소수에서는 한두개도 아니고 또한 2차원적이라 그렇게 쓰는 것은 적절하지 않다. 따라서 1/n 승은 nth root 를 모두 일컫는 대상으로 사용한다.
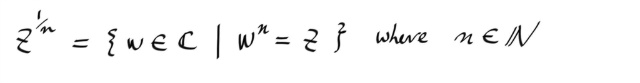
또한 실수에서 했던 것처럼 다음과 같이 쓰자.

주의할것은 위와같이, 실수체계에서 많은경우, x의 1/n 승을, "n 제곱근 x " 로 본다는 것인데, 복소수체계에서는 모든 해를 통칭하므로, "x 의 n 제곱근" 으로 해석해야 된다는 것이다.
즉, 2 의 1/2 승을 , 실수체계에서는 보통 , 루트2 로 쓰고, 대신 나머지 또하나의 근을 그앞에 - 를 붙여서 쓴 반면, 복소수체계에서는 2 의 1/2 승 자체가 +,- 를 둘다 나타내게 된다.
그런데, 실수는 복소수에 포함되므로, 이것은 약간의 혼동을 야기시키는데, 어떠한 복소수의 1/n 승을, 그것의 nth root 를 모두 나타내는 것이라고 해놓고, 그 복소수가 실수가 되는 특별한 상황에서는 + , - 모두를 포함할 것이고, 아예 실수로 고정시켜놓고, 실수때의 시스템을 쓰겠다고 하면 + 일때만을 나타낼수도 있다는 것인데, 이것은 순전히 문맥에 의존하는 경우가 많다.
예를 들어보자.
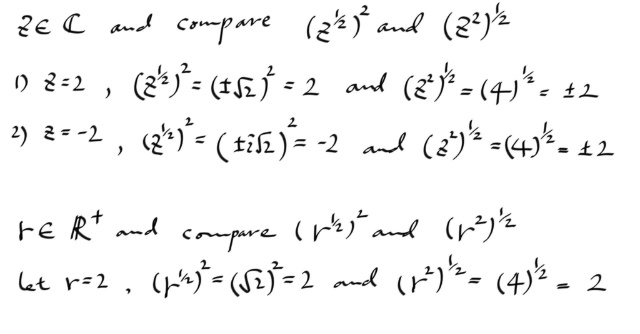
즉, 같은 4에 1/2 승으로 표기햇음에도 불구하고 다른것을 나타내는 것을 볼 수 있다. 따라서, 우리의 컨벤션은 대상의 고려 영역에 따라, 같은 노테이션을 다른것을 나타내는데 사용할 수 있으므로 주의해야 한다.
또한, 실수에서 우리가 쓰던 노테이션은 지수법칙을 만족하고 있지만, 복소수의 경우, 지수법칙이 성립하지 않고있음을 확인할 수 있다.
이제, 1/n 승이 모든 nth root 를 지칭하는 것이라고 할때, 그것을 직접 구하는것은 별로 어렵지 않다. 복소수를 지수형식으로 쓰면, 두 복소수의 상등은 마듈러스는 같고, 편각은 mod 2π 에 대해서 합동임을 이르므로...
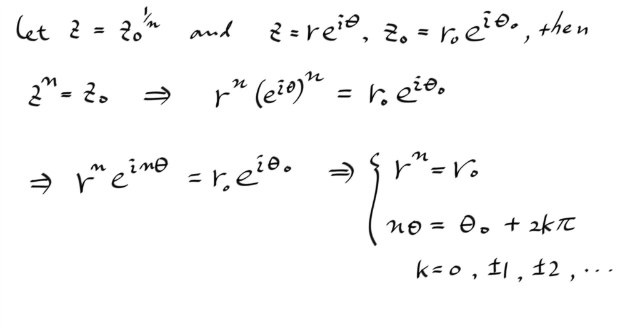
특히, modulus r 은 0 이상이고, 또, 2kπ / n 은 k 가 n 개면 한싸이클이 다 돌게되므로...
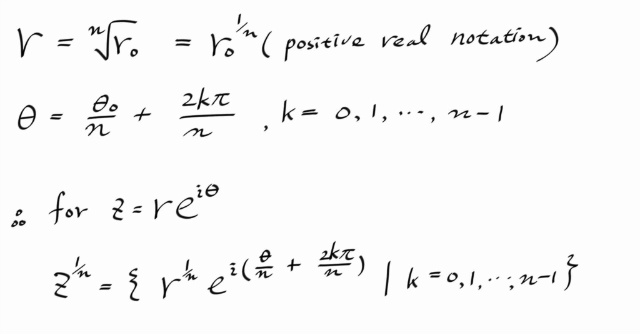
편의상 집합으로 표시했지만, 단지 multi-valued function임을 표현하기 위한 것이다. 또한, r 에 1/n 승으로 쓴것은, r 이 양의실수이므로 그부분에 대해서는 real 에서의 노테이션을 썼다. 복소수일때의 1/n 승과 함께 섞어서 쓴다는 것이 찜찜할수도 있겠지만, 의미상 혼동의 우려가 없으므로 그냥 쓰기로 하자.
아무튼, 위의 결론은 , 복소수의 1/n 승은 디스팅트한 정확히 n개의 대상을 나타내고, 그것은 복소평면상에서 기하학적으로 다음과 같이 컨스트럭트 할수 있다.
" 원점으로 부터 이르는 거리를 1/n 승 하고, 편각을 n 으로 나눈 다음, 그점을 기준으로 원을 n 등분한 점들"이 바로 모든 nth root 들을 나타낸다.
예를 들어 보자.
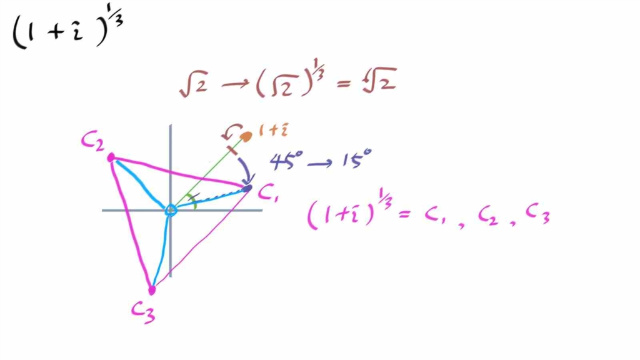
위에서 구한 3개의 수 C1 , C2 , C3 를 3제곱했을때 1 + i 로 돌아가는 방향은 다음과 같다.
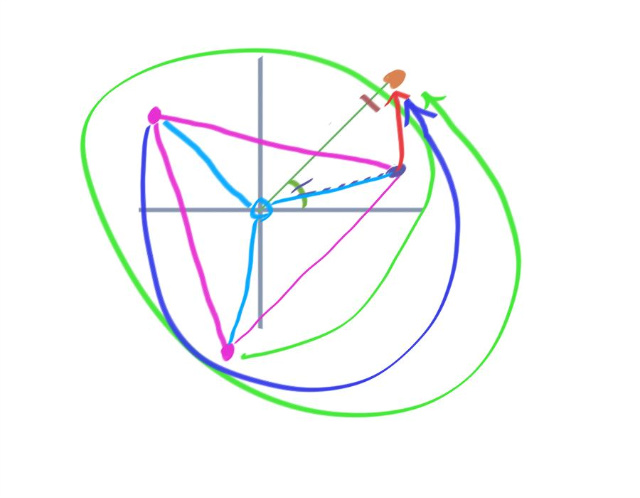
( C3 는 한바퀴 돈다음에 1 + i 로 들어간다. )
또한가지 주의할 것이 있는데, 복소수를 속에다 집어넣은 루트(radical) 기호의 사용이다. 이것도 주의깊게 사용하지 않으면 왠갖 횡설수설은 다 할 수 있다. 고등학교때 이미 많이 겪어봤을것이다. 그러나 이것은 실제로 상당히 신중한 논의를 요하는 것으로 (참고: J. DePree and C. Oehring, Elements of Complex Analysis. Addison-Wesley, 1969), 대충 다루고 넘어갈 녀석이 아니다. 따라서 우리는 이러한 정의를 사용하지 않을 것이다.
이제, 밑이 복소수범위일때, 지수 1/n 을 정의했으므로, m승해서 m/n 꼴만 정의하면 유리지수는 끝나는 거다...? 앞에서 살펴보았듯이, 지수를 적용하는 순서에 의존한다. 따라서 안타깝게도 이것을 안전하게 정의할 방법은 없다. ... /OTL ...
대신, 우리의 정의를 되돌아 보면, 밑이 e 일때, 복소지수에 대해 정의를 해놨으므로, 밑을 e 로 바꿀수 있다면 상당히 편리할 것이다.
그리하여, 결론부터 말하자면, 복소수에서의 로그함수를 도입하고, 그것을 통해, 복소수 밑의 복소수 지수를 실수 밑 e 의 복소수 지수로 바꾸는 방법을 택한다.
복소수에서 로그함수를 정의해보자.
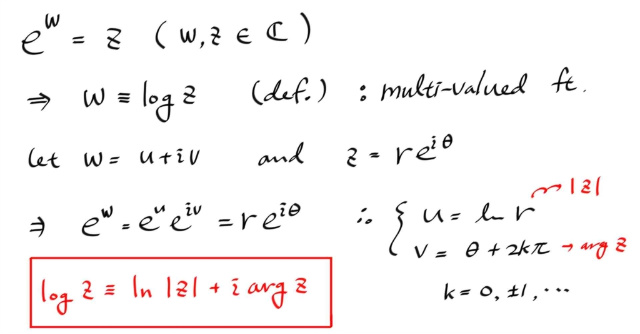
여기서 log 라고 쓴것도 밑이 e 이고, ln 이라고 쓴것도 밑이 e 인데, 굳이 ln 이라고 쓴 이유는 , 실수의 로그함수임을 나타내기 위해서 쓴것이다.
( 이러한 표기는 교과서마다 다른다. )
arg z 가 multi-valued 이므로, log z 도 multi-valued 이다. 특히, 동일한 z 에 대해 arg 값은 2π 단위로 무한히 만들어 내므로, arg 의 범위를 2π 단위로 끊어서 log z 를 싱글밸류드 함수로 만들수 있다. 그 각각을 log z 의 branch 라고 한다. 유사한 예로, 사인함수의 인버스펑션 만들때 구간을 끊어야 했던것을 상기하자.
그런데, 2π 단위로 끊을때, 이게 복소평면상에서 한바퀴가 되고, 그래서 구간의 양끝이 맞닿게 된다.
그 각은 복소평면상에서 원점으로 부터의 반직선이고, 그 반직선을 브랜치 컷 (branch cut ) 이라고 부른다. 주의할것은 브렌치 컷 에서는 로그값이 정의가 안된다는 것이다. 또한 원점에서도 로그가 정의가 안되는데, 그와같은 점을 브랜치 포인트 라고 한다. 브랜치 컷과 브랜치 포인트에 대해서는 이후에 좀더 제대로 포스팅을 하도록 하겠다.
예) the branch of log ( 1 - i ) with π/4 < arg < 9π/4 ( 참고, 1- i 에 대한 로그값을 구할때 branch cut 으로 -π/4 는 안된다. )
log ( 1 - i ) = ln √2 + i 7π/4
브랜치는 임의로 잡을수 있고, 특히, arg z 의 범위가 (-π , π ) 가 되도록 제한한 것을 principal branch 라고 하고 특히 Log z 로 표기한다. 로그함수에 대해서 log ( z1 z2 ) = log z1 + log z2 + i 2kπ 가 된다. 즉, log ( z1 z2 ) = log z1 + log z2 (mod 2π i ) 이다.
이제 복소수의 복소지수를 다음과 같이 정의한다.
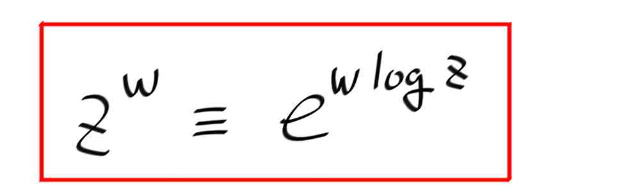
그니까 z 의 w 승을 구할려면, 일단 log z 를 구하고, 그것과 w 를 곱한 결과값(=복소수)를 e 의 지수로 올리면 된다.
특히 z의 w 승을 구할때, principal 로그, Log z 로 하여 구한값을 pricipal value 라고 하고, z의 w승 앞에 p.v. 를 붙여서 쓴다.
이제 이 정의를 이용해서, 복소수의 nth root 를 구해보자. 가령 복소수에서의 2 의 1/2 승은 ±루트2 가 나와야한다.
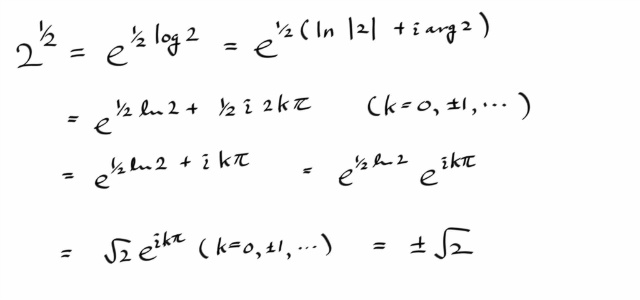
비록 이제 복소지수를 일반적으로 다룰수 있게 되긴 했지만, 우리는 여전히 지수법칙을 사용할 수가 없다.
그나마 특수한 경우에 대해 쓸수있는것을 하나 들어보자면...
n 과 m 이 서로소인 자연수일때, 1/n 을 먼저하든 m 을 먼저하든 결과가 같게된다. 즉, 그 경우에 한해서는 지수법칙중에 지수의 곱 형태로 된걸 사용할수 있다. ( 복소지수에 대한 정의와 정수론적 지식을 이용하면 증명은 어렵지 않다. )
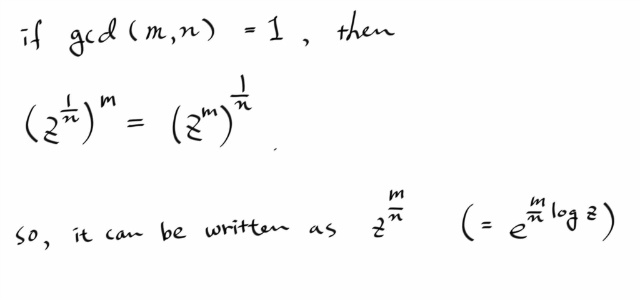
----------------------------------------------------------------------------------------------------
연습문제. 다음을 구해라.