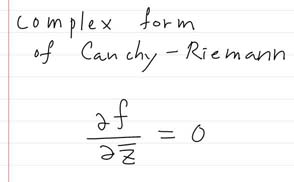코시 - 리만 ( Cauchy - Riemann ) Equations
Math2008. 5. 7. 18:58 |어떤 복소함수 f(z) 를 복소평면상의 어떤 도메인에서 z로 미분한다고 해보자. 복소수 라는게 특이한게, 하나의 수로 표현되었지만 이미 그 안에 두개의 변수를 가지고 있다. 따라서, 어떤점 zo 에서 f를 z로 미분한다는 것은, zo에서 네이버후드를 잡았을때, 그 근방에서 zo에 이르는 모든 경로에 대해 동일한 미분값을 가져야 할 것이다.
따라서, 적어도, zo 에 이르는 수평방향의 편미분이나, 수직방향의 편미분은 같아야 할것이다.
그러므로, f를 z = x + i y 로 미분한다고 할때, y=0 로 놓으면 수평한 경로가 되고, 그때는 dz = dx 가 된다. 또, x=0 로 놓으면 수직한 경로가 되고, dz = i dy 가 된다. 즉, 다음이 성립해야 한다.
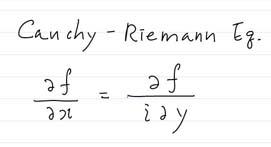
f(z) = u(x,y) + i v(x,y ) 라고 성분함수로 놓고서, 코시리만 이퀘이션을 적용해보자. 그리고, 실수파트와 허수파트를 비교하면 다음과 같이된다.
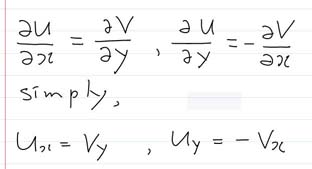
또한, 각 컴퍼넌트 펑션 U(x,y) , V(x,y) 의 x, y 는 z = x + i y 이므로, x 와 y 를 z 와 z bar (complex conjugate 를 bar 로 쓰기로 하자 ) 로 표현할수 있고, 다시말해, x 와 y 가 z 와 z bar 의 함수로 볼수 있고, 각 변수로 편미분을 해보면, 다음과 같은 관계를 얻을수있다.
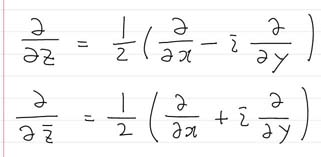
f(z)를 z로 편미분하는건 결국 그냥 z로 미분하는것이 되고, 그렇게 구한것은 Cauchy-Riemann 하고 그냥 같아진다.
또한, 컴플렉스 컨주게이트로 편미분하고 Cauchy-Riemann 사용하면, 결과가 항상 0이 되는데, 이것을 코시-리만 이퀘이션의 컴플렉스 폼이라고 한다. ( 어차피 동치임 )
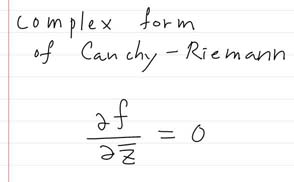
따라서, 적어도, zo 에 이르는 수평방향의 편미분이나, 수직방향의 편미분은 같아야 할것이다.
그러므로, f를 z = x + i y 로 미분한다고 할때, y=0 로 놓으면 수평한 경로가 되고, 그때는 dz = dx 가 된다. 또, x=0 로 놓으면 수직한 경로가 되고, dz = i dy 가 된다. 즉, 다음이 성립해야 한다.
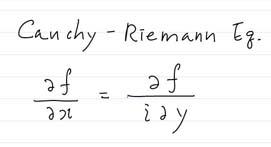
f(z) = u(x,y) + i v(x,y ) 라고 성분함수로 놓고서, 코시리만 이퀘이션을 적용해보자. 그리고, 실수파트와 허수파트를 비교하면 다음과 같이된다.
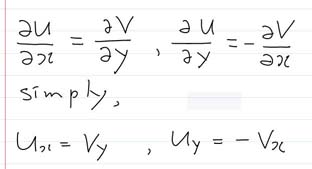
또한, 각 컴퍼넌트 펑션 U(x,y) , V(x,y) 의 x, y 는 z = x + i y 이므로, x 와 y 를 z 와 z bar (complex conjugate 를 bar 로 쓰기로 하자 ) 로 표현할수 있고, 다시말해, x 와 y 가 z 와 z bar 의 함수로 볼수 있고, 각 변수로 편미분을 해보면, 다음과 같은 관계를 얻을수있다.
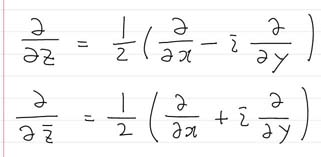
f(z)를 z로 편미분하는건 결국 그냥 z로 미분하는것이 되고, 그렇게 구한것은 Cauchy-Riemann 하고 그냥 같아진다.
또한, 컴플렉스 컨주게이트로 편미분하고 Cauchy-Riemann 사용하면, 결과가 항상 0이 되는데, 이것을 코시-리만 이퀘이션의 컴플렉스 폼이라고 한다. ( 어차피 동치임 )