벡터의 외적 : 수도벡터 ( pseudovector )

우리는 앞에서 벡터의 외적을 물리적으로 정의했었고, 그 정의로 분배법칙이 성립함도 보였다. (외적의 분배법칙 ) 이제 디터미넌트로 된 식을 유도하고, 그것을 Levi-Civita Symbol을 써서 표현한 후에, 그것의 수도벡터리티에 대해 이야기 해보자.


오른손 직교좌표계의 스탠다드 유닛베이시스를 e1, e2, e3 로 잡자.


관찰을 통해,   e1 x e2 = e3 ,  e2 x e3 = e1 ,  e3 x e1 = e2   이와 같은 순환구조로 부터... (물론 순열을 바꾸면 -가 붙는걸 포함해서...)  다음과 같이 Levi-Civita 기호를 써서 나타낼수 있다.

그 다음에 두벡터 A와 B를 그 베이시스로 어낼러틱하게 직교분해해서 쓴 후 분배법칙을 적용하자.

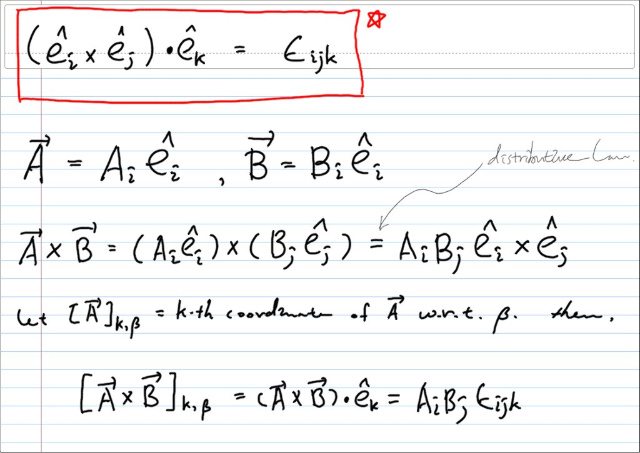
이제 A x B 의 k번째 코오디네이트가 얻어졌으므로, 각 코오디네이트를 베이시스벡터에 프로덕트썸해주면 A x B 를 얻는다.

마지막 식은 디터미넌트와 Levi-Civita 의 관계로 부터 직접 쓸 수있다.  ( 바로 디터미넌트로 쓰는것이 헷갈리면 우선 다음과 같은 행렬 M을 만든다. M_1i = e_i  ,   M_2j = A_j  , M_3k = B_k  그러면 ε_ijk 과 함께 곧바로 | M |  이 된다. )
 


비록 cross product 를 vector product 라고 부르는 것이 아주 일반적이지만, 그러면서도 엄밀하게 구분하자면, 두 벡터의 외적은 수도벡터이다.

만약, 벡터의 외적이 진짜의(?) 벡터라면, 그것은 직교베이시스변환에 대한 성분변환식을 만족해야 할 것이다.

즉, 임의의 두 직교좌표계에 대해, 어느 한쪽에서 연산한 i번째 성분과 다른 한쪽에서 연산한 i번째 성분사이에는 우리가 일전에 λ로 불렀던 좌표변환 공식이 성립해야 할 것이다.


이것을 구분해서 표기하기 위한 노테이션을 도입하자.

오퍼레이터에다가 연산이 어디에서 수행되는가 를 표현해주고, 벡터의 코오디네이트는 어느베이시스에 대한것인가를 나타내주는 것이다. 가령, 연산자에는 프라임이 없는데, β' 대한 코오디네이트라면, 그것은 β 에서 연산한 후에 β' 으로 변환한 좌표가 된다.

그래서, 결국 우리가 하고싶은 말은 " 같은 베이시스에 대해서는 같은 코오디네이트를 가져야 할 것 아닌가! " 이다.


이제, 계산을 해보자.

보통의 경우 ( 적합한(proper) 직교회전의 경우 ) 에는, 아무런 문제가 없으나, 위에서 보듯이, 같은 베이시스에 대한 코오디네이트임에도 불구하고 임프라퍼 로테이션에 대해서는 같지가 않다.

즉, 이것은 어디서 연산했는가에 영향을 받고 있는 것이다. 우변의 앞에 디터미넌트 람다로 부터, 벡터의 외적은 수도벡터임을 알 수 있다. 즉, 임프라퍼 로테이션에 대해 그것은 우리가 아는것과 반대방향의 벡터를 줄 것이다. 참고로 외적의 수도벡터리티는 Levi-Civita 의 수도텐서리티와 같다. Levi-Civita 를 좌표변환해보면 곧바로 디터미넌트 람다라는 팩터가 튀어나온다.


어떠한 물리법칙이 외적을 직접적으로 포함한다면, 관찰 혹은 계산에 있어, 엉뚱한 결과를 줄 수 있음을 말해준다.

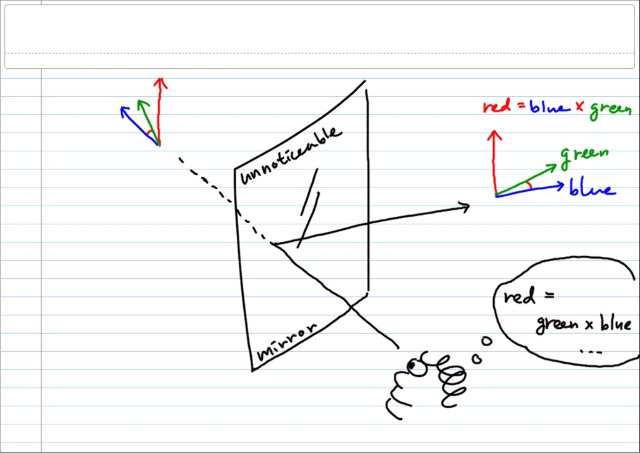
이러한 수도벡터리티는 벡터가 회전성을 포함할 경우에 나타난다. 인버전에 의해 회전성이 뒤바뀌기 때문이다. 즉, 회전방향을 포함한 회전축 벡터가 수도벡터이다. 그런뜻에서 수도벡터를 axial vector 라고도 부른다.  가령 각속도 벡터라든가, 토크라던가, 각운동량이라던가... 이러한 벡터들은 모두 수도벡터이다.

한가지 재밌는 특징은, 회전적 특성이 두번중복되면 상쇄된다는 점이다. 가령, 엑시알 벡터인 각운동량 벡터에 벡터를 외적하면 회전성이 상쇄되어 보통의 벡터가 된다. 마찬가지로, 세벡터 A,B,C 에 대해, A x B 는 수도벡터이지만, A x ( B x C ) 는 벡터가 된다.