외적 (cross product) 의 분배법칙

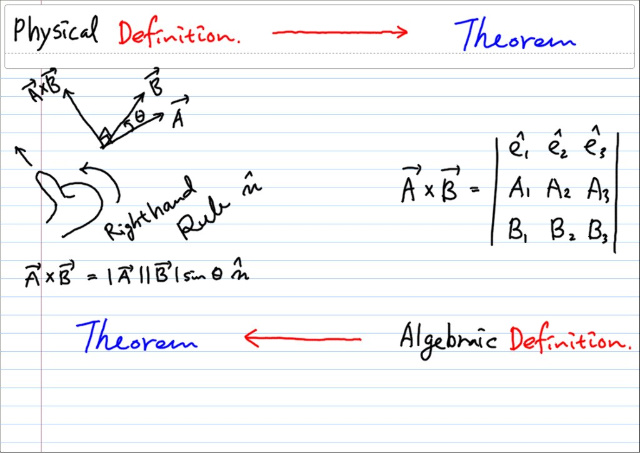
벡터의 외적은 아래 그림과 같이 오른손 법칙을 이용해 정의한다. 물리에서의 벡터(vector)라 함은 단지 벡터스페이스의 element 가 아닌 physical entity 라 했으므로, 이렇게 정의하는것은 매우 물리스럽다(?)고 하겠다. 한편 다소 수학적으로 어낼러틱하게 외적을 다루고자 할 때는, 디터미넌트를 이용해서 정의를 할 수가 있다. 디터미넌트와 Levi-Civita symbol 의 관계로 부터, 그것은 Levi-Civita 에 의한 외적의 정의와 같은것이라는 걸 알 수 있다.


어느쪽을 정의로 삼아도 좋지만, 두가지를 동시에 정의라고 할 수는 없다. 어느 한 쪽을 정의로 삼았으면, 다른 한쪽은 그것으로 부터 유도되어야 한다. 오른손법칙으로 정의하는것이 아무래도 물리적의미를 더 잘 보여주므로 우리는 그것을 정의로 삼도록 하겠다. 이제 디터미넌트로 표현된 식은 정의가 아닌 정리인 것이다.


따라서, 아직 증명하지도 않은 정리로, 외적의 분배법칙 [ A x ( B + C ) = A x B + A x C ] 을 보이는 것은 넌센스다.

참고로, 오른손 법칙에 의한 정의에서, 만약 분배법칙을 증명하면... 디터미넌트 표현식은 쉽게 유도가 된다.


이는, 궁극적으로 "디터미넌트 표현식이 오른손법칙을 만족하는가?" 의 문제가 결국엔 "물리적 정의로 분배법칙이 성립하는가? " 와 같은 문제가 됨을 말해준다.



주의할 것은, 외적의 분배법칙이 마치 당연한 것처럼 얼렁뚱땅 넘어가는 책들도 있다는 것이다. 어떤책은 세벡터를 한평면에 놓고는 증명했다고 사기를 치기도 한다. 실제로 non-coplanar 인 세 벡터를 그려서 증명을 시도해보면, 그것이 그렇게 만만한 녀석은 아님을 깨닫게 된다. 안해봤다면 꼭 한번쯤은 직접 그려서 시도해보길 권장한다.




이제, 증명을 해보자. ( 다음은 토마스 캘큘러스에 나오는 방법이다. )


우선 다음의 보조정리를 보이자.


Lemma.  ----------------------------------------------------------------------------------------------------

A X B 는, B를 A에 수직인 평면에 프로젝션 한 뒤,
A를 축으로 오른손 90도 회전하고 A의 크기를 곱한 것과 같다.

-------------------------------------------------------------------------------------------------------------

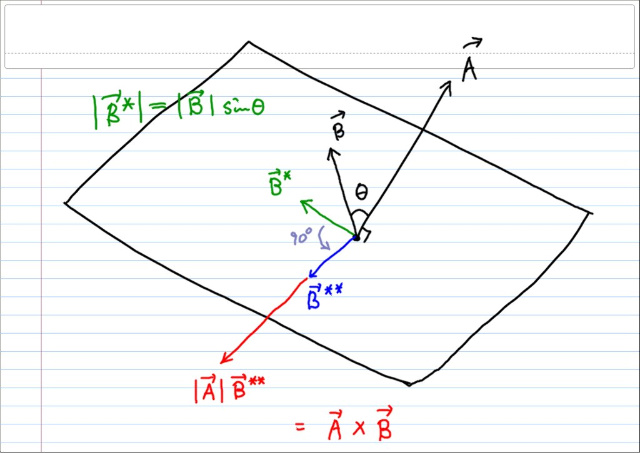
그림에서, B* 는 B를 A에 수직인 평면에 프로젝션시킨 벡터이고, 그 크기는 B sin θ 가 된다.   B** 는 B* 를 A를 축으로 90도 오른나사방향으로 회전시킨 벡터이다. 이 벡터는 크기는 B sin θ 이고 방향은 A x B 와 같다. 그러므로 이벡터에 A의 크기를 곱해주면 A x B 가 된다.


이제 위 lemma 를 이용해, non-coplanar 인 세벡터 A, B, C 에 대해서, A x ( B + C ) 를 구해보자. 여기서도 *는 A에 수직인 면에 프로젝션 한 것이고, ** 는 그것을 90도 회전시킨 것의 의미로 쓰겠다.


그러면 A x ( B + C ) = |A| ( B + C )**  가 될 것이고,   A x B 는 |A| B** ,    A x C  는   |A| C**  가 될 것이다.
이제 우리가 보여야 할 것은 |A| ( B + C )**  =  |A| B**   +   |A| C**    이 된다.

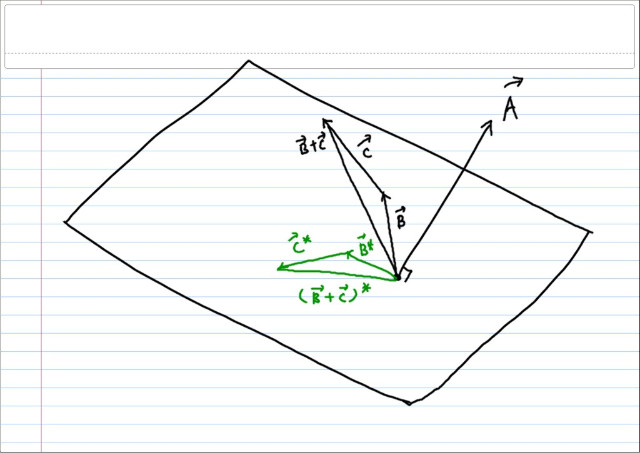
그림에서 보듯이, B , C , ( B+C ) 가 이루는 삼각형의 타폴로지컬 관계는 프로젝션 후에도 보존된다. 이것이 증명의 핵심이다.


이제 삼각형 그대로, A를 축으로 90도를 돌리고 A의 크기로 스케일링 하면 증명은 끝난다.

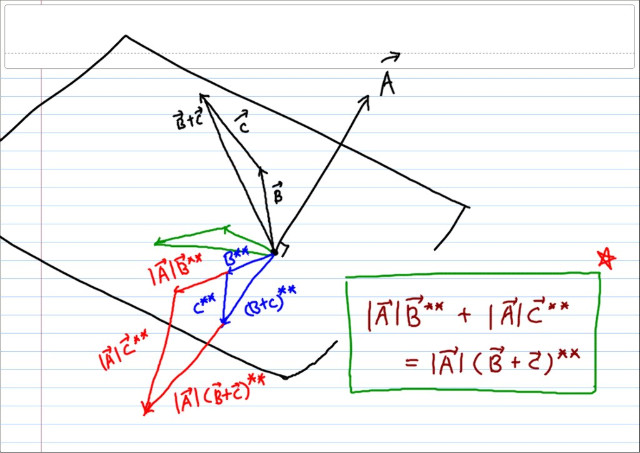
따라서 A x ( B + C ) = A x B + A x C  이 성립한다.