스칼라 삼중적 , 벡터 삼중적, 벡터 사중적
Physics/Math./Mech./Gen. Relativity2009. 1. 14. 20:44 |내적과 외적을 조합해서 쓰는 연산중에 자주쓰이는 기본적인 연산 몇개만 살펴보자.
1. A · ( B x C ) 스케일러 트리플 프로덕트 라고 불린다. 실제로는 스케일러가 아니고, 수도스케일러 이다. 외적이 하나 들어있어서 그렇다. 즉, 인버전이 있는 좌표변환에 대해 반대부호의 값을 준다. 굳이 어낼리틱하게 수식으로 쓰진 않겠다. 참고로, 이값의 절대값은 세 벡터가 만드는 평행육면체 ( parallelopiped ) 의 부피를 나타낸다.
2. A x ( B x C ) 벡터 트리플 프로덕트 라고 불리고, 외적이 두번 중복되어서 곱해지므로, 벡터이다. 즉 수도 벡터리티가 상쇄된다. 어낼러틱하게 전개를 하면 다음과 같이 되고, 흔히 "백-캡" 룰 로 불린다.
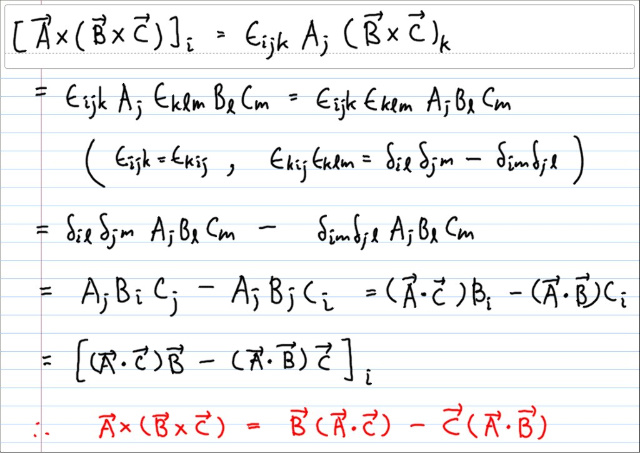
위에서 Levi-Civita 두개가 중복첨자 한개를 가졌을때 Kronecker 로 바꾸는 공식을 이용했다. ( 참조 : Levi-Civita 와 Kronecker )
벡터인지 확인하고 싶으면, 직교베이시스회전 해보면 금방 알 수 있다.
3. ( A x B ) · ( C x D ) 이걸 벡터 사중적 ( vector quadruple product) 라고 부르는건 좀 우끼는듯. 왜그랬을까... 일단 결과는 스케일러이다. 역시 어낼러틱하게 전개를 해보자.

여기서도 마찬가지로 Levi-Civita 를 Kronecker 로 바꾸는 공식을 썼다. 최종적으로 위와같이 간단한 형식으로 쓸 수 있다. 역시 외적 두번곱해지면서 회전성이 상쇄되고, 스케일러가 된다.
4. ( A x B ) x ( C x D ) 이것도 벡터 사중적이라고 부르기도 하는데... 결합법칙 성립 안하므로, 괄호를 다르게 묶는 몇가지 다른 경우도 있을 수 있고...그냥 좀 그렇다. 암튼, 위와같은 방식으로 하면 어렵지 않게 전개할 수 있다.
1. A · ( B x C ) 스케일러 트리플 프로덕트 라고 불린다. 실제로는 스케일러가 아니고, 수도스케일러 이다. 외적이 하나 들어있어서 그렇다. 즉, 인버전이 있는 좌표변환에 대해 반대부호의 값을 준다. 굳이 어낼리틱하게 수식으로 쓰진 않겠다. 참고로, 이값의 절대값은 세 벡터가 만드는 평행육면체 ( parallelopiped ) 의 부피를 나타낸다.
2. A x ( B x C ) 벡터 트리플 프로덕트 라고 불리고, 외적이 두번 중복되어서 곱해지므로, 벡터이다. 즉 수도 벡터리티가 상쇄된다. 어낼러틱하게 전개를 하면 다음과 같이 되고, 흔히 "백-캡" 룰 로 불린다.
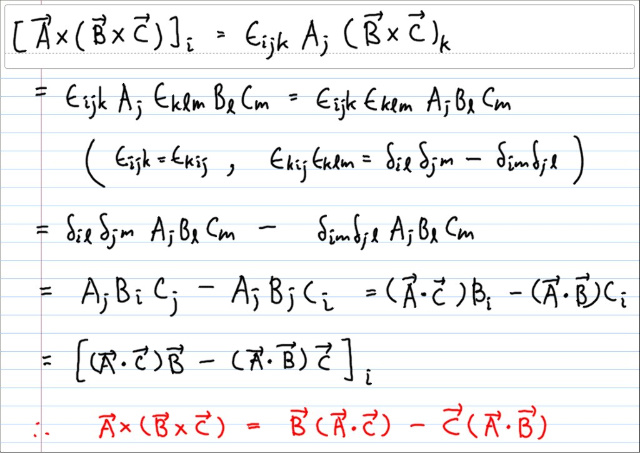
위에서 Levi-Civita 두개가 중복첨자 한개를 가졌을때 Kronecker 로 바꾸는 공식을 이용했다. ( 참조 : Levi-Civita 와 Kronecker )
벡터인지 확인하고 싶으면, 직교베이시스회전 해보면 금방 알 수 있다.
3. ( A x B ) · ( C x D ) 이걸 벡터 사중적 ( vector quadruple product) 라고 부르는건 좀 우끼는듯. 왜그랬을까... 일단 결과는 스케일러이다. 역시 어낼러틱하게 전개를 해보자.

여기서도 마찬가지로 Levi-Civita 를 Kronecker 로 바꾸는 공식을 썼다. 최종적으로 위와같이 간단한 형식으로 쓸 수 있다. 역시 외적 두번곱해지면서 회전성이 상쇄되고, 스케일러가 된다.
4. ( A x B ) x ( C x D ) 이것도 벡터 사중적이라고 부르기도 하는데... 결합법칙 성립 안하므로, 괄호를 다르게 묶는 몇가지 다른 경우도 있을 수 있고...그냥 좀 그렇다. 암튼, 위와같은 방식으로 하면 어렵지 않게 전개할 수 있다.
