[미적, 역학] 반구각의 질량중심

질량중심은 질량비에 의한 내분점이고 x, y, z 축에 대해서 다 생각할수 있으므로 벡터로 나타내면 편하다.

질량중심을 Center of Mass 라고 하고, 질량분포가 균질(homogeneous)하여 결과적으로 질량텀을 제거할수 있어서 단순히 기하학적으로만 질량중심의 위치를 나타낼때를 Centeroid 라고 한다.

 r_cm = < x_cm , y_cm , z_cm > 에서 x_cm = (1/M) ∑ m_i x_i  요렇게 되고. y , z도 마찬가지, 벡터형식으로  묶어쓰면..

             discrete : r_cm = (1/M) ∑ m_i r_i   , continuous : r_cm = (1/M) ∫  r dm

위 식에서 x_cm 식을 보면, y 의 좌표 , z 의 좌표는 들어있지 않다.

즉, 질량중심의 x 좌표를 구하는데 y,z 좌표는 영향을 미치지 않는다. 

1. 원뿔

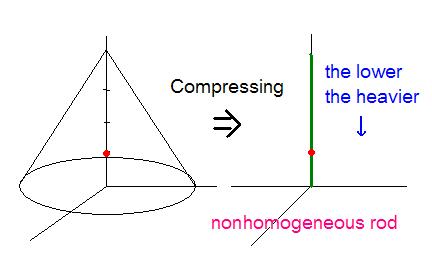
원뿔은 질량중심은 꼭지에서 밑면 원의 중심을 잇는 선분을 3:1 로 내분하는 점에 있다.

이때 꼭지점을 수평이동하여 오블리크 원뿔을 만들더라도 질량중심의 높이는 변하지 않는다.

원뿔을 압축해서 바늘처럼 된다면 질량중심의 위치는 어떻게 되는가 하는 질문은

압축하는 동안 원뿔의 높이성분은 변하지 않았으므로 그 성분에 대한 질량중심의 좌표는 변하지 않는다.

모양이 막대처럼 바뀌었다고 하더라도 질량밀도가 nonhomogeneous 이기 때문이다.

실제로 질량밀도가 변하는 막대(rod) 의 질량 중심을 구할때, 역으로 질량밀도가 균일한 입체로 바꿔서 푸는 방법도 있다.

2. 반구각

반구각의 질량중심도 높이만 구하면 된다. 적분으로 풀면 설정하기에 따라 다양하게 풀수가 있다.

일단, 적분으로 풀고, 다시 간단한 방법으로 풀어보자.

반구각을 x² + y² + z² = R² 이라고 하고, 질량중심의 높이는  z_cm = (1/M) ∫ z dm 이다.

반구각면을 S라고 하면, 면 질량밀도를 σ = M / S = M / (2 π R ² ) 이라고 놓는다.

z_cm = (1/M) ∫ z dm = ( σ / M ) ∫ z dS 가 됩니다. 여기서 dS 는 표면의 면적소이다. 인테그랄은 2중적이다.

높이에 따른 고리를 dm 으로 잡는 방법, 구좌표로 dS와 z를 표현하는 방법 등이 더 쉽다 ;;

구각을 xy plane 으로 정사영 하면 x² + y² = R² 이 되고, 넓이 π R ² 인 이 영역을 A 라 하자. 그리고 적분영역을 S에서 A로 바꾸면 면적소 dA= dx dy 이고, 수직위로 대응되는 dS cos θ = dA 가 된다.

즉, dS = dA / cos θ 이므로 적분영역을 A로 바꾸면 z_cm = ( σ / M ) ∫ z (dA /cosθ) 가 된다.

두 면이 이루는 각은 두 면의 노말벡터가 이루는 각과 같다.

dA 의 normal 벡터는 z축의 단위벡터로 잡고,  k 라고 하자.

dS의 노말벡터는 n = < x , y , z > 이다. 중심으로 부터 구면쪽으로 나오는 벡터다.

참고로 임의의 음함수꼴 곡면에 대해서는 그 음함수의 그레이디언트를 normal 벡터로 삼으면 된다.

(함수값이 가장빠르게 증가하는 방향은 곡면에 수직이기 때문이다. 그러면 타원껍데기도 구할수 있다.)

아무튼  n · k = <x,y,z> · <0,0,1> = z = |n||k| cos θ = R cos θ , 그러므로 cos θ = z / R 가 된다.

∴ z_cm = ( σ / M ) ∫ z (dA /cosθ) = ( σ / M ) ∫ z (R/z) dA =  ( σ / M )R ∫ dA 이 된다.

 적분영역이 어차피 A로 바꼈으니 ∫ dA = A =  π R ² 이 된다. (밑으로 사영된 영역의 넓이A)

∴ z_cm =  R  π R ²  σ / M = R /2 가 된다. 즉 반구각의 질량중심의 높이는 R / 2 이다.

다른 방법으로 풀어보자.

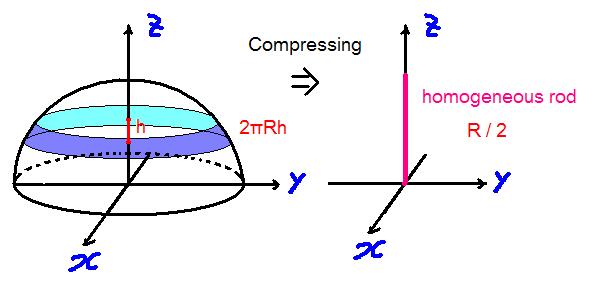
원을 회전시켜 구각을 얻을때 회전축의 미소길이 h에 대해 미소회전면의 넓이는 2πRh 가 된다.

이것은 고등학교때 회전체 파트에도 나온다. 아무튼 , 이것은 구의 아주 특이한 성질이기도 한데, 겉둘레면의 넓이가 중심축의 길이에만 의존한다는 거다.

혹자는 이걸 보고, 구형의 빵을 동일한 폭으로 썰면, 같은 양의 크러스트(빵껍질)를 얻을수 있다 고 말하기도...

또 어떤사람은 수박을 일정간격으로 썰면, 꼬다리쪽이나 가운데쪽이나 껍질의 면적은 같다 라고...  ㅡㅡㅋㅋ  아무튼 이러한 성질을 이용해서, 구각을 덮어놓았을때 높이축에 대해 미소길이를 잡으면 미소겉둘레넓이는 같게되고 , 따라서 구각에 대해 균일한표면질량분포를 가정했으므로, 미소축길이에 대한 미소테두리넓이는 같은 질량을 같게 된다.

이제 이 구각을 아까 원뿔과 같은 방식으로 압축하면 균질한 질량밀도를 갖는 막대가 된다.
그러므로 R/2 가 된다.

적분 결과와 일치한다!