[양자역학] 슈뢰딩거 픽쳐 ( 해밀토니안 연산자가 시간에 인디펜던트 할때 )
Physics/Quantum/Solid/Condensed2010. 4. 19. 20:51 |슈뢰딩거는 행렬역학이 줜나 짜증나서 슈뢰딩거 이퀘이션을 만들었다고 하는데, 쮸발, 슈뢰딩거 너도 짜증나긴 마찬가지다. 퍼터베이션 피터지게 하다보면, 가끔 이게 뭐하는 짓인가 싶을때가 있다. 뭔가 이렇게 해서는 안될 것 같은 느낌이랄까... 누구 말마따나 우리의 수학이 후지기 때문인거 같기도 하고...
암튼, 해밀토니안 연산자가 시간에 인디펜던트 하다는 조건 하에서, 오퍼레이터를 고정하고 스테이트의 타임 에볼루션을 살펴보자. 물론, 중학생도 이해할수 있도록 아주 쉽게 말이다.
우선 어떤 함수 f(x) 가 테일러 전개 가능하다고 하자. 알다시피 f(x)의 x' 을 중심으로한 테일러전개는 다음과 같다.
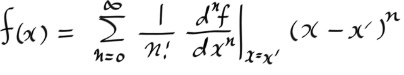
예를들어, 익스포넨셜 함수 f(x) = ex 를 0 을 중심으로 테일러 전개하면, ex = 1 + x/1! + x2/2! + ... 과 같이 된다.
이것으로 부터 영감을 얻어, 오퍼레이터에 대해서도 다음과 같이 정의하자.

이번에는 위의 테일러 전개식에서, x - x' 을 Δx 라고 놓자.
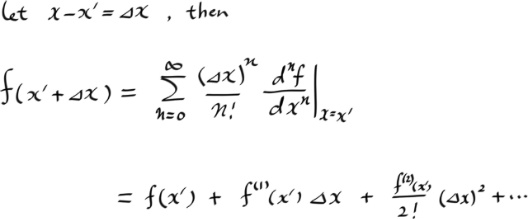
여기서 x' 은 아비트러리 하므로... 그걸 다시 x 로 잡아도 무관하다. ( 이것은 포인트와이즈 미분에서 도함수로 갈때 하던짓과 같다. )
그러면 다음과 같이 에러 전개할때 많이 쓰던 익숙한 버전을 얻는다. ( Δx 를 아주 작다면서 ε 따위로 놓고, 1차 혹은 2차 까지 근사하는 짓은 참 많이도 한다. )
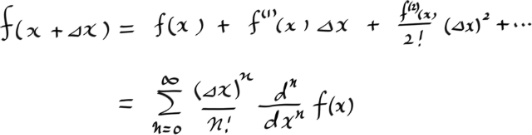
이제, 슈뢰딩거 이퀘이션의 해가 시간에 대해 테일러전개 가능하다고 하고, 위와같이 전개해보자.

이때, 우변의 시간 편미분 서메이션하는 부분은 연산자의 지수전개를 이용해 다음과 같이 쓸 수 있다.

따라서, 다음과 같이 웨이브펑션의 시간변화를 쓸 수 있다.

t = 0 으로 놓고, Δt 를 t 라고 놓으면, t=0 에서의 웨이브 펑션이 t 시간 후 어떻게 변하는가는 다음과 같이 된다.

양변에 포지션 아이겐 켓 을 곱해주면....

다음과 같이 슈뢰딩거 픽처를 얻는다.

같은 상황에서, 위식을 이용하면, 하이젠베르크 픽처도 쉽게 구할수있다. 허미션 컨주게이트가 i 부호만 바꿔주면 되니깐, 오퍼레이터 앞에 exp i ... 으로, 뒤에 exp -i ... 으로 된거 곱해지면 되겠다.
암튼, 해밀토니안 연산자가 시간에 인디펜던트 하다는 조건 하에서, 오퍼레이터를 고정하고 스테이트의 타임 에볼루션을 살펴보자. 물론, 중학생도 이해할수 있도록 아주 쉽게 말이다.
우선 어떤 함수 f(x) 가 테일러 전개 가능하다고 하자. 알다시피 f(x)의 x' 을 중심으로한 테일러전개는 다음과 같다.
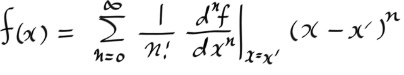
예를들어, 익스포넨셜 함수 f(x) = ex 를 0 을 중심으로 테일러 전개하면, ex = 1 + x/1! + x2/2! + ... 과 같이 된다.
이것으로 부터 영감을 얻어, 오퍼레이터에 대해서도 다음과 같이 정의하자.

이번에는 위의 테일러 전개식에서, x - x' 을 Δx 라고 놓자.
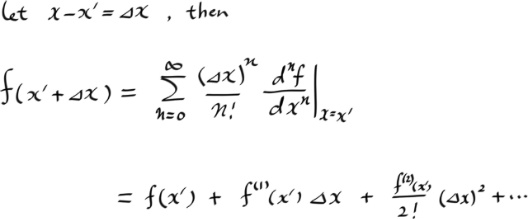
여기서 x' 은 아비트러리 하므로... 그걸 다시 x 로 잡아도 무관하다. ( 이것은 포인트와이즈 미분에서 도함수로 갈때 하던짓과 같다. )
그러면 다음과 같이 에러 전개할때 많이 쓰던 익숙한 버전을 얻는다. ( Δx 를 아주 작다면서 ε 따위로 놓고, 1차 혹은 2차 까지 근사하는 짓은 참 많이도 한다. )
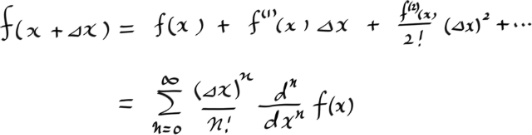
이제, 슈뢰딩거 이퀘이션의 해가 시간에 대해 테일러전개 가능하다고 하고, 위와같이 전개해보자.

이때, 우변의 시간 편미분 서메이션하는 부분은 연산자의 지수전개를 이용해 다음과 같이 쓸 수 있다.

따라서, 다음과 같이 웨이브펑션의 시간변화를 쓸 수 있다.

t = 0 으로 놓고, Δt 를 t 라고 놓으면, t=0 에서의 웨이브 펑션이 t 시간 후 어떻게 변하는가는 다음과 같이 된다.

양변에 포지션 아이겐 켓 을 곱해주면....

다음과 같이 슈뢰딩거 픽처를 얻는다.

같은 상황에서, 위식을 이용하면, 하이젠베르크 픽처도 쉽게 구할수있다. 허미션 컨주게이트가 i 부호만 바꿔주면 되니깐, 오퍼레이터 앞에 exp i ... 으로, 뒤에 exp -i ... 으로 된거 곱해지면 되겠다.
