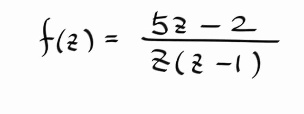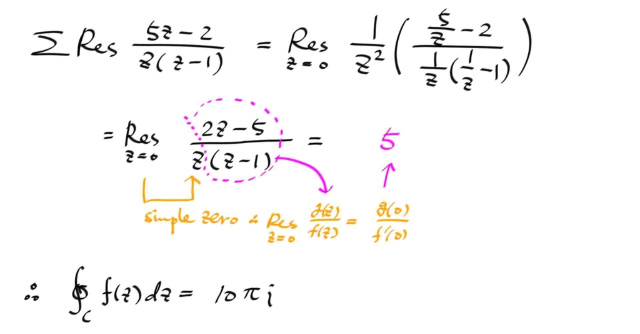[복소변수함수] Single Residue Method ( as the sum of all finitely many residues )

f(z)의 싱귤러 포인츠가 유한개이고, 컨투어가 그것들을 모두 감싸고 있을때, 레지두 정리는 각각의 싱귤러 포인트에서 레지두를 구할것을 요구한다.

하지만, f(z)를 약간 변형해서, 레지두 한개로 적분을 계산하는 방법이 있다.


싱귤러 포인트가 유한개이므로, 그것을 감싼 컨투어 C 는 바운디드 되어있고, 따라서, 원점에서 충분한 반경 r 에 의해 C 를 포함하는 원 C_r 을 생각할 수 있다. 그러면, 코시-구르사 정리에 의해, C 에 대한 적분이나, C_r 에 대한 적분이나 같다.


f(z) 가 ,  r < |z| < ∞   에서 어낼러틱하므로, 그것을 수렴영역으로 하는 중심 0 의 로렌트 시리즈가 존재한다. 그리고 항별적분하면 다음과 같이 된다.



그런데 살아남은 -1 차항의 계수는 0 에서의 레지두가 아니다. 우선 0 이 싱귤러 포인트인지 아닌지도 모르고, 게다가 수렴영역이 0 만 구멍이 뚤린 punctured disk 가 아니기 때문이다.


이제 , f(z) 에서 z 대신 1/z 을 대입하고, 전체를 z² 으로 나누면, z = 0 은 싱귤러 포인트가 되고 ( 물론, 리무버블이 되면, 테일러가 된다 ) , 변형된 함수의 0 을 중심으로 한 로렌트 전개의 수렴영역도 0 만 구멍난 punctured disk 가 된다. 게다가, 같은 계수가 여전히 -1 차 항의 계수가 된다.




즉,  r < |z|  < ∞   을 수렴영역으로 해서 , f(z) 의 로렌트 시리즈의 -1 차 항의 계수는 , f(1/z) / z²  의 0 에서의 레지두 인것이다.


또한, 그것은 결과적으로, f(z) 가 유한개의 싱귤러 포인트를 갖을때, 모든 레지두를 더한 값과 같다.

--------------------------------------------------------------------------------------------------



예제를 풀어보자.

이 함수를 적분하는데, 컨투어가 싱귤러 포인트 0 과 1 을 모두 감싼다고 하자. 그러면 레지두값을 모두 더한 값은 아래와 같이 구할수 있다. 특히, 분모가 0 에서 싱글 제로를 갖으므로, 분모와 분자를 잘 설정하면, 분모를 미분해서 날려버리고, 분자에 z=0 을 대입함으로써 레지두값이 나온다. 그러므로 적분값도 구해진다.