[복소변수함수] Zeros & Poles ( 영점과 극점 )

제로(zero) 는 복소함수를 0 으로 만드는 점들을 말한다. 번역은 영점이라고 하는듯. 폴(pole) 은 극점이라고 하고...


아무튼, 제로에도 오더를 주는데, 대충 중복도의 느낌으로... ( z - z₀ )  이런 때의 제로 z₀ 를 오더를 1 이라고 한다면, ( z - z₀ )^m  으로 m 번 중복된 제로 z₀ 를 오더 m 으로 생각하는 식이다.


같은 맥락인데, 함수가 어낼러틱해서 미분이 가능할때, 제로 오브 오더 m 을 다음과 같이 정의한다.

오더가 1 일때, 심플 제로 라는 표현을 쓰기도 하는데.. 잘 쓰지는 않는듯.


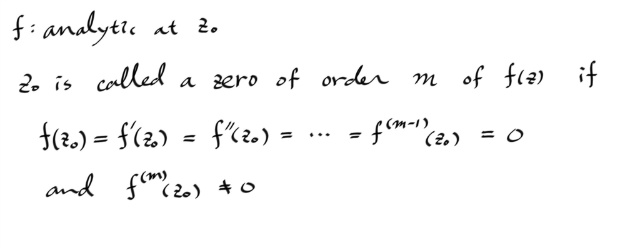
폴 오브 오더 m 에서 어낼러틱 펑션 나누기 ( z - z₀ )^m  에 대한 정리에 대응하는 , 제로에 대한 정리가 있는데, 어낼러틱 펑션 곱하기 ( z - z₀ )^m 으로 쓰는 방법이다.

-------------------------------------------------------------------------------------------------------
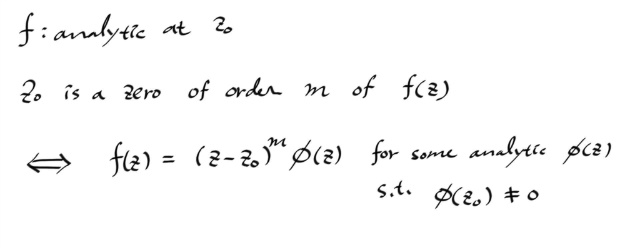
( Φ(z) 는 z0 에서 어낼러틱  )


증명은 => 방향과 <= 방향을 따로하자.


우선 => 방향.

f 가 z₀ 에서 어낼러틱하므로 z₀ 를 중심으로 테일러 전개하고, z₀ 에서 제로 오브 오더 m 을 갖으므로, f 에 z₀ 를 넣은것, f' 에 z₀ 를 넣은것, f'' 에 z₀ 를 넣은것 , ... , m-1 번 미분한것 까지 z₀ 를 넣으면 0 이 되는데, 이것은 m-1 승 텀에 대응하는 테일러 계수까지 모두 0 이 됨을 의미한다. 대신 그다음 테일러 계수는 0 이 아니다.

그러므로 남는 텀들은 모두 ( z - z₀  )^m  이상의 항들이므로, 그것으로 묶어낼수가 있다. 묶어내고 남은 시리즈는 어낼러틱 펑션이고, 거기에 z₀ 를 넣었을때 0 이 안되고 살아남는 상수텀이 아까 그 0 아니었던 테일러계수임.


<= 방향은... 계속 미분하면서 z₀  를 대입하면 계속 0 이다가, m 번 미분해야 비로소 0 이 아니게 됨.


------------------------------------------------------------------------------------------------------

예를 들어, f(z)  =  z ( e ^z  - 1  ) 라고 하면...

f(0 ) =  0  이고, 한번 미분한다음 0 을 대입해도 0 이고, 두번미분하고 0 을 넣으면 0 이 아니다. 그래서 f(z) 는 0 에서 오더 2 의 제로를 갖는다. 따라서 위 정리에 의해 z² 곱하기 어낼러틱 펑션의 곱으로 써져야 하므로, z² 을 앞으로 빼내면, Φ(z) = ( e ^z  - 1  ) / z  가 남는다. 그러나 이렇게 쓰면 z = 0 에서 정의되지 않고, Φ(z) 를 0 에서는 1 이 되도록 정의해주면 0 에서도 어낼러틱해진다.



-------------------------------------------------------------------------------------------------------


이번에는 제로 오브 오더 m 을 갖는 함수를 분모로 보내서, 폴 오브 오더 m 을 갖게 하는 것에 대해서 살펴보자.

어찌보면 매우 당연한 내용인데, 분자가 z_o 에서 0 이 안되도록 셋팅해놓은 이유는 그렇게 되면, 폴의 오더를 깎아먹기 때문이다.

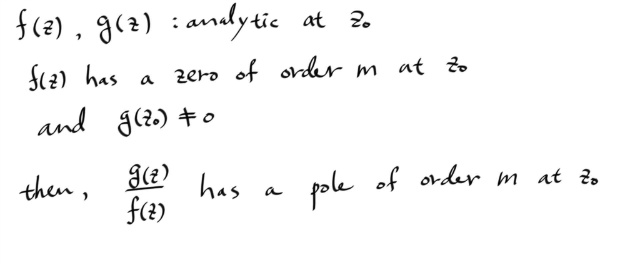
앞의 정리를 그대로 쓰고, 그걸로 나누면 되므로, 증명은 생략한다.



아무튼, g(z) / f(z) 가 폴 오브 오더 m 을 갖으므로, 이것은 다시 어낼러틱 펑션을 분자에 두고, ( z - z₀ )^m 을 분모에 두는 형태로 써진다.

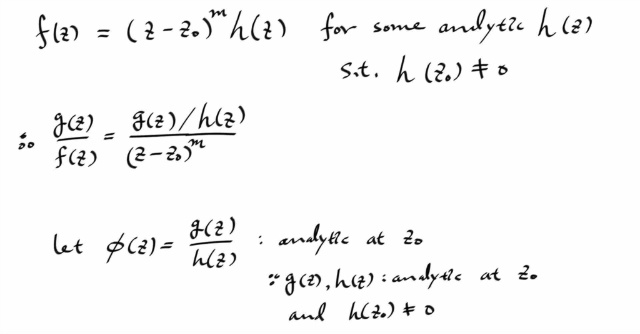
이제, 여기에 다시 Residue at pole 에 대한 정리를 쓸 수 있다.

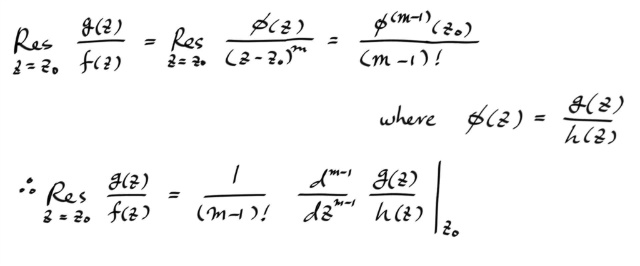
이것은 매우 번거롭고 지저분한 공식으로 실제적인 쓸모는 별로 없고, 분모식의 제로의 오더가 1 일 때, 굳이 부르자면 심플 제로일때, 상당히 프랙티컬한 공식을 얻을 수 있다.


f(z) 제로 z₀ 가 심플 제로라서,  g(z)/f(z) 가 심플 폴을 갖는다면, 아래와 같이 될 것이다.

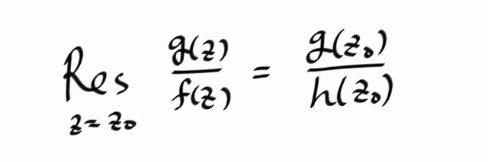
이때, 제로의 오더가 1 이므로,   f(z) 와 h(z) 의 관계는 단지 (z - z₀ ) 가 곱해진 차이밖에 없으므로, 양변을 미분하고 z₀  를 대입하면, 다음과 같은 공식을 얻을 수 있다.

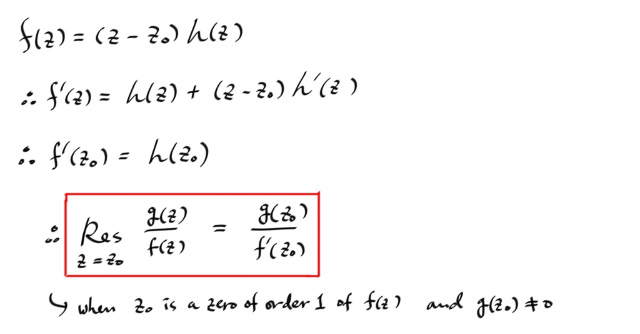
주의: 마지막 공식은 분모가 z0 에서 심플 제로를 갖을때만 사용할 수 있다.


-------------------------------------------------------------------------------------------------


예제를 풀어보자.

문제. cot z 를 반경 4 이고 중심이 원점인 원위에서 적분해라. ( 반시계방향 )

풀이.

컨투어 안에 들어간 싱귤러 포인트가 3개 이므로, 각각에서의 Residue 값을 구해서, 더하고, 2 π i 를 곱하면 된다. 그러므로, 레지두 구하는게 우선인데, 싱귤러 포인트들이 모두 심플 폴 들이다. 따라서 앞에서의 공식으로 레지두를 간단히 구할 수 있고, 그리고 나서 레지두 띠어럼을 쓰면 적분값을 쉽게 구할 수 있다.

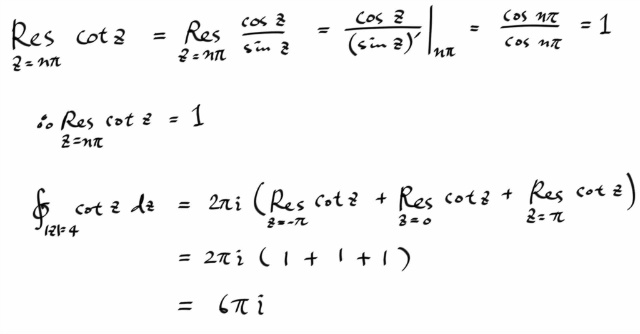
자, 이제 tan z 를 반지름 2 이고 중심이 원점인 원 ( 반시계방향 ) 위에서의 적분값은 암산으로도 구할 수 있다.

암산으로 구해보자면...

tan = sin / cos 이고, 컨투어 안에 들어가는 싱귤러 포인트는 π/2 , -π/2 로 두개이다. 각각 분모의 심플 제로이고, 따라서 분모미분하고, 분모분자에 그값들 집어넣으면 각각의 점에서 레지두값이 나오는데, 분모 미분하면 - sin z 이므로, 레지두값은 항상 -1 이다.

컨투어 안에 들어간게 2개 라고 했으므로, 2πi * ( -2 ) = - 4 π i  가 된다.