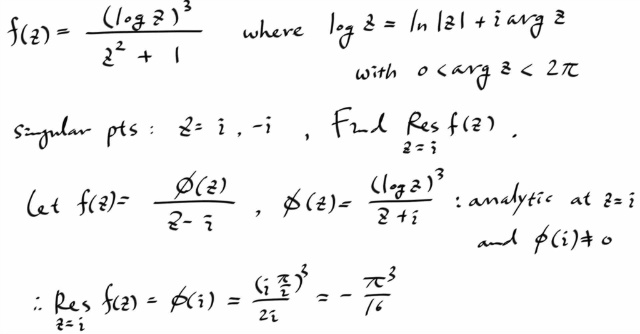[복소변수함수] Residues at Poles

레지두에 대한 이야기를 더 전개하기 위해서, 우리는 isolated 싱귤러 포인트를 분류하려고 한다.

특히, 로렌트 시리즈의 음의지수 파트의 형태를 가지고 분류를 하는데, 그 음의지수 파트를 간단히 principal part of f at z0 라고 부르자
( when f 를 싱귤러 포인트 z0 를 중심으로 로렌트 전개했을때... )

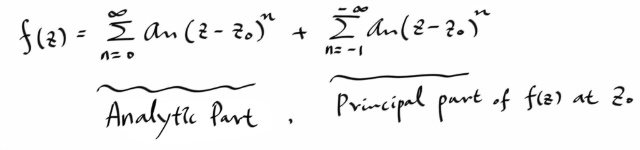
프린서펄 파트에 의한 isolated 싱귤러 포인트는 다음과 같이 세가지로 분류할 수 있다. ( 여기서는 그것들의 본질적인 성질을 다루는것은 아니다. 가령 pole 을 왜 pole 이라고 부르는지 따위에 대해서는 나중에 더 생각해보자. )

1. pole
2. removable singular point
3. essential singular point


1. pole
pole 은... f(z) 를 isolated singular point z0 를 중심으로 로렌트 전개했을때, 프린서펄 파트가 있으나 유한개일 때를 말한다.
principal part 가 m 개일때, z0 를 pole of order m 이라고 부르고, 오더가 1 일때를 보통 simple pole 이라고 부른다.
예) sinh z / z^4   은 폴 오브 오더 3 at z=0 , with residue 1/6 를 갖는다.

2. removable singular point
어떤 경우에 f(z) 가 z0 에서 싱귤러리티를 갖음에도 불구하고, 막상 전개해보면 프린서펄 파트가 없을때를 말한다. (즉, 대응되는 계수가 전부 0 이 되어버림 )
이러한 싱귤러 포인트들은 f(z0) 를 재정의 해줌으로써 제거가 가능하다. 리무버블 싱귤러 포인트인 경우에는 레지두는 당연히 0 이다.
예) ( 1 - cos z ) / z^2   은 z=0 에서 리무버블 싱귤러 포인트를 갖고, f(0) = 1/2 로 redefine 해주면, f 는 entire 해진다.

3. essential singular point
이건 프린서펄 파트가 무한개일 때를 말한다.
예) exp ( 1/z ) 는 z=0 에서 이센셜 싱귤러 포인트를 갖는다. with residue = 1 .



---------------------------------------------------------------------------------------------------------
이제 isolated 싱귤러 포인트가 폴인 경우에 대해 좀 더 살펴보자.

---------------------------------------------------------------------------------------------------------
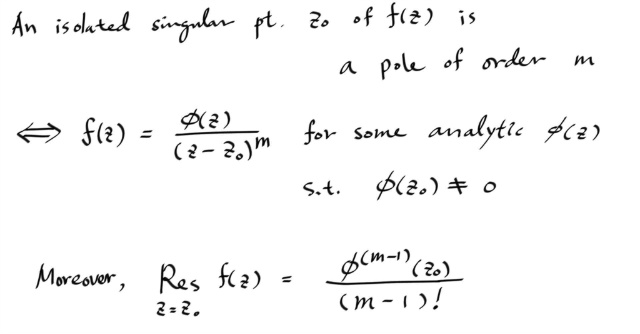
( Φ(z) 는 z0 에서 어낼러틱  )


우선. => 방향 증명부터...

zo 가 폴 오브 오더 m 이면, zo 를 중심으로 하는 어떤 punctured disk 에서, z0 를 중심으로 다음과 같은 로렌트 시리즈를 갖는다.

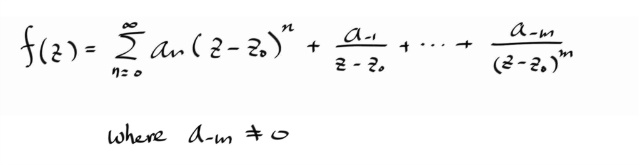
(z-z0)^m 으로 통분하면...

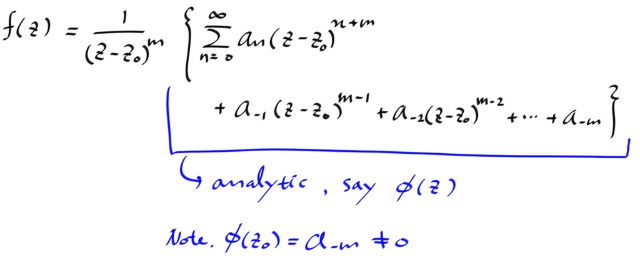
<= 방향 증명은... 분자의 Φ(z) 가 어낼러틱하므로, 테일러 전개한다음, 분모 (z-z0)^m 으로 나누면 쉽게 보일 수 있다.

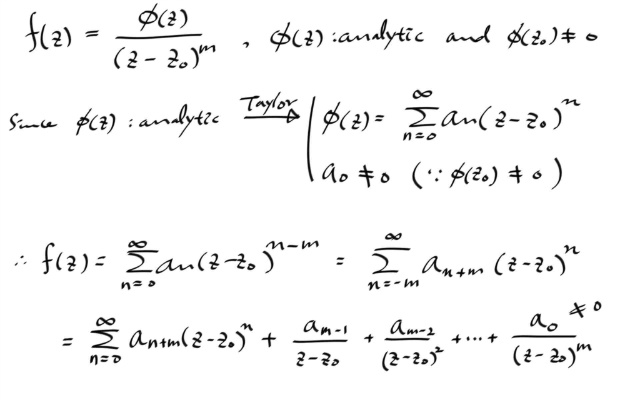
특히, 이렇게 전개된 상태에서, Residue 는 a_m-1 이므로, 이것을 구하면 된다. 이것은 단지 Φ(z) 의 m-1 승 텀의 테일러 계수일 뿐이다. 즉, 아래의 결과는 당연하다.

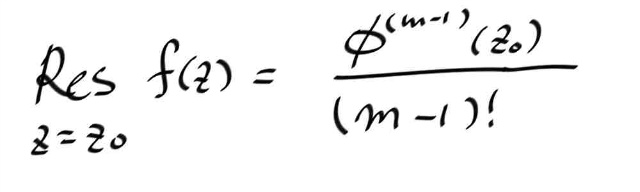
특히, 심플 폴일때 , 즉 m=1 일때는, 레지두 값이 그냥 분자함수에 z0 를 대입한것과 같아진다. 단, 0 이 아니어야 한다.


------------------------------------------------------------------------------------------------------


예제를 풀어보자.