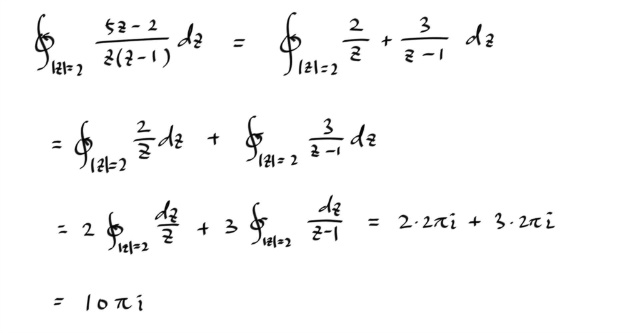Cauchy's Residue Theorem ( 유수 정리 )
Math/Complex2009. 7. 29. 10:06 |코시 인테그랄 포뮬러를 다시 살펴보자.
코시 인테그랄 포뮬러의 적분식을 보면, f(z)/(z-w) 형태인데, 특히 f가 어낼러틱해서, 컨투어에 의해 감싸진 영역에서는 싱귤러 포인트는 w 하나만 갖게 된다.
컨투어 내부에 싱귤러 포인트가 한개가 아니라 몇 개가 있는 경우에는 path deformation 을 해주면 되는데, 각 싱귤러 포인트들을 하나씩만 감싸는 작은 컨투어들을 잡으면 ( 당연히 positively oriented 로 다가.. ) 결과적으로 각 컨투어들에 대해서 적분한것들의 합이 전체를 감싼 컨투어 인테그랄과 같게 된다 by Cauchy-Goursat Thm.
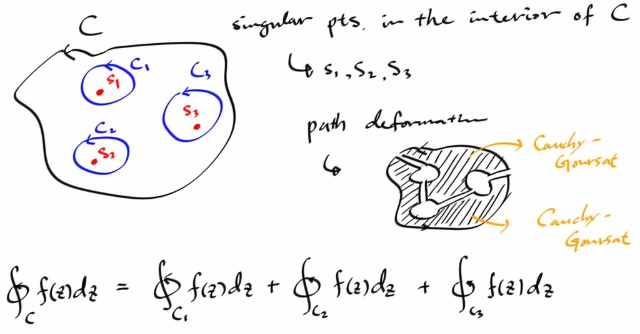
그러니까, 각각의 싱귤러 포인트를 하나씩만 감싼 컨투어 인테그랄을 코시 적분공식으로 구해서 더하면 되는데, 그럴려면 각 싱귤러 포인트들이 독립적으로 한개씩 찢어져 있어야 한다는 말이 된다.
즉, 두개의 싱귤러 포인트가 무한히 가깝게 붙어있어서 아무리 작은 네이버후드를 잡아도 한놈만 포함할수 없는 지경이라면, 코시 적분공식을 쓸수가 없는 것이다. ( 물론, 달랑 두개로는 이런짓을 할 수 없다. )
아무튼, 우리의 전략이 요구하는 바는, 싱귤러 포인트들이 각각 따로 따로 하나씩 떨어져있어야 한다는 것이다.
조금더 정제해서 타펄롸지컬리 표현하자면, f(z)의 모든 싱귤러 포인트들의 집합을 S 라고 할때, 우리가 적분하고자 하는 컨투어에 의해 감싸져 있는 싱귤러 포인트들 ( 당연히 S 의 원소들이다 ) 이 S 의 리미트 포인트가 아니어야 한다. 즉, isolated points of S 여야 한다는 거다.
S의 리미트 포인트 라면, 아무리 그 싱귤러 포인트를 중심으로 네이버후드를 잡아도, 항상 다른 싱귤러 포인트를 포함하게 되므로, 한 놈만 감싸는 그런 컨투어는 잡을 수가 없다. 반대로, limit point of S 가 아니라면, ( 즉, isolated pt of S 라면 ) 그 싱귤러 포인트만을 포함하는 네이버후드가 존재하고, 따라서 그 네이버후드의 바운더리를 컨투어로 잡으면 원하는 목적을 달성할수 있게된다.
참고로 S가 리미트 포인트를 갖으려면, S가 무한집합이어야 하므로, 싱귤러 포인트가 고작 유한개인 경우는 무조건 isolated singular point 들 밖에 갖을 수 없다.
-----------------------------------------------------------------------------------------------------------
이제 f(z) 를 컨투어 C 에 대해서 적분하려고 할때, C 내부에서 f(z) 가 싱귤러 포인트 몇개를 갖는다고 하자. 즉, 모두 isolated singular points 들이다.
이제, 각각의 싱귤러 포인트들을 하나씩만 감싸는 컨투어를 잡은다음 각각 적분값을 더하면 그만인데, 문제는, 코시 적분공식을 쓰려면 싱귤러 포인트 s 에 대해 1 / ( z - s )^n 따위의 항을 가지고 있어야 한다는 것이다.
방법은, 적분하려고 하는 함수 f(z) 를 싱귤러 포인트 s 를 중심으로 로렌트 전개하면 1/(z-s)^n 과 같은 항들이 나오게 되고, f(z)의 적분을 로렌트 시리즈의 항별적분으로 ( 유니폼 컨버전스 이야기는 생략한다. ) 계산하는데, 이것을 코시 적분공식으로 하는 것이다.
싱귤러 포인트 s가 isolated 되어 있으면, s를 중심으로한 f(z)의 로렌트 시리즈는, s만 포함하도록 잡은 컨투어를 포함하는 punctured disk ( 0 < |z-s| < r ) 를 도메인으로 해서 전개된다. 물론, punctured disk의 구멍은 그 싱귤러 포인트 s 가 된다.
예를들어, exp ( 1/z ) 를 중심이 원점인 원 위에서 적분한다고 하자. (말없으면 ccw)
exp (1/z) 는 원점에서만 싱귤러 포인트를 갖으므로, 당연히 isolated 되어있고, 이것을 원점에 대해서 로렌트 전개한후에, 항별적분한다.
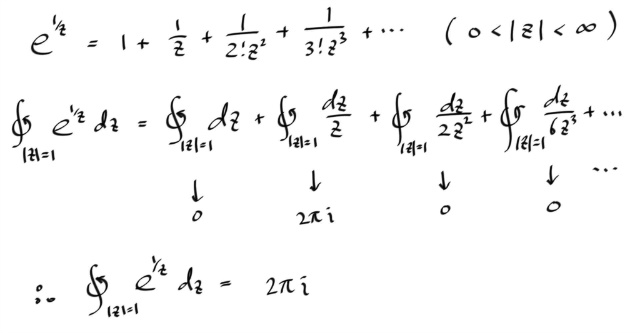
우변의 두번째 적분을 제외한 모든 적분항은 0 이 되는데, 그것은 적분하고자 하는 컨투어위와 내부에서 모두 역도함수를 갖기 때문이다. 역도함수를 갖으면, 적분이 경로에 무관해지고 따라서 closed contour 에 대한 적분은 0 이다.
반면, 두번째 항은 브랜치 컷에서 역도함수를 갖는데 실패하므로, 0 이 된다고 말할수 없고, 간단히 코시 인테그랄 포뮬러에 의해 2 π i 가 된다. 물론, 세번재항 이후의 적분들은 , 제너럴 라이즈드 코시 인테그랄 포뮬러를 쓰면 모두 0 이 됨을 확인 할 수 있다.
위의 느낌을 좀 더 진행시키면, f(z) 의 어떤 isolated 싱귤러 포인트 zo 를 하나만 감싸는 simple closed contour C 에 대한 적분을 살펴보자.
그럼 앞에서 한것처럼 , 중심이 z0 인 punctured disk 를 C 를 포함해서 잡는다. 물론, 다른 싱귤러 포인트는 들어가지 않도록... 그래서 그 영역을 수렴영역으로 해서, z0 를 중심으로 하는 f(z) 의 로렌트 전개를 하고, 제너럴라이즈드 코시 적분공식으로 항별 적분하면...
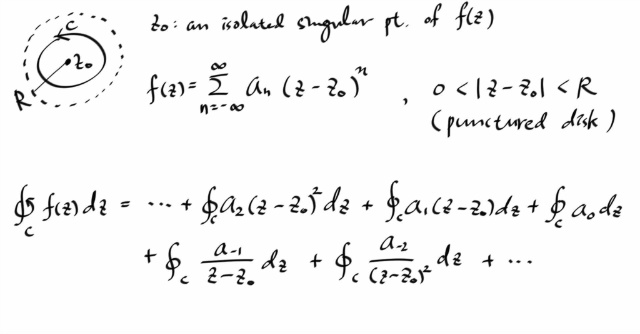
로렌트 시리즈의 각 계수는 상수들 이므로, 적분기호 밖으로 빼고, 지수가 nonnegative 인 항들의 적분은 모두 0 이된다. ( 피적분함수가 해당영역에서 모두 어낼러틱함 , 따라서 Cauchy-Goursat 에 의해 적분은 0 )
지수가 -1 보다 작은 텀들, -2 , -3 , -4 , .. 들도 모두 적분은 0 이다. 제너럴 라이즈드 코시 인테그랄 포뮬러를 쓰면 상수를 미분해야 되므로, 모두 0 이다.
따라서, 다 죽고, 지수가 -1 인 항의 적분만 남는다. 이런 젼차로, 그 계수를 f(z)의 z0 에서의 Residue 라고 부른다. 번역 용어로는 "유수" 라고 부른다고 한다.
레지두(residue) 의 정의는 다음과 같다.
복소함수 f(z) 를 isolated 싱귤러 포인트 s 하나를 중심으로 punctured disk 에서 로렌트 전개했을때,
-1 차항의 계수를 f 의 s 에서의 레지두 라고 부른다.
그리고, 레지두와 함께 살아남은 적분항의 값은 2 π i 이므로, 좌변의 적분값은 Residue * 2 π i 가 된다.
따라서, 일반적으로, 싱귤러 포인트 하나만 감싸는 컨투어에 대한 적분은 다음과 같다고 할 수 있다.
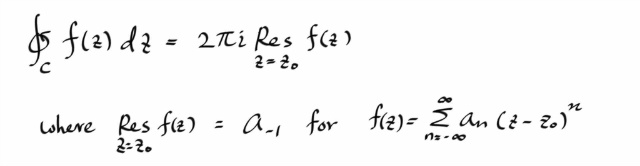
그러므로, 맨 처음에 했던 이야기와 접목시키면... 컨투어 내부에 유한개의 isolated 싱귤러 포인트들이 있을때, 각각의 싱귤러 포인트 한개씩만 감싸는 컨투어들에 대해서 residue 값으로 적분값을 구한다음 모두 더하면, 원래의 컨투어에 대한 적분값이 나올것이므로... 다음의 Cauchy's Residue Theorem 을 얻는다.
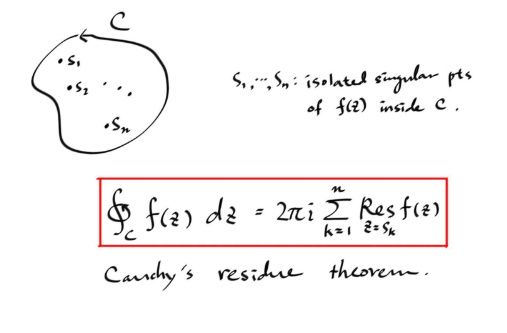 Residue 를 나타내는 기호가 two line 노테이션이라서, 타자로 칠때 좀 불편하므로, 종종 Res( f ; s0 ) 따위의 노테이션을 쓰도록 하겠다. 뜻은 똑같다. f 의 s0 에서의 레지두. ( 참고로, 꼭 positively oriented simple closed contour 가 아니더라도, 가령 반대로 돈다던가 하면, 그땐 2 π i 대신 - 2 π i 이므로, - 부호만 써주면 된다. )
Residue 를 나타내는 기호가 two line 노테이션이라서, 타자로 칠때 좀 불편하므로, 종종 Res( f ; s0 ) 따위의 노테이션을 쓰도록 하겠다. 뜻은 똑같다. f 의 s0 에서의 레지두. ( 참고로, 꼭 positively oriented simple closed contour 가 아니더라도, 가령 반대로 돈다던가 하면, 그땐 2 π i 대신 - 2 π i 이므로, - 부호만 써주면 된다. )
-----------------------------------------------------------------------------------------------------
예제를 풀어보자.
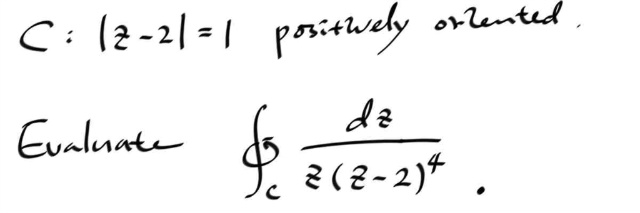
피적분 함수의 싱귤러 포인트는 원점과 z=2 인데, 적분하고자 하는 컨투어 내부에 들어간 싱귤러포인트는 z=2 밖에 없다.
피적분함수를 z=2 를 중심으로 로렌트 전개하고, 레지두를 구한다음, 2 π i 를 곱하면, 적분값을 계산할 수 있다.
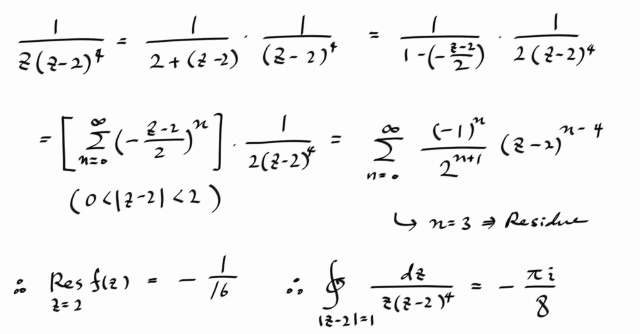
같은 계산을 이번에는, 코시 인테그랄 포뮬러로 구해보자. 왜냐면 컨투어 내부에 싱귤러 포인트가 하나밖에 없으으니까...
피적분함수의 분모를 z-4 의 4승 으로 보고, 분자 g(z) = 1/z 라고 하면, 이 적분값은 1/z 를 3번 미분하고, z=2 를 대입한 후에, 3 ! 로 나누고, 2 π i 를 곱해주면 된다.
1/z 를 세번 미분하면... -6 z^(-4) 이고, z=2 를 대입하면... -6 * (1/16) 이된다. 이걸 3 ! 로 나누면... - 1/16 이 되고... 여기에 2 π i 를 곱하면, - π i / 8 로 동일한 답이 나온다.
-----------------------------------------------------------------------------------------------------
이번에는 컨투어 안에 두개의 싱귤러 포인트가 있는 경우를 적분해보자.
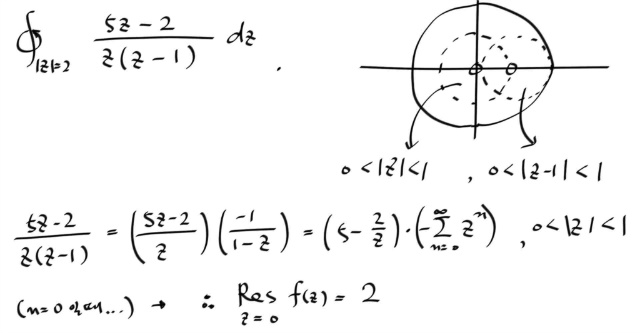
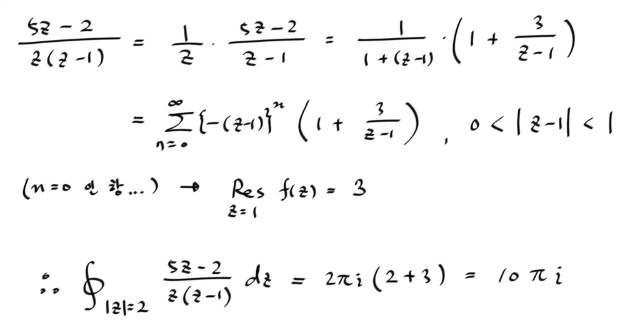
참고로 이경우에는, 부분분수로 쪼개서 푸는게 더 쉽다.
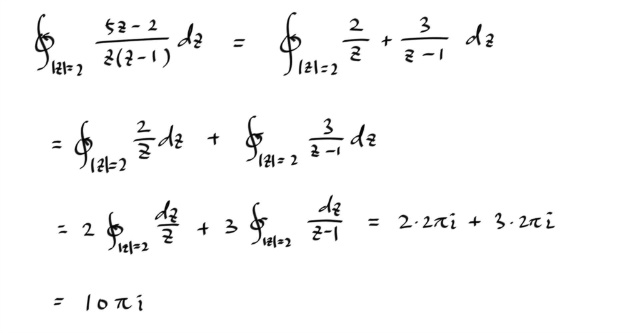
코시 인테그랄 포뮬러의 적분식을 보면, f(z)/(z-w) 형태인데, 특히 f가 어낼러틱해서, 컨투어에 의해 감싸진 영역에서는 싱귤러 포인트는 w 하나만 갖게 된다.
컨투어 내부에 싱귤러 포인트가 한개가 아니라 몇 개가 있는 경우에는 path deformation 을 해주면 되는데, 각 싱귤러 포인트들을 하나씩만 감싸는 작은 컨투어들을 잡으면 ( 당연히 positively oriented 로 다가.. ) 결과적으로 각 컨투어들에 대해서 적분한것들의 합이 전체를 감싼 컨투어 인테그랄과 같게 된다 by Cauchy-Goursat Thm.

그러니까, 각각의 싱귤러 포인트를 하나씩만 감싼 컨투어 인테그랄을 코시 적분공식으로 구해서 더하면 되는데, 그럴려면 각 싱귤러 포인트들이 독립적으로 한개씩 찢어져 있어야 한다는 말이 된다.
즉, 두개의 싱귤러 포인트가 무한히 가깝게 붙어있어서 아무리 작은 네이버후드를 잡아도 한놈만 포함할수 없는 지경이라면, 코시 적분공식을 쓸수가 없는 것이다. ( 물론, 달랑 두개로는 이런짓을 할 수 없다. )
아무튼, 우리의 전략이 요구하는 바는, 싱귤러 포인트들이 각각 따로 따로 하나씩 떨어져있어야 한다는 것이다.
조금더 정제해서 타펄롸지컬리 표현하자면, f(z)의 모든 싱귤러 포인트들의 집합을 S 라고 할때, 우리가 적분하고자 하는 컨투어에 의해 감싸져 있는 싱귤러 포인트들 ( 당연히 S 의 원소들이다 ) 이 S 의 리미트 포인트가 아니어야 한다. 즉, isolated points of S 여야 한다는 거다.
S의 리미트 포인트 라면, 아무리 그 싱귤러 포인트를 중심으로 네이버후드를 잡아도, 항상 다른 싱귤러 포인트를 포함하게 되므로, 한 놈만 감싸는 그런 컨투어는 잡을 수가 없다. 반대로, limit point of S 가 아니라면, ( 즉, isolated pt of S 라면 ) 그 싱귤러 포인트만을 포함하는 네이버후드가 존재하고, 따라서 그 네이버후드의 바운더리를 컨투어로 잡으면 원하는 목적을 달성할수 있게된다.
참고로 S가 리미트 포인트를 갖으려면, S가 무한집합이어야 하므로, 싱귤러 포인트가 고작 유한개인 경우는 무조건 isolated singular point 들 밖에 갖을 수 없다.
-----------------------------------------------------------------------------------------------------------
이제 f(z) 를 컨투어 C 에 대해서 적분하려고 할때, C 내부에서 f(z) 가 싱귤러 포인트 몇개를 갖는다고 하자. 즉, 모두 isolated singular points 들이다.
이제, 각각의 싱귤러 포인트들을 하나씩만 감싸는 컨투어를 잡은다음 각각 적분값을 더하면 그만인데, 문제는, 코시 적분공식을 쓰려면 싱귤러 포인트 s 에 대해 1 / ( z - s )^n 따위의 항을 가지고 있어야 한다는 것이다.
방법은, 적분하려고 하는 함수 f(z) 를 싱귤러 포인트 s 를 중심으로 로렌트 전개하면 1/(z-s)^n 과 같은 항들이 나오게 되고, f(z)의 적분을 로렌트 시리즈의 항별적분으로 ( 유니폼 컨버전스 이야기는 생략한다. ) 계산하는데, 이것을 코시 적분공식으로 하는 것이다.
싱귤러 포인트 s가 isolated 되어 있으면, s를 중심으로한 f(z)의 로렌트 시리즈는, s만 포함하도록 잡은 컨투어를 포함하는 punctured disk ( 0 < |z-s| < r ) 를 도메인으로 해서 전개된다. 물론, punctured disk의 구멍은 그 싱귤러 포인트 s 가 된다.
예를들어, exp ( 1/z ) 를 중심이 원점인 원 위에서 적분한다고 하자. (말없으면 ccw)
exp (1/z) 는 원점에서만 싱귤러 포인트를 갖으므로, 당연히 isolated 되어있고, 이것을 원점에 대해서 로렌트 전개한후에, 항별적분한다.
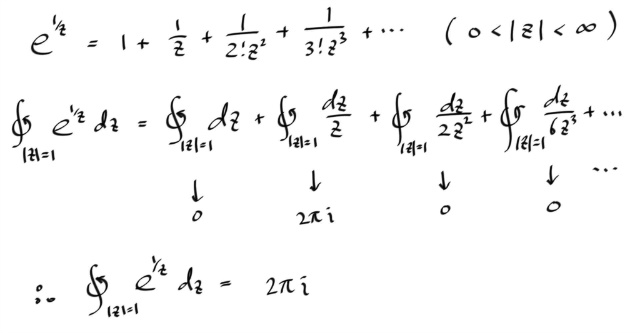
우변의 두번째 적분을 제외한 모든 적분항은 0 이 되는데, 그것은 적분하고자 하는 컨투어위와 내부에서 모두 역도함수를 갖기 때문이다. 역도함수를 갖으면, 적분이 경로에 무관해지고 따라서 closed contour 에 대한 적분은 0 이다.
반면, 두번째 항은 브랜치 컷에서 역도함수를 갖는데 실패하므로, 0 이 된다고 말할수 없고, 간단히 코시 인테그랄 포뮬러에 의해 2 π i 가 된다. 물론, 세번재항 이후의 적분들은 , 제너럴 라이즈드 코시 인테그랄 포뮬러를 쓰면 모두 0 이 됨을 확인 할 수 있다.
위의 느낌을 좀 더 진행시키면, f(z) 의 어떤 isolated 싱귤러 포인트 zo 를 하나만 감싸는 simple closed contour C 에 대한 적분을 살펴보자.
그럼 앞에서 한것처럼 , 중심이 z0 인 punctured disk 를 C 를 포함해서 잡는다. 물론, 다른 싱귤러 포인트는 들어가지 않도록... 그래서 그 영역을 수렴영역으로 해서, z0 를 중심으로 하는 f(z) 의 로렌트 전개를 하고, 제너럴라이즈드 코시 적분공식으로 항별 적분하면...
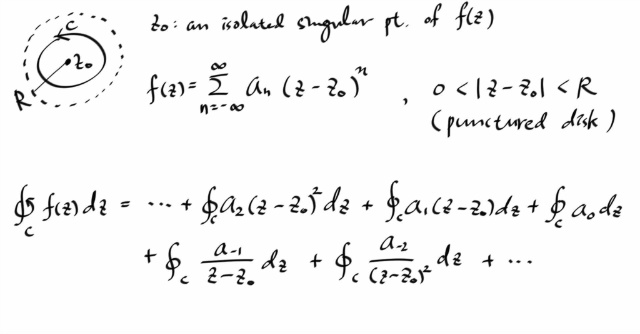
로렌트 시리즈의 각 계수는 상수들 이므로, 적분기호 밖으로 빼고, 지수가 nonnegative 인 항들의 적분은 모두 0 이된다. ( 피적분함수가 해당영역에서 모두 어낼러틱함 , 따라서 Cauchy-Goursat 에 의해 적분은 0 )
지수가 -1 보다 작은 텀들, -2 , -3 , -4 , .. 들도 모두 적분은 0 이다. 제너럴 라이즈드 코시 인테그랄 포뮬러를 쓰면 상수를 미분해야 되므로, 모두 0 이다.
따라서, 다 죽고, 지수가 -1 인 항의 적분만 남는다. 이런 젼차로, 그 계수를 f(z)의 z0 에서의 Residue 라고 부른다. 번역 용어로는 "유수" 라고 부른다고 한다.
레지두(residue) 의 정의는 다음과 같다.
복소함수 f(z) 를 isolated 싱귤러 포인트 s 하나를 중심으로 punctured disk 에서 로렌트 전개했을때,
-1 차항의 계수를 f 의 s 에서의 레지두 라고 부른다.
그리고, 레지두와 함께 살아남은 적분항의 값은 2 π i 이므로, 좌변의 적분값은 Residue * 2 π i 가 된다.
따라서, 일반적으로, 싱귤러 포인트 하나만 감싸는 컨투어에 대한 적분은 다음과 같다고 할 수 있다.
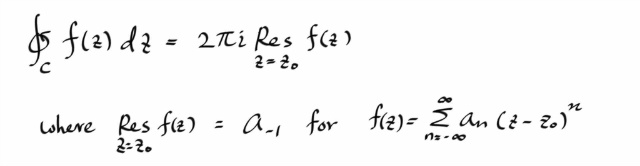
그러므로, 맨 처음에 했던 이야기와 접목시키면... 컨투어 내부에 유한개의 isolated 싱귤러 포인트들이 있을때, 각각의 싱귤러 포인트 한개씩만 감싸는 컨투어들에 대해서 residue 값으로 적분값을 구한다음 모두 더하면, 원래의 컨투어에 대한 적분값이 나올것이므로... 다음의 Cauchy's Residue Theorem 을 얻는다.
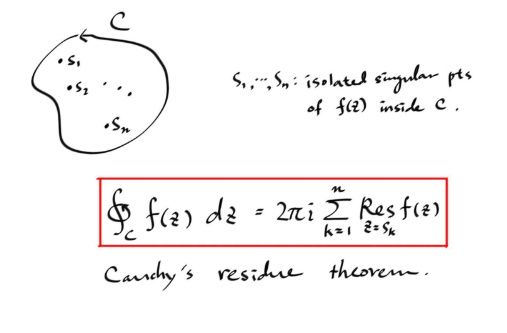
-----------------------------------------------------------------------------------------------------
예제를 풀어보자.
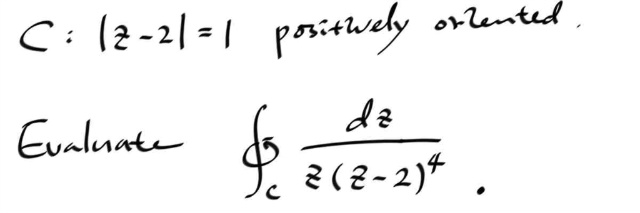
피적분 함수의 싱귤러 포인트는 원점과 z=2 인데, 적분하고자 하는 컨투어 내부에 들어간 싱귤러포인트는 z=2 밖에 없다.
피적분함수를 z=2 를 중심으로 로렌트 전개하고, 레지두를 구한다음, 2 π i 를 곱하면, 적분값을 계산할 수 있다.
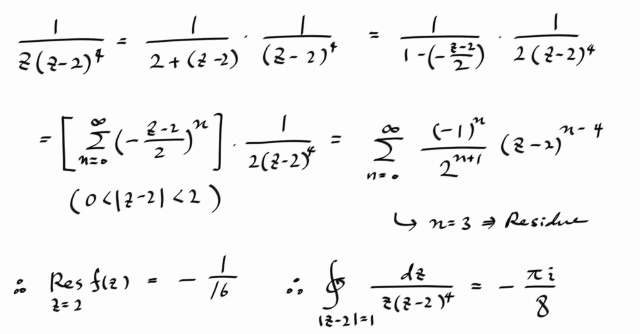
같은 계산을 이번에는, 코시 인테그랄 포뮬러로 구해보자. 왜냐면 컨투어 내부에 싱귤러 포인트가 하나밖에 없으으니까...
피적분함수의 분모를 z-4 의 4승 으로 보고, 분자 g(z) = 1/z 라고 하면, 이 적분값은 1/z 를 3번 미분하고, z=2 를 대입한 후에, 3 ! 로 나누고, 2 π i 를 곱해주면 된다.
1/z 를 세번 미분하면... -6 z^(-4) 이고, z=2 를 대입하면... -6 * (1/16) 이된다. 이걸 3 ! 로 나누면... - 1/16 이 되고... 여기에 2 π i 를 곱하면, - π i / 8 로 동일한 답이 나온다.
-----------------------------------------------------------------------------------------------------
이번에는 컨투어 안에 두개의 싱귤러 포인트가 있는 경우를 적분해보자.
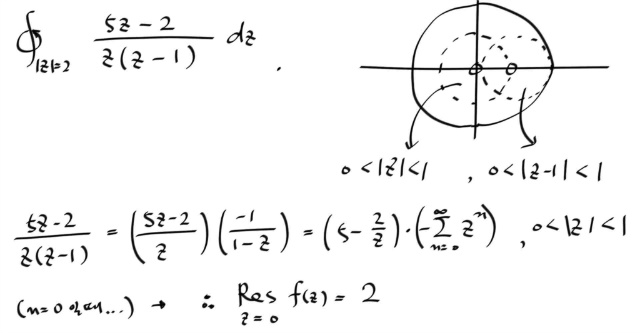
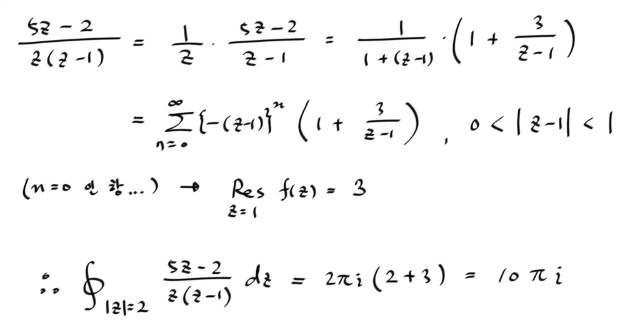
참고로 이경우에는, 부분분수로 쪼개서 푸는게 더 쉽다.