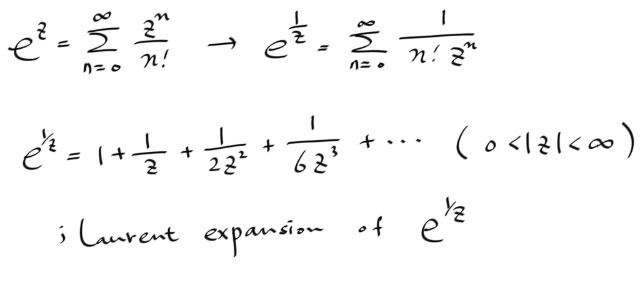[복소변수함수] Laurent Series (로렌트 급수, 로랑 급수)
Math/Complex2009. 7. 27. 10:25 |캘큘러스에서 배웠던 테일러 시리즈는 복소에서도 마찬가지로 유효하다.
대신, 수렴반경이 진짜 "반경" 이 된다. 그리고, 오픈디스크 내에서 holomorphic 이기만 하면 충분하다.
보통, 테일러 정리 증명은 시리즈의 파샬섬과 함수사이의 차이가 0 으로 다가간다는 것을 보이는 데, 우리는 그러한 엄밀한 방법 말고, 느낌만 얻을수 있는 스토리로 가자.
f(z) 가 중심이 원점이고, 반경 R 인 반시계방향으로 도는 컨투어 위와 안쪽에서 어낼러틱하다고 하자. 그러면 임의의 내부점 z 에 대해서 f(z) 는 코시 인테그랄 포뮬러에 의해 다음과 같이 쓸 수 있다.
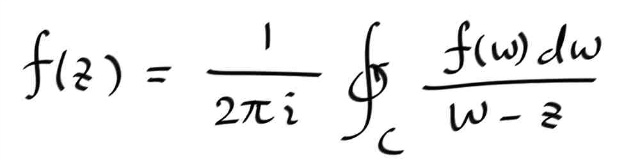
이때 피적분식에서 1 / ( w-z ) 를 기하급수로 전개하자.
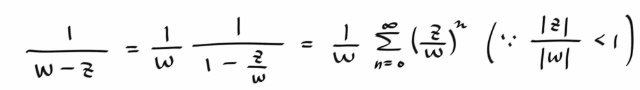
w 는 C 위에 있고, z 는 안쪽에 있으므로 수렴조건을 만족한다.
이제 서메이션 기호를 적분식 밖으로 빼자. 이때 요구되는 조건은 유니폼 컨버전스인데, 해석때 얘기하기로 하고, 된다고 치고 그냥 빼자.
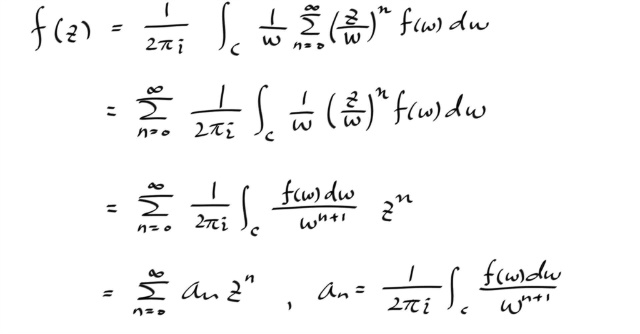
그런데, 계수 an 을 나타내는 적분식의 w 는 어차피 dummy variable 이므로, 아래와 같이 써도 된다.
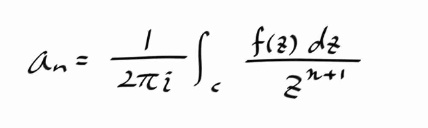단, 좌변의 f(z) 에서 z 는 도메인 내부점이어야 하지만, an 을 나타내는 적분식 안에 들어있는 f(z) 의 z는 더미 베리어블이므로, 좌변의 z와는 무관하다. 대신 적분경로에 드러나있듯이 C 상의 점들이다.
참고로 중심을 z0 로 쉬프트 시키고, 코시 적분공식을 쓰면, 원하는 결과를 얻는다.
----------------------------------------------------------------------------------------------------
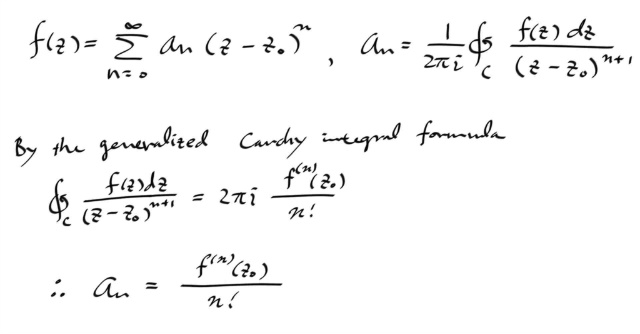
이제 로렌트 급수를 볼 차례이다.
미적시간의 기억을 되살려보자. 테일러 급수가 중심이 0 일때를 특히 맥로린 급수라고 했는데, 문제는 1/x 는 맥로린 급수로 전개할 수가 없다는 것이다. 1/x^2 도 마찬가지고, 1/x^3 도 마찬가지다. 즉, 저런녀석들은 0 에서 어낼러틱 하지 않다.
그러면, 임의의 함수를 1/x , 1/x^2 , 1/x^3 , ... 쪽으로도 전개하는 건 어떨까?
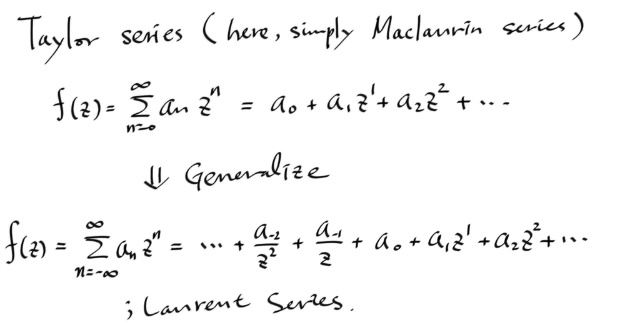
마찬가지로, 중심을 z0 로 쉬프트 시키면...
이제 할일은 계수를 계산하는 일 ( with 어떤 조건하에서... ) 이다.
로렌트 시리즈는 테일러 시리즈의 일반화로 생각될수 있으므로, 테일러 시리즈는 로렌트 시리즈에서 음수차수를 갖는 항들의 계수가 모두 0 인 특별한 케이스라고 말할 수 있다.
로렌트 시리즈에 대한 감을 얻기 위해, 직접 예를 하나 살펴보자.
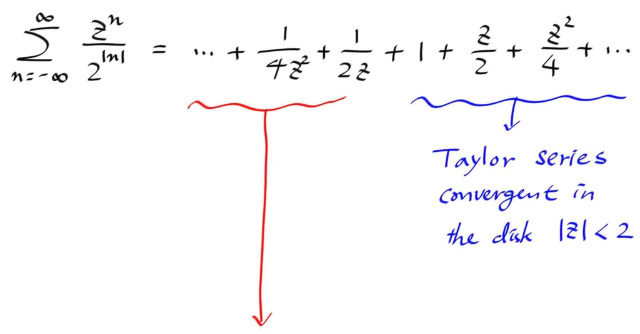
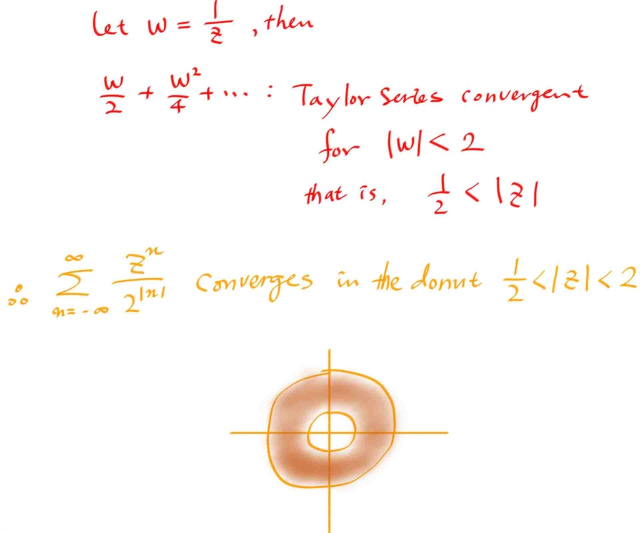
결과적으로, 로렌트 시리즈를 두 파트로 나누면, 양수 지수쪽은 반경 R 안쪽에서 수렴하는 테일러 급수고, 음수 지수쪽은 1/z = w 로 치환하면 역시 테일러급수이고, w가 반경 r 안쪽에서 수렴하는데, 다시 환원시키면 z 가 반경 r 바깥쪽에서 수렴하게 되어, 결국 위와같은 도넛모양의 수렴영역이 나오게 된다.
중심을 z0 로 이동시키면, 로렌트시리즈의 수렴영역은 보통 r < | z - z0 | < R 꼴이고, R 이 무한대 일수도 있고, r 이 0 일수도 있다. 물론 r=R 이 되어버린다던가 하면 테일러때도 그랬던 것처럼 수렴영역이 없어져버린다. 그리고, r = 0 인 경우, 수렴영역은 punctured disk 이다.
아무튼, 그래서 로렌트 시리즈는 다음과 같다.
일단 이것이 테일러 급수를 포함하는 개념인지 확인해보기 위해, 테일러급수의 상황, 즉, f 가 반경 R 안쪽에서 어낼러틱하다고 해보자. 즉 내부에 싱귤러 포인트가 없는경우다.
그러면, 음수지수에 대한 계수의 피적분식은 n=-k ( k ≥ 1 ) 라고 하면, f(z) / (z-z0)^(-k+1) 가 되고, 이것은 f(z) (z-z0)^(k-1) 이므로, 이 자체가 z0 에서도 어탤러틱하다. 따라서, 코시-구르사 정리에 의해 적분값은 0 이 된다. 즉, 음수 지수에 대한 계수들이 모두 0 이 되고, 곧 테일러 급수가 된다.
Note. 여기서 zo 는 도넛, 즉, 원의 중심이다. 그런데 f 는 도넛내부에서만 어낼러틱하면 되고, 도넛의 가운데 구멍영역에서는 어낼러틱하지 않아도 되는 상황이다. 그런데 z0 는 도넛의 중심이므로 도넛의 안쪽 구멍에 위치한다. 전개되는 항들을 보면 (z-z0) 의 음수지수들은 모두 z0 에서 어낼러틱하지 않다. 결국, 음수지수들은 z0 에 대해 어낼러틱하지 않은 텀들로 전개하고 있는것이다. 즉, 0에서 어낼러틱하지 않은 함수를 0 을 중심으로 전개할때, 중심에서 어낼러틱하지 않는 1/z , 1/z^2 , ... 들로 전개하는 것이다. (물론 양수지수 텀들에 추가적으로 ... )
아무튼 위의 정리가 사실이라면, 신기하게도 음수지수에 대한 계수도 양수지수에 대한 계수와 형식적으로 같은 폼을 갖는다는 것인데... 사실 이것은 이미 우리가 앞의 예제에서 음의지수쪽도 1/z = w 로 치환해서 테일러 급수를 얻었던 아이디어를 생각해보면, 매우 그럴싸한 것이다.
증명은, 우선 원점이 중심일때를 하고, 그리고 나서 중심을 이동시키기로 하자.
우선 중심이 원점인 도넛영역에서 f 가 어낼러틱 하다고 하자. 안쪽 반지름을 r , 바깥쪽 반지름을 R 이라고 하자. positively oriented 된 두개의 컨투어를 각각 Cr , CR 이라고 하자.
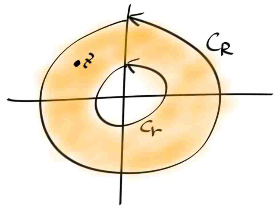도메인내에 임의의 점 z 에 대해, z를 둘러싸는 아주아주 작은 원 cρ 를 잡고, 다음과 같이 컨투어를 deform 하자.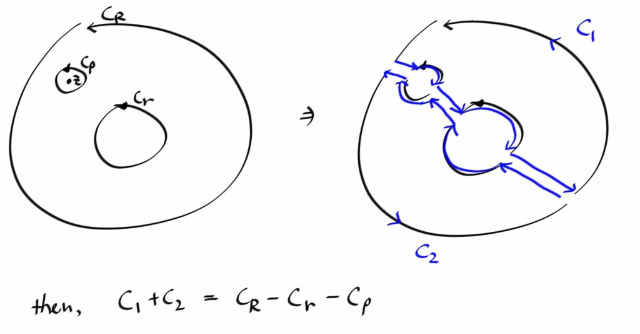 
그러면, 변수를 w 라고 하면, f(w) 는 C1 과 C2 내부에서 어낼러틱하고, C1 , C2 의 내부영역이 z 를 포함하지 않으므로, f(w) / ( w - z ) 는 C1 , C2 내부에서 어낼러틱 하다. 따라서 Cauchy-Goursat theorem 에 의해 아래와 같이 된다.
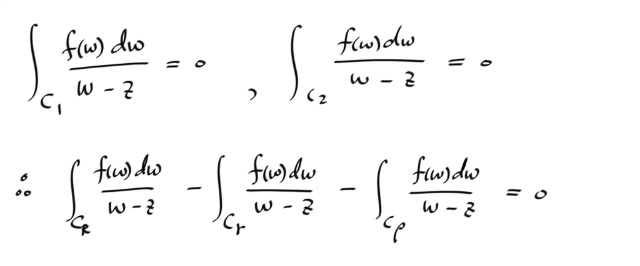
특히, 세번째 적분은 코시 인테그랄 포뮬러를 쓰면...
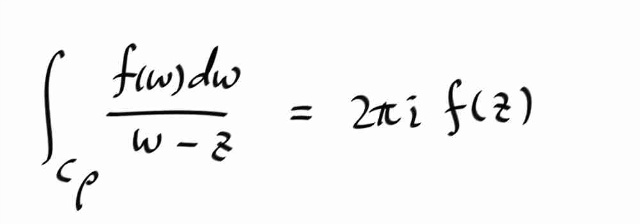가 되므로... f(z) 는 다음과 같이 쓸 수 있다.
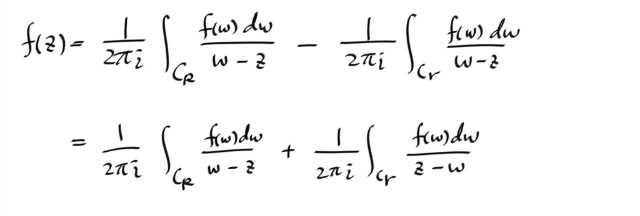
이제 테일러때 했던것 처럼, 1/(w-z) 와 1/(z-w) 를 시리즈로 전개하자.
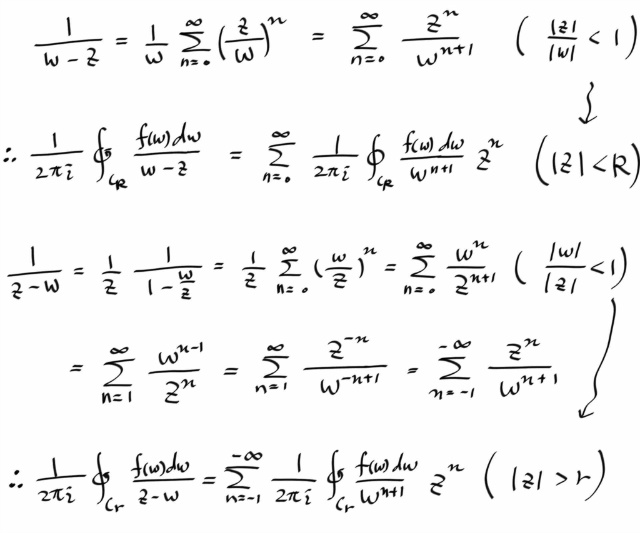
그런데, f(w) / w^(n+1) 은 Cr 과 CR 사이의 영역에서 어낼러틱 하므로, principle of deformation 에 의해서 그것의 Cr 에 대한 적분이나 CR 에 대한 적분이나 같다. 마찬가지로 Cr 과 CR 사이에 있는 임의의 positive oriented simple closed contour C 에 대해서도 같다.
따라서...
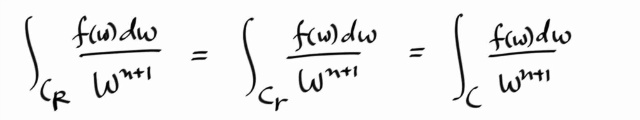
그리고, 적분변수 w 는 dummy 이므로 그냥 z로 써도 상관없다. 결과적으로 두파트의 써메이션을 한번에 쓸수 있고, f(z) 는 다음과 같이 된다.
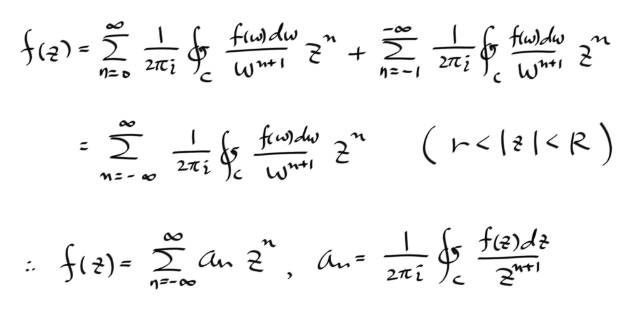
이제, 중심을 원점에서 z0 로 이동시키면, 최종적으로 원하는 식이 얻어진다.
-----------------------------------------------------------------------------------------------------
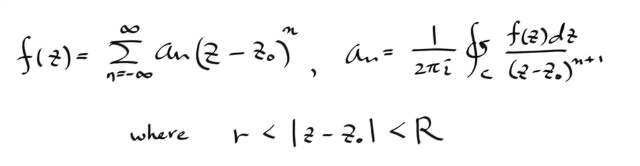
예제로 exp ( 1/z ) 의 시리즈 레프리젠테이션을 구해보자. 이경우는 exp z 를 알고있으므로, 간단하게 로렌트 시리즈를 구할 수 있다.
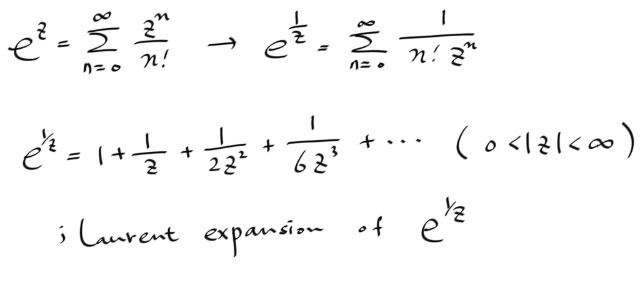
보통, 테일러 정리 증명은 시리즈의 파샬섬과 함수사이의 차이가 0 으로 다가간다는 것을 보이는 데, 우리는 그러한 엄밀한 방법 말고, 느낌만 얻을수 있는 스토리로 가자.
f(z) 가 중심이 원점이고, 반경 R 인 반시계방향으로 도는 컨투어 위와 안쪽에서 어낼러틱하다고 하자. 그러면 임의의 내부점 z 에 대해서 f(z) 는 코시 인테그랄 포뮬러에 의해 다음과 같이 쓸 수 있다.
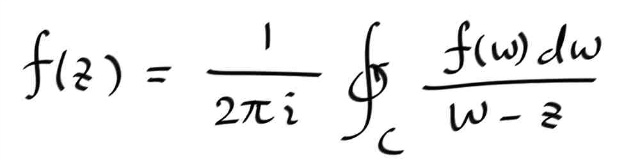
이때 피적분식에서 1 / ( w-z ) 를 기하급수로 전개하자.
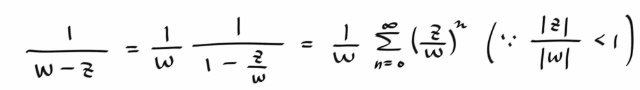
w 는 C 위에 있고, z 는 안쪽에 있으므로 수렴조건을 만족한다.
이제 서메이션 기호를 적분식 밖으로 빼자. 이때 요구되는 조건은 유니폼 컨버전스인데, 해석때 얘기하기로 하고, 된다고 치고 그냥 빼자.
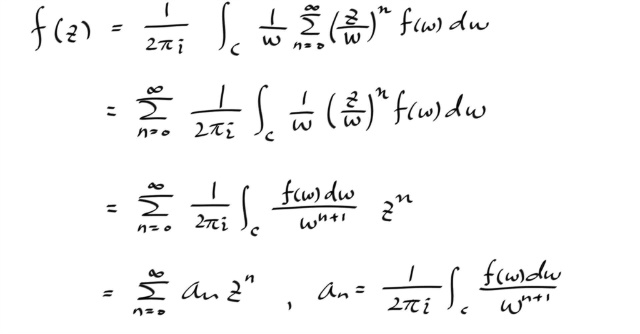
그런데, 계수 an 을 나타내는 적분식의 w 는 어차피 dummy variable 이므로, 아래와 같이 써도 된다.
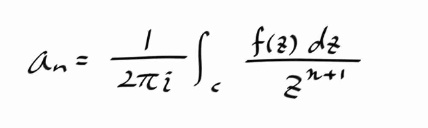
참고로 중심을 z0 로 쉬프트 시키고, 코시 적분공식을 쓰면, 원하는 결과를 얻는다.
----------------------------------------------------------------------------------------------------
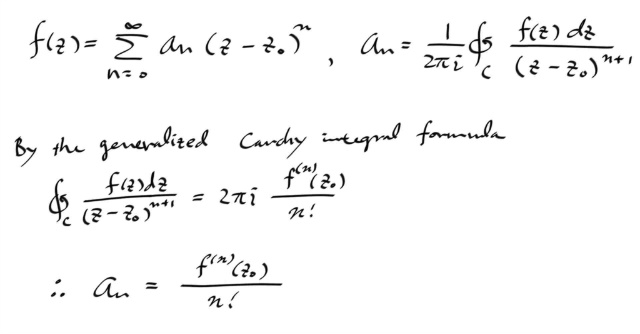
이제 로렌트 급수를 볼 차례이다.
미적시간의 기억을 되살려보자. 테일러 급수가 중심이 0 일때를 특히 맥로린 급수라고 했는데, 문제는 1/x 는 맥로린 급수로 전개할 수가 없다는 것이다. 1/x^2 도 마찬가지고, 1/x^3 도 마찬가지다. 즉, 저런녀석들은 0 에서 어낼러틱 하지 않다.
그러면, 임의의 함수를 1/x , 1/x^2 , 1/x^3 , ... 쪽으로도 전개하는 건 어떨까?
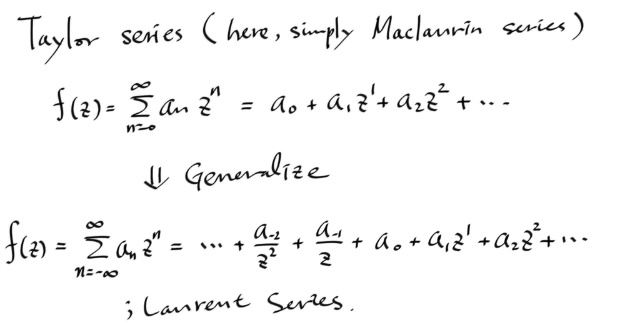
마찬가지로, 중심을 z0 로 쉬프트 시키면...
이제 할일은 계수를 계산하는 일 ( with 어떤 조건하에서... ) 이다.
로렌트 시리즈는 테일러 시리즈의 일반화로 생각될수 있으므로, 테일러 시리즈는 로렌트 시리즈에서 음수차수를 갖는 항들의 계수가 모두 0 인 특별한 케이스라고 말할 수 있다.
로렌트 시리즈에 대한 감을 얻기 위해, 직접 예를 하나 살펴보자.
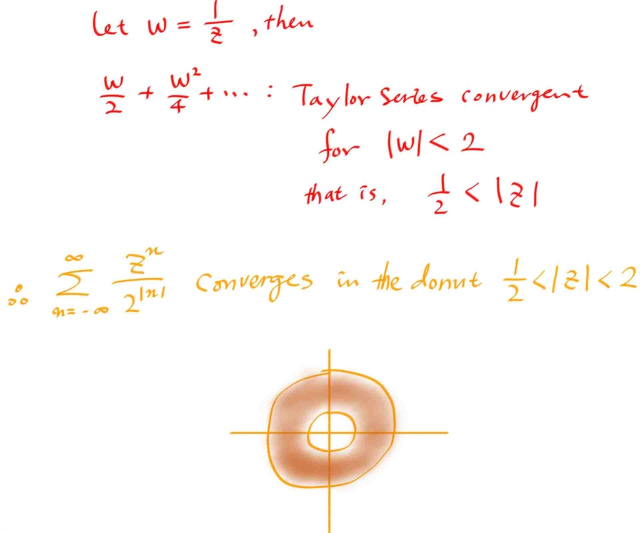
결과적으로, 로렌트 시리즈를 두 파트로 나누면, 양수 지수쪽은 반경 R 안쪽에서 수렴하는 테일러 급수고, 음수 지수쪽은 1/z = w 로 치환하면 역시 테일러급수이고, w가 반경 r 안쪽에서 수렴하는데, 다시 환원시키면 z 가 반경 r 바깥쪽에서 수렴하게 되어, 결국 위와같은 도넛모양의 수렴영역이 나오게 된다.
중심을 z0 로 이동시키면, 로렌트시리즈의 수렴영역은 보통 r < | z - z0 | < R 꼴이고, R 이 무한대 일수도 있고, r 이 0 일수도 있다. 물론 r=R 이 되어버린다던가 하면 테일러때도 그랬던 것처럼 수렴영역이 없어져버린다. 그리고, r = 0 인 경우, 수렴영역은 punctured disk 이다.
아무튼, 그래서 로렌트 시리즈는 다음과 같다.
일단 이것이 테일러 급수를 포함하는 개념인지 확인해보기 위해, 테일러급수의 상황, 즉, f 가 반경 R 안쪽에서 어낼러틱하다고 해보자. 즉 내부에 싱귤러 포인트가 없는경우다.
그러면, 음수지수에 대한 계수의 피적분식은 n=-k ( k ≥ 1 ) 라고 하면, f(z) / (z-z0)^(-k+1) 가 되고, 이것은 f(z) (z-z0)^(k-1) 이므로, 이 자체가 z0 에서도 어탤러틱하다. 따라서, 코시-구르사 정리에 의해 적분값은 0 이 된다. 즉, 음수 지수에 대한 계수들이 모두 0 이 되고, 곧 테일러 급수가 된다.
Note. 여기서 zo 는 도넛, 즉, 원의 중심이다. 그런데 f 는 도넛내부에서만 어낼러틱하면 되고, 도넛의 가운데 구멍영역에서는 어낼러틱하지 않아도 되는 상황이다. 그런데 z0 는 도넛의 중심이므로 도넛의 안쪽 구멍에 위치한다. 전개되는 항들을 보면 (z-z0) 의 음수지수들은 모두 z0 에서 어낼러틱하지 않다. 결국, 음수지수들은 z0 에 대해 어낼러틱하지 않은 텀들로 전개하고 있는것이다. 즉, 0에서 어낼러틱하지 않은 함수를 0 을 중심으로 전개할때, 중심에서 어낼러틱하지 않는 1/z , 1/z^2 , ... 들로 전개하는 것이다. (물론 양수지수 텀들에 추가적으로 ... )
아무튼 위의 정리가 사실이라면, 신기하게도 음수지수에 대한 계수도 양수지수에 대한 계수와 형식적으로 같은 폼을 갖는다는 것인데... 사실 이것은 이미 우리가 앞의 예제에서 음의지수쪽도 1/z = w 로 치환해서 테일러 급수를 얻었던 아이디어를 생각해보면, 매우 그럴싸한 것이다.
증명은, 우선 원점이 중심일때를 하고, 그리고 나서 중심을 이동시키기로 하자.
우선 중심이 원점인 도넛영역에서 f 가 어낼러틱 하다고 하자. 안쪽 반지름을 r , 바깥쪽 반지름을 R 이라고 하자. positively oriented 된 두개의 컨투어를 각각 Cr , CR 이라고 하자.
그러면, 변수를 w 라고 하면, f(w) 는 C1 과 C2 내부에서 어낼러틱하고, C1 , C2 의 내부영역이 z 를 포함하지 않으므로, f(w) / ( w - z ) 는 C1 , C2 내부에서 어낼러틱 하다. 따라서 Cauchy-Goursat theorem 에 의해 아래와 같이 된다.
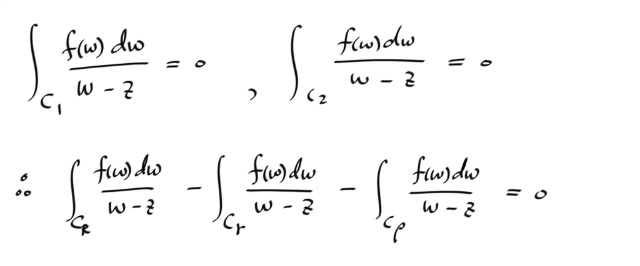
특히, 세번째 적분은 코시 인테그랄 포뮬러를 쓰면...
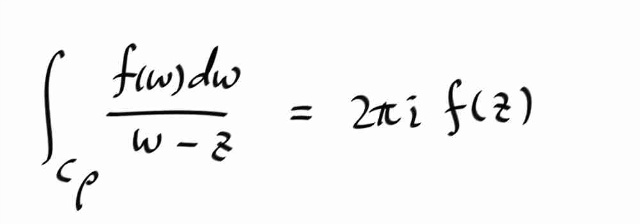
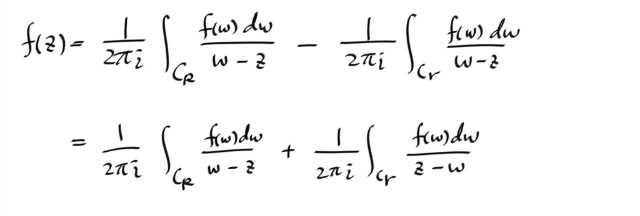
이제 테일러때 했던것 처럼, 1/(w-z) 와 1/(z-w) 를 시리즈로 전개하자.
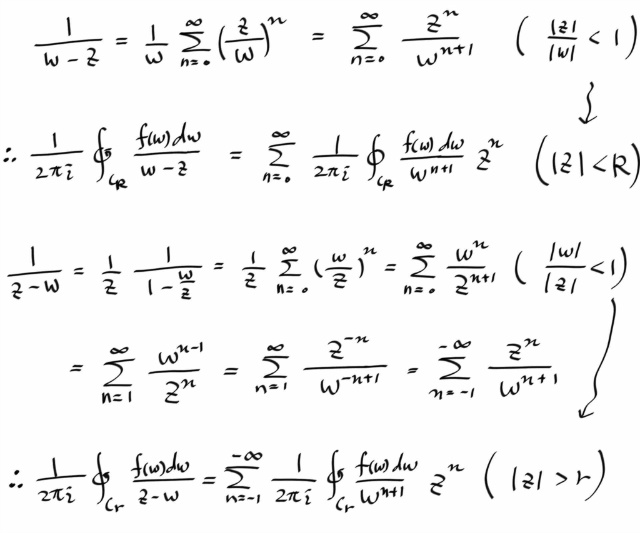
그런데, f(w) / w^(n+1) 은 Cr 과 CR 사이의 영역에서 어낼러틱 하므로, principle of deformation 에 의해서 그것의 Cr 에 대한 적분이나 CR 에 대한 적분이나 같다. 마찬가지로 Cr 과 CR 사이에 있는 임의의 positive oriented simple closed contour C 에 대해서도 같다.
따라서...
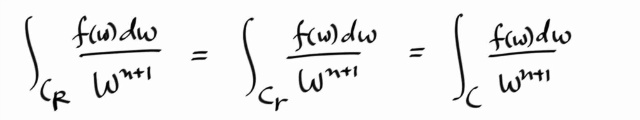
그리고, 적분변수 w 는 dummy 이므로 그냥 z로 써도 상관없다. 결과적으로 두파트의 써메이션을 한번에 쓸수 있고, f(z) 는 다음과 같이 된다.
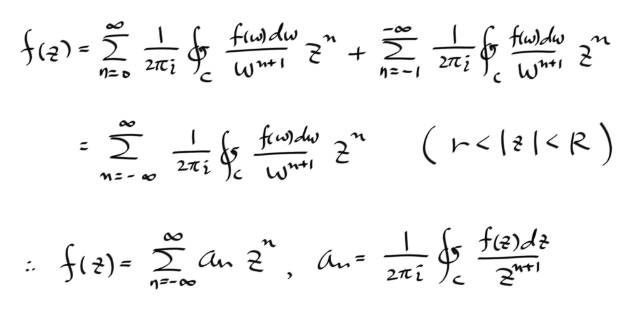
이제, 중심을 원점에서 z0 로 이동시키면, 최종적으로 원하는 식이 얻어진다.
-----------------------------------------------------------------------------------------------------
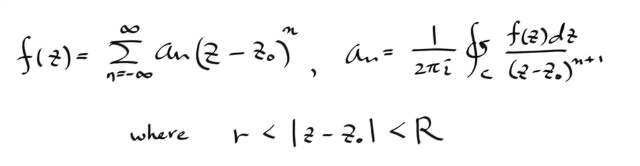
예제로 exp ( 1/z ) 의 시리즈 레프리젠테이션을 구해보자. 이경우는 exp z 를 알고있으므로, 간단하게 로렌트 시리즈를 구할 수 있다.