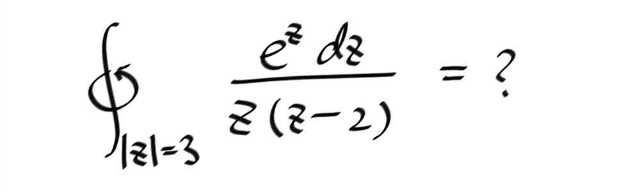Cauchy Integral Formula ( 코시 적분공식 )
Math/Complex2009. 7. 25. 02:22 |C 가 어떤 simple closed contour in the positive sense 라고 하고, f 는 C 위 & 내부에서 어낼러틱 하다고 하자.
그러면, C 의 내부에 있는 모든점 w 에 대해 다음이 성립하고, Cauchy Integral Formula 라고 부른다.
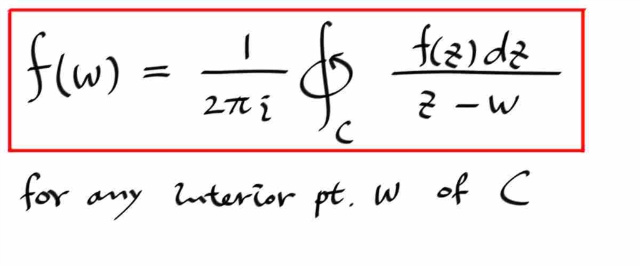
이때, f 는 C 안쪽에서 어낼러틱하지만, 1/(z-w) 가 곱해졌으므로, 내부영역의 어떠한 w 도, f(z) / (z-w) 에 대한 singluar point 임에 유의하자. 그렇지 않다면 코시-구르사 정리에 의해 적분값은 0 이 될 것이다.
특히, 피적분함수 f/(z-w) 가, 컨투어의 내부에서 싱귤러 포인트를 오직 하나 w 만 가지고 있음에 유의한다.
아무튼, 증명은 다음을 보이는 것으로 진행된다.
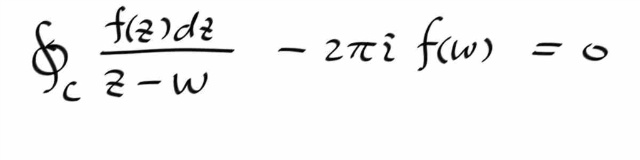
증명의 스케치는 이러하다. 우선 f(z) / (z - w ) 가 고려영역에서 w점을 빼고는 어낼러틱하다. 따라서, w 점을 감싸는 positive 방향으로 아주 작은 원으로 contour를 잡으면, 코시-구르사 정리와 path deformation 하면 C 에대한 적분이나 그 작은 원에대한 적분이나 같다.
또 f(w) / (z-w) 을 z로 적분할때 f(w) 가 밖으로 빠져나오고 2π i 가 되어 윗식의 두번째 항이 된다.
결국, 위에서 0 임을 보이고자 하는 좌변은 그 작은 원에 대해서 ( f(z) - f(w) ) / ( z - w ) 을 dz 로 적분한것과 같다. 즉, 이적분이 0 임을 보이면 된다. 적분에서의 삼각부등식과 입실론-델타를 써서, w를 감싸는 그 작은원을 작게만들어 이 적분값을 임의로 작게 만들수 있음을 보인다. 결과적으로 윗식을 증명한다.
코시 인테그랄 포뮬러는 변환관계로 볼수도 있는데, 아무튼 w 로 표시한 C 의 내부점을 변수로 볼 수 있으므로, w로 양변을 미분하면, 우변에서는 w로 미분하는것이 우변에서는 d/dw 가 적분식 안으로 들어갈수 있고, 몇 번 적용해보면 간단히 다음을 보일수 있다.
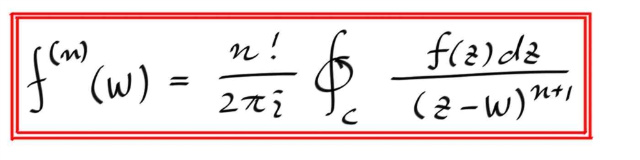
이식은 코시 적분 공식 자체를 포함하므로, Generalized Cauchy Integral Formula 라고 부르기도 한다. 당근 이거 하나만 기억하는게 더 경제적이다. 또한 위 식으로 부터, f 가 한번 복소미분 가능하면 ( holomorphic ) , 무한번 미분가능하다는 것을 확인할 수 있다. 즉, 복소해석에서 왜 holomorphic 을 analytic 과 혼용해서 쓰는지를 말해준다. 복소에서는 한번 미분가능하면, 자동으로 무한번 미분가능해서 taylor 전개가 가능하다.
제너럴라이즈드 코시 인테그랄 포뮬러를 이용해 적분을 계산하는 예제를 풀어보자.
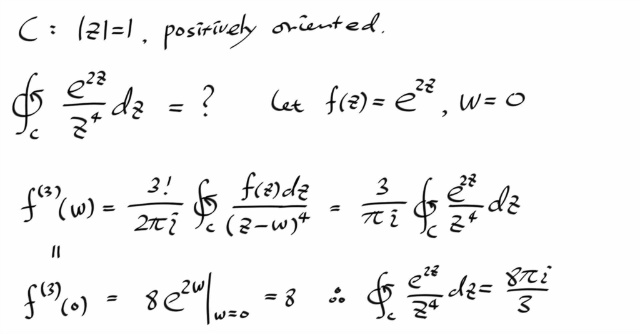
--------------------------------------------------------------------------------------------------
그럼, 여기서 퀴즈~
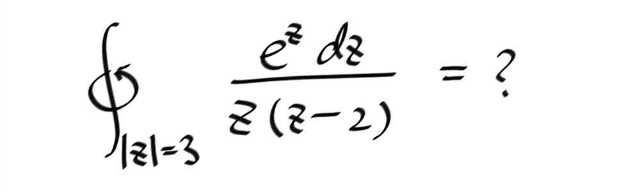
그러면, C 의 내부에 있는 모든점 w 에 대해 다음이 성립하고, Cauchy Integral Formula 라고 부른다.
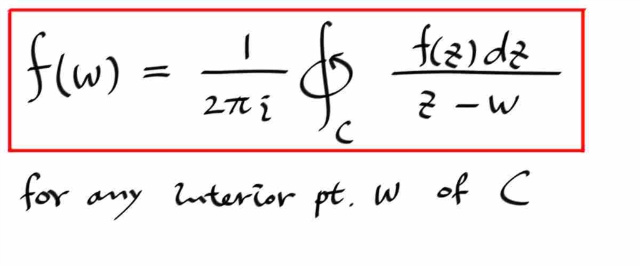
이때, f 는 C 안쪽에서 어낼러틱하지만, 1/(z-w) 가 곱해졌으므로, 내부영역의 어떠한 w 도, f(z) / (z-w) 에 대한 singluar point 임에 유의하자. 그렇지 않다면 코시-구르사 정리에 의해 적분값은 0 이 될 것이다.
특히, 피적분함수 f/(z-w) 가, 컨투어의 내부에서 싱귤러 포인트를 오직 하나 w 만 가지고 있음에 유의한다.
아무튼, 증명은 다음을 보이는 것으로 진행된다.
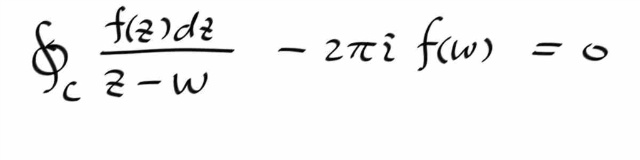
증명의 스케치는 이러하다. 우선 f(z) / (z - w ) 가 고려영역에서 w점을 빼고는 어낼러틱하다. 따라서, w 점을 감싸는 positive 방향으로 아주 작은 원으로 contour를 잡으면, 코시-구르사 정리와 path deformation 하면 C 에대한 적분이나 그 작은 원에대한 적분이나 같다.
또 f(w) / (z-w) 을 z로 적분할때 f(w) 가 밖으로 빠져나오고 2π i 가 되어 윗식의 두번째 항이 된다.
결국, 위에서 0 임을 보이고자 하는 좌변은 그 작은 원에 대해서 ( f(z) - f(w) ) / ( z - w ) 을 dz 로 적분한것과 같다. 즉, 이적분이 0 임을 보이면 된다. 적분에서의 삼각부등식과 입실론-델타를 써서, w를 감싸는 그 작은원을 작게만들어 이 적분값을 임의로 작게 만들수 있음을 보인다. 결과적으로 윗식을 증명한다.
코시 인테그랄 포뮬러는 변환관계로 볼수도 있는데, 아무튼 w 로 표시한 C 의 내부점을 변수로 볼 수 있으므로, w로 양변을 미분하면, 우변에서는 w로 미분하는것이 우변에서는 d/dw 가 적분식 안으로 들어갈수 있고, 몇 번 적용해보면 간단히 다음을 보일수 있다.
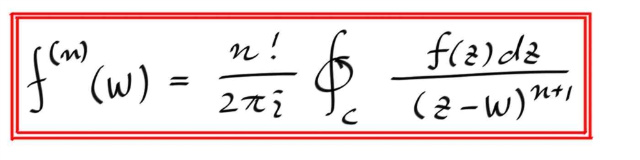
이식은 코시 적분 공식 자체를 포함하므로, Generalized Cauchy Integral Formula 라고 부르기도 한다. 당근 이거 하나만 기억하는게 더 경제적이다. 또한 위 식으로 부터, f 가 한번 복소미분 가능하면 ( holomorphic ) , 무한번 미분가능하다는 것을 확인할 수 있다. 즉, 복소해석에서 왜 holomorphic 을 analytic 과 혼용해서 쓰는지를 말해준다. 복소에서는 한번 미분가능하면, 자동으로 무한번 미분가능해서 taylor 전개가 가능하다.
제너럴라이즈드 코시 인테그랄 포뮬러를 이용해 적분을 계산하는 예제를 풀어보자.
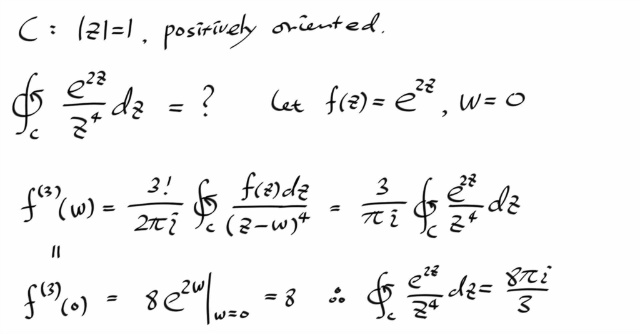
--------------------------------------------------------------------------------------------------
그럼, 여기서 퀴즈~