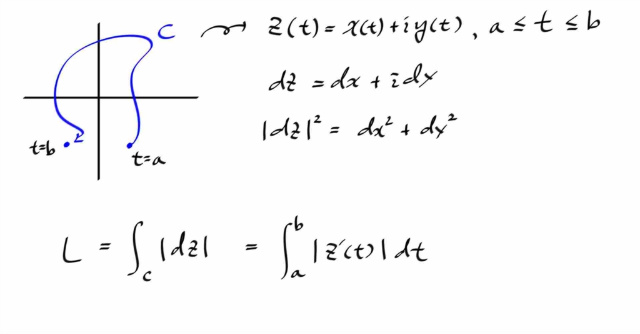Contour Integral

복소변수함수를 왜 하는가 에 대한 실용주의적 대답은 적분을 위해서? 라고 해도 과언이 아닐정도로, 복소함수의 이론은 적분에 있어서 강력한 도구를 제공한다. 그것이 진정 강력한 이유는 복소수가 전혀 등장하지 않는 실적분의 문제를 해결하는데 획기적인 방법을 제시한다는데에 있다.

가령, 아래와 같이 간단해 보이는 적분도, 실적분 테크닉만 가지고 풀어보면 드럽게 어렵다. ( 한번 도전해보는 것도 좋다. )

앞으로 메인으로 다루게 될 테마는 칸투어(contour) 인테그레이션과 레지두(residue) 캘큘러스이다.

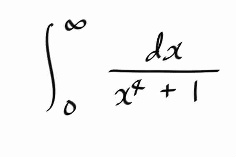
그전에, 전혀 새로울게 없지만 complex-valued 의 적분부터 시작하는게 순서다.


Complex Variable Functions 가 복소수에서 복소수로 가는 함수임에 반해, Complex-valued Functions 은 실수에서 복소수로 가는 함수이다.


예를들어   f( t )  =   2 t   +   i t ²     같은 함수가 complex-valued 펑션이다.  변수가 실수이므로, 당연히 적분변수는 실변수이다. 이러한 적분은 실적분과 다를게 없다. 그냥 각 성분함수를 따로 실변수 t 로 적분해주면 된다.


complex-valued 펑션의 적분 ( 사실상 두개의 실적분 ) 은 어떠한 이견도 있을수 없기 때문에, 복소적분상황에서 애매한 경우에 어떠한 매개변수에 의해 위와같은 상황이 연출되었다면, 그것은 가장 기초적이고 신뢰할수있는 답임은 확실하다.


이제  복소변수함수의 contour 적분을 시작해보자.

실적분의 상하한은 실수축상에서의 적분경로라고 볼수 있는데, 복소적분에서는 2차원이므로 적분상한과 적분하한으로 표현하는데 애로사항이 있다.

실적분에서 적분상하한으로 1차원적인 적분경로를 주었듯이, 복소적분에서는 2차원상에서의 적분경로를 주는데 그것을 contour 라고 한다. 그니까 벡터 캘큘에서 선 적분하는거랑 같은개념이다. 보통, 실매개변수에 의해 표현되어 complex-valued 가 된다.


요컨대, 컨투어 인테그랄은 실적분으로 치자면 정적분과 같은 것이다.


더 나아가, 실적분에서 미적분학의 기본정리 ( FTC , fundamental theorem of calculus ) 가 역도함수(Anti-derivative) 와 정적분(definite integration) 을 연결해준것 같이, 복소적분에서도 FTC 가 있고, 그것은 컨투어 인테그랄과 역도함수를 연결해준다. 즉, 피적분함수의 역도함수를 구해서 적분을 간단히 계산하는 방법도 있는데, 이것은 나중에 살펴볼 것이다. Anti-derivative 입장에서 보자면, 그것은 analytic 한것이고, 복소에서 analytic 이면 자동으로 harmonic 이고, 그에 따라 유용한 정리들이 쏟아져나오는데, 나중에 살펴볼 것이다.


아무튼, 실매개변수를 통한 contour 인테그랄은 간단히 말해, contour 를 나타낼때 사용된 실변수로 좨다나타내서 그 변수로 complex-valued 적분하는 것이다.

이때 f 안에 들어가는 z 는 주어진 contour 에 의존하므로, 매개변수 t 에 의해 곧바로 나타내졌다. 만약 contour 가 서로 다른 두 곡선이 결합된 형태라고 하면, 경로를 두개로 찢어서 각각의 경로에서 f 에 들어가는 z 는 형태가 달라야 할것이다.
 


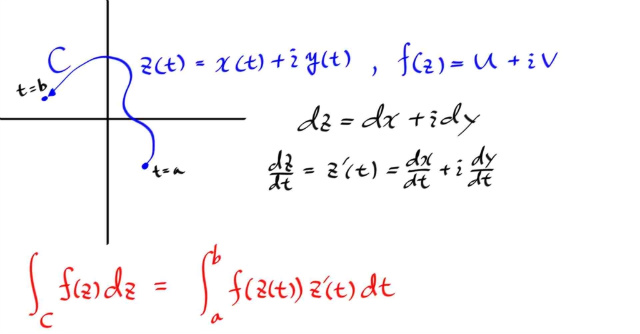
아무튼 예제를 풀어보자.

f 를  "인풋으로 들어온 복소수를 컴플렉스 컨주게이트해서 아웃풋으로 내놓는 함수" 라고 하자.
이 f 를, 중심이 원점인 반지름 2 인 반원 ( 각도는 -90도 에서 0 도를 거처 90 도에 이르는 , 즉, 4사분면에서 1사분면으로 진행되는... )  상에서 적분을 해보자.

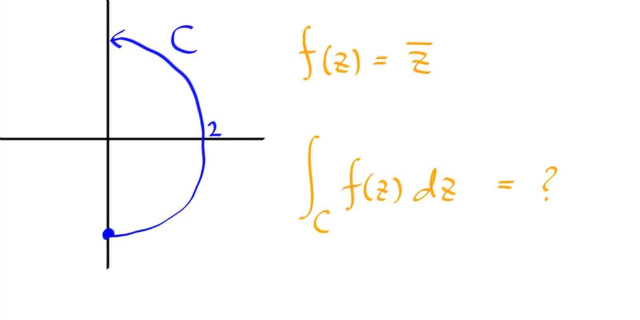
참고로, 주어진 함수 ( complex conjuate 를 취하는... ) 는 어낼러틱 하지 않다. 즉 미분이 안된다. 그럼에도 적분은 되는데, 이것은 실함수때와 마찬가지다.



아무튼, 적분경로는 매개변수를 t 라고 하면, z(t) = 2 exp ( i t )  with  -π/2 ≤ t ≤ π/2  로 나타낼수 있다. 따라서...

한문제 더 풀어보자.

주어진 복소수의 역수를 취하는 함수, 즉 f =  1/z 을 반지를 R 이고 반시계방향으로 회전하는 원 위에서 적분해보자.

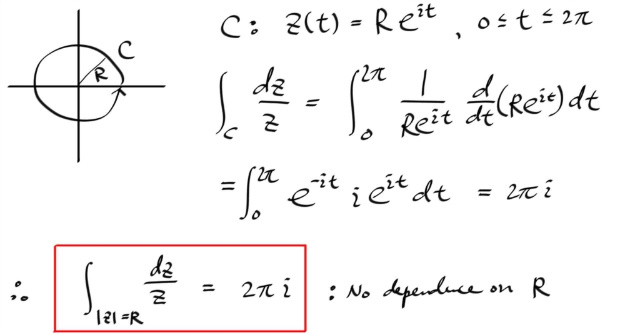
즉, 컨투어의 반지름에 상관없이, 중심이 원점인 원위에서의 1/z 을 적분하면 항상 2π i 가 된다.  ( 복소에서는 보통 별말이 없으면 컨투어를 CCW ( counterclockwise ) 방향으로 잡는 컨벤션이 있다. 만약 위의 적분을 반대방향 경로로 적분하면 적분값은 - 2 π i 가 된다. )


원의 중심을 옮기고, 피적분함수도 그만큼 shift 시켜서 직접 적분해보면 다음을 확인할 수 있다.

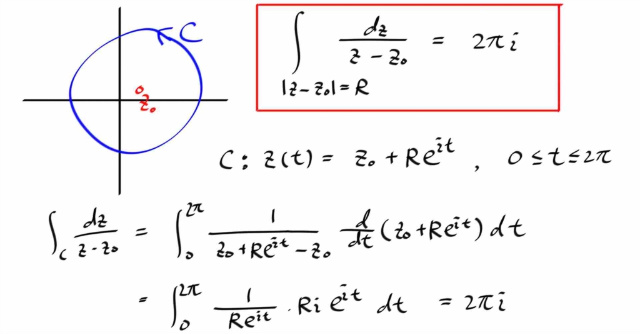
마지막으로, 컨투어의 arc length 는 다음과 같이 구하면 된다.