[복수변수함수] 초등함수(Elementary Functions)
Math/Complex2009. 7. 22. 00:56 |복소지수를 정의할때 이미 지수함수와 로그함수는 정의했으므로, 얘네들은 간단히 미분만 살펴보자.
어떤 멀티벨류드 로그펑션의 임의의 브랜치를 잡아서 싱글벨류드로 만들었다고 하고 미분을 해보자.
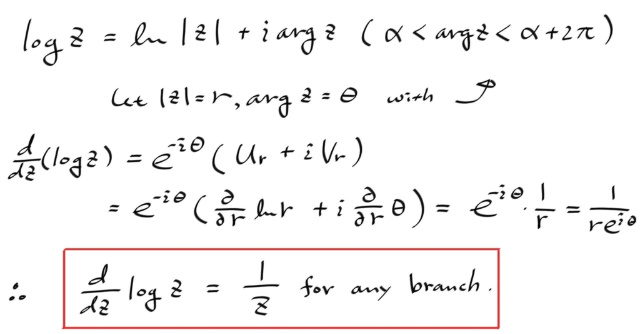
따라서 브랜치를 어떻게 선택하던간에, 실수때 하던것처럼 로그의 미분을 하면된다.
지수함수도 미분해보자.
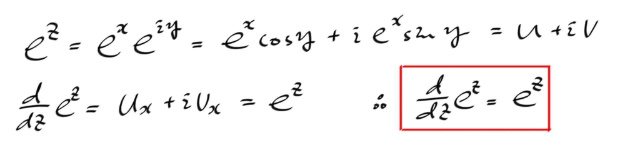
밑이 다른경우에, 밑을 e 로 바꾸고 지수에 로그를 올려서 정의했으므로, 그대로 하면되고, 해석때 합성함수의 미분을 임의의 메트릭 스페이스에서 증명했었으므로 그대로 쓰면 다음과 같이 된다. ( 메트릭 없이, 다른 방식으로 증명해도 마찬가지 )
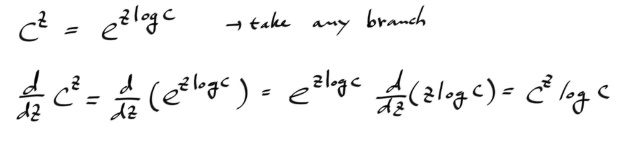
Power Rule 을 살펴보자.
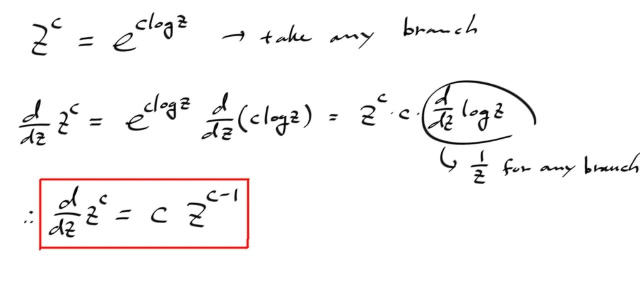 마지막 줄에, 지수 c 하고 지수 -1 을 지수법칙을 써서 붙여썼는데, 이것은 -1 이 정수이므로 가능하다.
마지막 줄에, 지수 c 하고 지수 -1 을 지수법칙을 써서 붙여썼는데, 이것은 -1 이 정수이므로 가능하다.
이제 삼각함수(trigonometric functions)하고 쌍곡선함수(hyperbolic functions)를 살펴보자.
삼각함수와 쌍곡선함수의 정의는 다음과 같다.
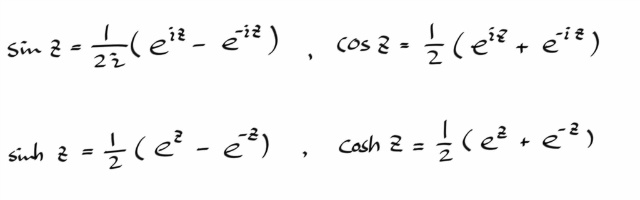
tan , tanh , sec , sech 따위도 모두 위의 정의를 사용해서 정의한다.
z 대신 iz 를 넣으면 바로 다음을 확인한다.
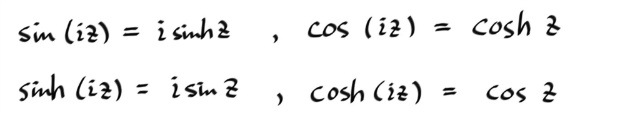
이상태에서 z 대신 iz 를 한번더 대입하면 다음을 확인한다.
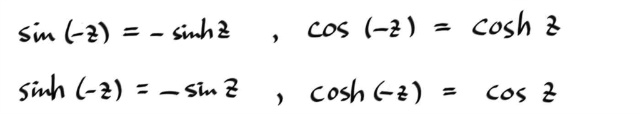
또한, cos ² z + sin ² z = 1 을 쉽게 확인할 수 있고, 역시 z대신 iz 대입하면 다음을 얻는다.
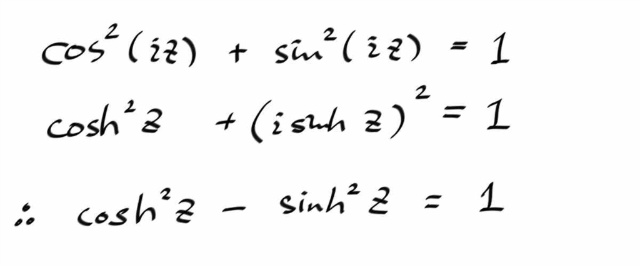
마찬가지로, sin ( z1 + z2 ) 와 cos ( z1 + z2 ) 공식을 유도할수 있고, z1 , z2 대신에 iz1 , iz2 를 대입하면 쌍곡선함수에 관한 공식을 얻을수 있다.
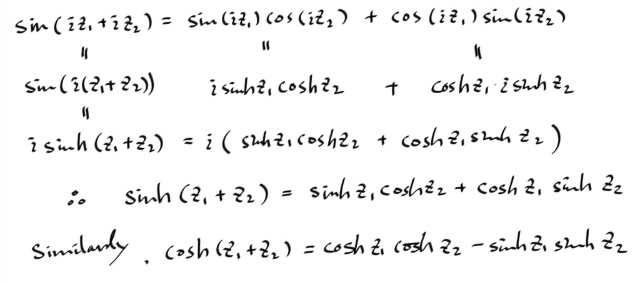
미분도 해보면 실수에서의 삼각함수때와 같은형태로 모두 성립한다.
어떤 멀티벨류드 로그펑션의 임의의 브랜치를 잡아서 싱글벨류드로 만들었다고 하고 미분을 해보자.
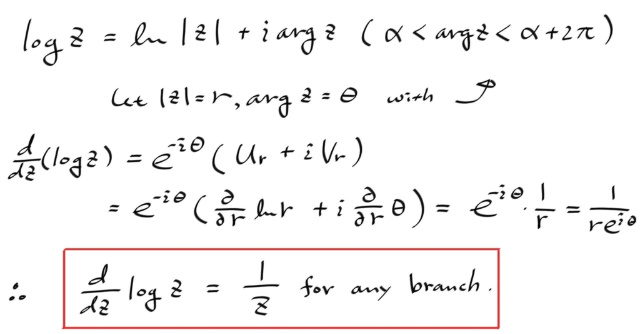
따라서 브랜치를 어떻게 선택하던간에, 실수때 하던것처럼 로그의 미분을 하면된다.
지수함수도 미분해보자.
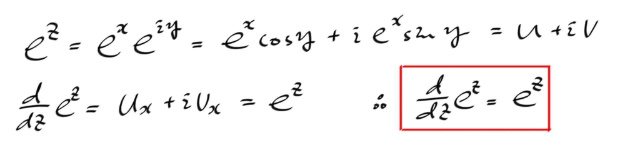
밑이 다른경우에, 밑을 e 로 바꾸고 지수에 로그를 올려서 정의했으므로, 그대로 하면되고, 해석때 합성함수의 미분을 임의의 메트릭 스페이스에서 증명했었으므로 그대로 쓰면 다음과 같이 된다. ( 메트릭 없이, 다른 방식으로 증명해도 마찬가지 )
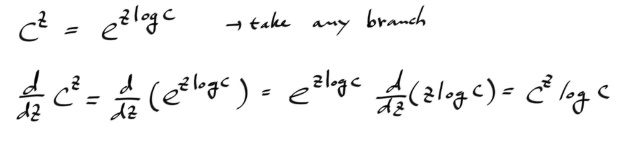
Power Rule 을 살펴보자.
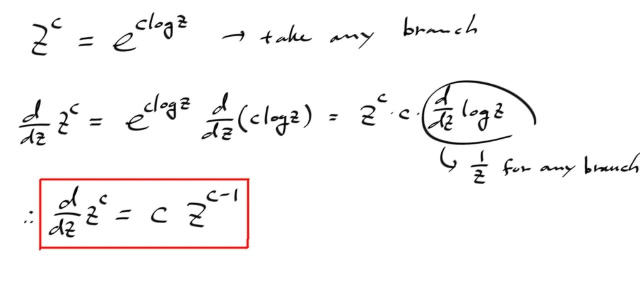
이제 삼각함수(trigonometric functions)하고 쌍곡선함수(hyperbolic functions)를 살펴보자.
삼각함수와 쌍곡선함수의 정의는 다음과 같다.
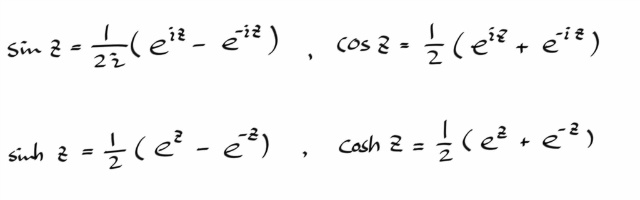
tan , tanh , sec , sech 따위도 모두 위의 정의를 사용해서 정의한다.
z 대신 iz 를 넣으면 바로 다음을 확인한다.
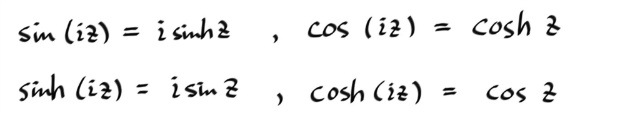
이상태에서 z 대신 iz 를 한번더 대입하면 다음을 확인한다.
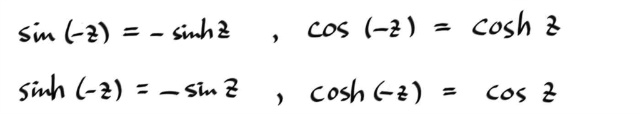
또한, cos ² z + sin ² z = 1 을 쉽게 확인할 수 있고, 역시 z대신 iz 대입하면 다음을 얻는다.
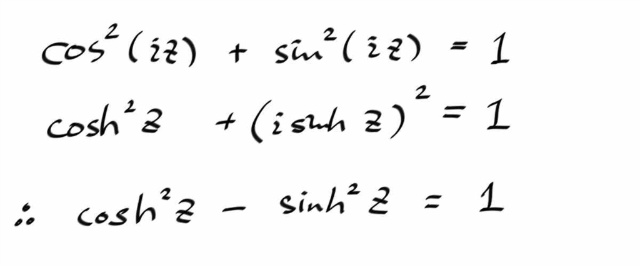
마찬가지로, sin ( z1 + z2 ) 와 cos ( z1 + z2 ) 공식을 유도할수 있고, z1 , z2 대신에 iz1 , iz2 를 대입하면 쌍곡선함수에 관한 공식을 얻을수 있다.
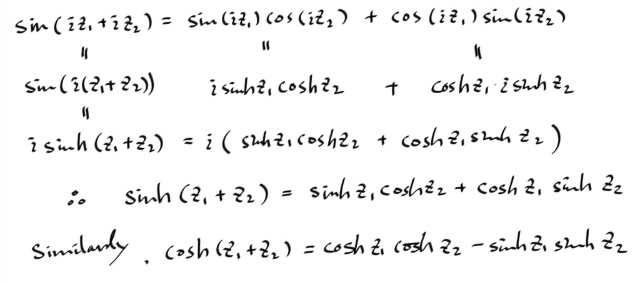
미분도 해보면 실수에서의 삼각함수때와 같은형태로 모두 성립한다.
