[중학수학] 산술평균과 기하평균

수열의 입장에서 보면 산술평균은 등차수열의 중간항으로 생각되어질 수 있다. 가령 1, 5, 9, 13, 17, 21, ... 처럼 4씩 증가하는 등차수열을 보면, 각 항은 자신의 바로앞뒤에 있는 두항의 산술평균이된다.


등차수열과 마찬가지로 기하순열(geometric sequence)의 각 항은 앞뒤항의 일종의 중간치로 볼 수 있는데, 이를 기하평균이라고 부른다. 가령 1, 3, 9, 27, 81, ...   처럼 3배씩 뛰는 기하순열에서 3을 1과 9의 기하평균이라고 부르고, 9를 3과 27의 기하평균이라고 부르는 식이다. 산술평균이 두값을 더해서 2로 나누는것과는 달리, 기하평균은 두값을 곱하고 루트를 씌우면 된다.

마찬가지로 등차순열을 분수꼴로 뒤집어서 조화수열(harmonic seq.) 이라는 것을 만들면, 위와 똑같은 컨셉으로 조화평균을 정의할 수 있다. 가령, 앞에서 예로든 등차수열, 1, 5, 9, 13, 17, 21 , ... 에 대응되는 조화수열은 1, 1/5, 1/9, 1/13, 1/17, 1/21 , ... 이 되는데, 이때 1/13 을 1/9 과 1/17 의 조화평균이라고 부른다.


산술평균과 기하평균을 작도의 관점에서 생각해보자.

두개의 서로다른 길이를 갖는 선분AB 와 선분 BC 를 생각하자. 두 선분을 나란히 붙히고, 중선을 긋고 원을 그리면, 쉽게 두 선분의 평균을 작도할 수 있다.

그림에서 선분 EF 는 선분 AB 와 BC 의 산술평균이다.

한편 기하평균은, B점에서 수선을 그어, 원과 만나는 길이가 된다.

위 그림에서 BG가 AB, BC 의 기하평균이 되는데, 이는 지름에 대한 원주각이 직각이되어, 삼각형 AGC 가 직각삼각형이 되고, 닮음관계를 이용하면, BG의 제곱이 AB x BC 가 됨으로 부터 확인할 수 있다.

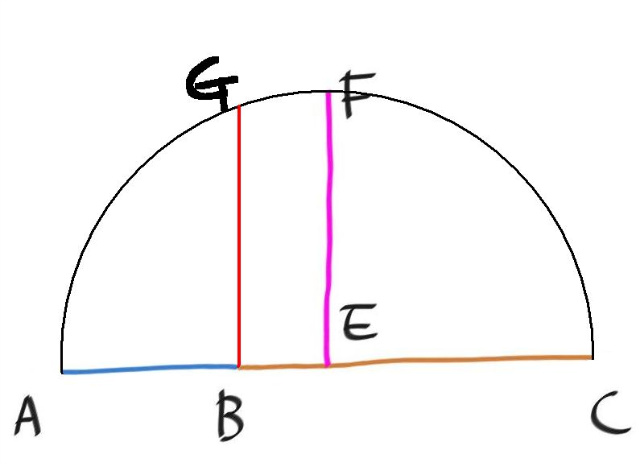
위의 그림에서 AB 의 길이를 줄이고 그만큼 BC 의 길이를 늘리면, 결과적으로 점B 의 위치만 이동하게 되는데, 그러한 이동에 대해서 산술평균 EF 는 변함이 없고, 기하평균 BG 만 변하게 된다.

그림으로 부터 "산술평균 ≥ 기하평균" 의 유용한 부등식을 확인하게 된다.