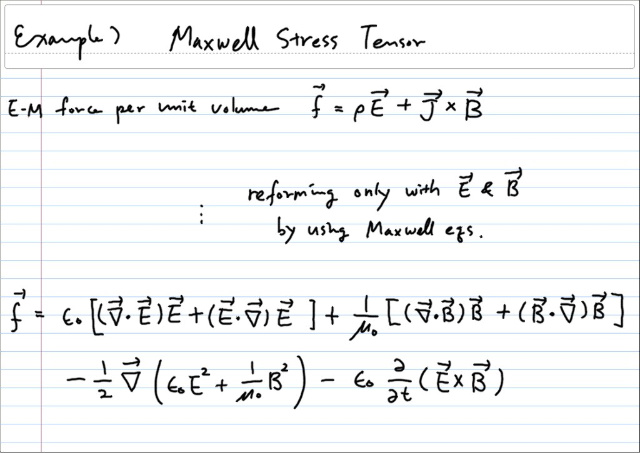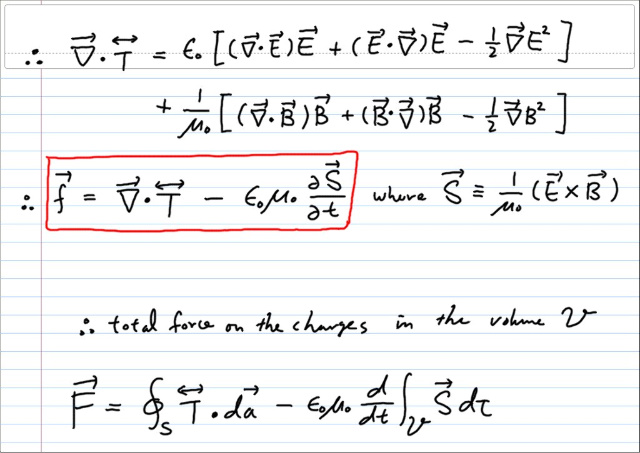다이애드 dyad
Physics/Math./Mech./Gen. Relativity2009. 3. 26. 00:57 |포스팅을 한지 좀 오래되었다. 내일도 양자숙제를 내야되는 관계로 이러고 있을 시간도 없고, 이래서도 안되지만... 오늘은 장시간 실험하느라 오존을 너무 먹어서 목도 좀 아픈 관계로... 쉬어야겠다.
꽤 오래전에 텐서이야기를 한창 좀 쓰다가, 진행이 너무 느려서, 말아버린적이 있는데... 이어서 한편 더 써볼까 한다.
텐서에 관한 앞의 글 몇개를 리뷰해보면...
1. 좌표계에 무관하게 물리법칙을 기술하기 위해서 텐서를 도입했다고 했고,
2. 베이시스와 결합해서 완결된 하나의 정보를 갖는다고 했다.
3. 필요한 성분의 수에 따라, 값, 열, 행렬 등으로 레프리젠트 할 수 있었고,
4. 특정한 변환 규칙을 만족해야 했다. ( 직교베이시스 변환에 관한 성분변환 규칙 )
5. 스케일러의 경우, 좌표변환에 완전하게 인베리언스 였고, 따라서 베이시스와 결합할 필요가 없었다.
( 어차피 성분도 하나뿐이라서 베이시스랑 결합도 못하지만... )
6. 벡터의 경우, 베이시스 벡터와 각 성분이 결합하여 하나의 완결된 물리적 벡터를 나타냈다.
7. 랭크 2 텐서의 경우 메이트릭스로 레프리젠트 할 수 있었다.
스케일러는 베이시스에 대응할 필요가 없었고, 벡터의 각 성분은 각각의 베이시스 벡터와 대응되었다. 그렇다면 메이트릭스로 레프리젠트된 랭크2 텐서의 각 성분은 무엇과 대응되는가? 라는 질문은 자연스럽다.
그것은 바로 dyad 이다. 이와 마찬가지로 랭크3 텐서는 triad , 뭐 이런식으로 나간다. 이게 뭐냐면 벡터를 그냥 나란히 쓴거다.
아니 벡터를 그냥 나란히 쓰다니, 그게 무슨 의미가 있는가 라고 되물을지도 모르겠다. 굳이 대답하자면 "정보" 랄까? 일단 dyad 에 대해서 간략히 알아보자.
가령 두벡터 a , b 가 있을때, 이 두벡터의 다이애드는 그냥 나란히 ab 라고 쓰면 된다. ( 사실은 이 자체도 텐서이다. )
이것은 어떠한 성질이 있는가, 가령 새로운 벡터 c 에 닷 프로덕트를 해보자. 일반적으로 닷 프로덕트는 커뮤트하는데, 이경우엔 그렇지가 않다. ab dot c = a ( b dot c ) , c dot ab = ( c dot a ) b 가 되어, 전자의 경우 a 방향을 갖고, 후자의 경우 b 방향을 갖는다. 즉, 다른 벡터이다.
또한, 이것은 c 라는 벡터에 오퍼레이트되어 전혀 다른 방향의 a 혹은 b 벡터 방향의 벡터로 바꿔놓았다. 전기장과 polarization 을 통해서 텐서를 구성했던 기억을 되살려보면, 상당히 텐서스럽다(?)는 생각이 들것이다.
자, 아무튼 다이애드 ab 는 두벡터 a와 b의 정보를 모두 포함한다. 오소노말 베이시스에 대해 성분분해를 해보고 어떻게 되는지 살펴보자. ( 아인슈타인 노테이션에 주의할 것 )
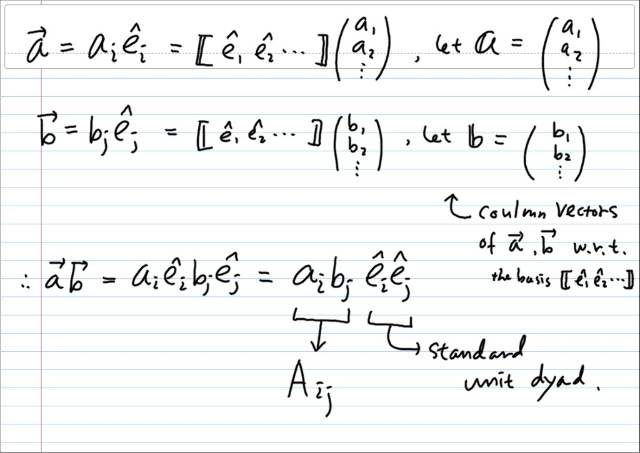
a_i b_j 에서 보듯이 다이애드는 사실상 첨자를 두개를 갖게되므로, 행렬 레프리젠테이션을 쓰면 자연스럽다. a_i b_j 를 i,j 성분으로 하는 메이트릭스를 잡으면, 다음과 같이 된다.

이것은 선형대수에서 컬럼벡터로 내적을 표현할때 a transpose b 했던것과 한끗차이지만 꽤 다르다. 우선 내적하면 벡터 (rank1) 두개가 컨트랙션 되어 rank 0 로 떨어지지만, dyadic product 를 하면, 두 rank 가 서로 더해진다. 즉, rank 1 + rank 1 = rank2 텐서로 올라간다.
많은경우 이렇게 곱하는 방식을 보통 "다이애딕 프로덕트" , "텐서 프로덕트" 따위로 부른다. 그리고 위와같은 곱하기에 똥골뱅이한 표시를 사용한다. 행렬로 보면, 열벡터와 행벡터의 "크로네커 프로덕트" 가 된다. ( 행렬의 곱은 많은 방식이 존재한다. 흔히 우리가 하는 보통의 행렬곱은 linear transformation 과 대응한다. )
동일한 베이시스에 대해 ( 즉, 베이시스를 고정하면, ) 모든 벡터는 그 베이시스에 대한 성분묶음과 1-1 대응이다. 즉, 같게 사용할 수 있다. 베이시스와 성분과의 관계는 수학적으로도 매우 중요한데, 일단은 그 두짝의 결합이 좌표변환에 대해 인베리언트 하다는 것만으로 충분하다.
나는 자꾸 "물리적 벡터" 혹은 "완결한 벡터" 라는 어색한 표현을 쓰고 있는데, 그것은 순전히 이러한 인베리언스를 나타내기위함이다. 가령, 두개의 듀얼 베이시스 ( 그러니까, 콘트라베리언트와 코베리언트 베이시스 , 둘 사이엔 리씨프로컬 관계가 있다 ) 를 잡는다면, 하나의 벡터는 각 베이시스와 그에대한 대응 성분과의 결합을 통해, 두개의 인베리언트한 묶음을 얻게 되는 것이다.
아무튼, 하나의 베이시스만 생각한다면, 벡터와 그것의 대응성분묶음 사이에는 1대1 대응하고, 결국, n-tuple 은 열벡터는 행벡터든 물리적 벡터와 동일하게 사용할수 있다. 즉, 그냥 수의 묶음을 "벡터" 라고 불러도 무방하다. ( 물론 텐서의 변환 규칙을 만족해야 하지만...)
그러나 우리의 마음속에는 이미 각 성분이 본래의 베이시스 벡터에 대응되고 있음을 알고 있다. 가령 어떤 벡터가 ( 2,3,4) 이다. 라고 한다면 2는 x축 방향, 3은 y축 방향, 4는 z축 방향으로 알아듣는 것이 그것이다.
마찬가지로, rank 2 의 텐서도 , 고정된 베이시스에 대해, 메이트릭스 레프리젠테이션과 "완결한" 텐서사이에 1대1 대응한다. 따라서, 그러한 메이트릭스를 텐서라고 불러도 무방하다. ( 물론, 텐서 변환 규칙을 만족하는 경우에 한해서이다. )
이때 각 성분에 대응되는 것이 (오소노말 베이시스에 대해) 바로 standard unit dyad 이다. ( standard 가 아닌 경우는 논외로 하자. )
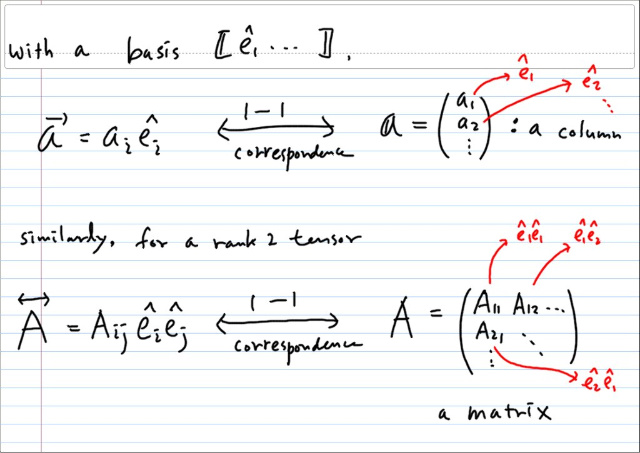
위에서 보듯이, 위에 화살표를 하는 것은 보통 물리적인 벡터를 나타내는 경우가 많고, 벡터 스페이스의 원소로서 쓸때는 겹소문자를 많이 쓰긴 하는데, 꼭 그런건 아니고, 특히, 볼드체로 쓸 경우엔 딱히 구분을 하지 않는 경우가 많다. ( 구분할 필요가 없거나, 문맥상 파악 가능하거나 등등... )
아무튼, 위에 화살표를 얹어서 물리적벡터 ( 즉, 베이시스 벡터들이 다 결합되어있는.. ) 로 표시하는 것처럼, 텐서도 그냥 메이트릭스 레프리젠테이션에 대해, 베이시스 다이애드들을 다 결합해놓은 완결한 상태에 보통 위에 쌍화살표를 쓰는 경우가 많다. 물론 항상 그런건 아니고, 단지 내가 선호하는 노테이션임을 밝혀둔다.
이제, 텐서와 벡터의 내적을 살펴보자.
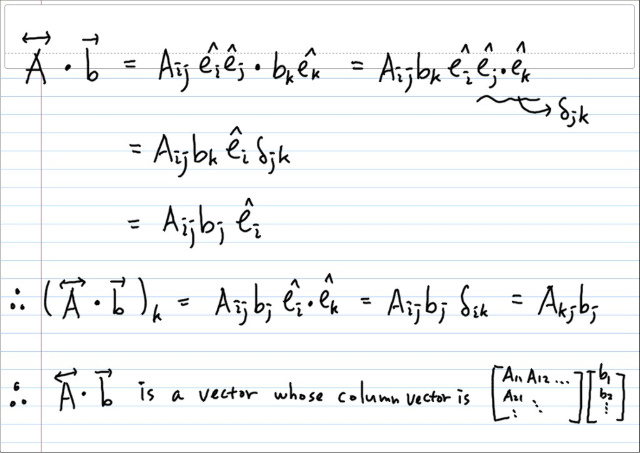
이경우에도 닷 프로덕트에 의해 랭크가 떨어지는 것을 확인 할 수 있다. 닷 프로덕트의 특징이다. 전체랭크합에 대해 두개씩 떨어뜨린다. 위의경우 A 가 2 , b 가 1 인데, 결과는 1 이다. 다이애드는 랭크를 올리고, 닷 프로덕트는 랭크를 떨어뜨린다.
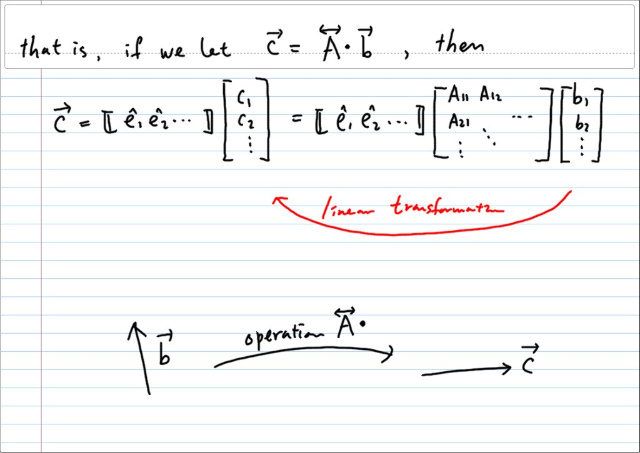
텐서와의 닷 프로덕트를, 벡터의 성분들만 가지고 살펴보면, 곧바로 일차변환임을 알 수 있다. 결국 공간상에서 벡터의 방향까지 변하게 할 수 있다. 그냥 스칼라를 곱했다면, 크기( 음수=반대방향 포함 )만을 바꿀수 있을 것이다.
글이 상당히 길어졌는데, 마지막으로, 전자기학의 맥스웰 스트레스 텐서에 dyad 가 어떻게 등장하는지 살펴보면서 끝맺도록 하겠다.
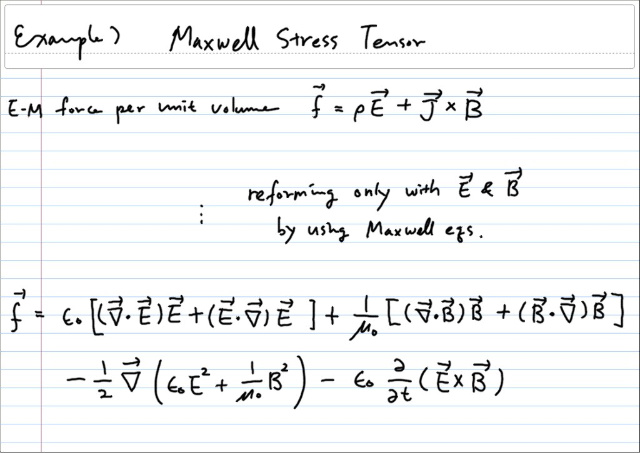

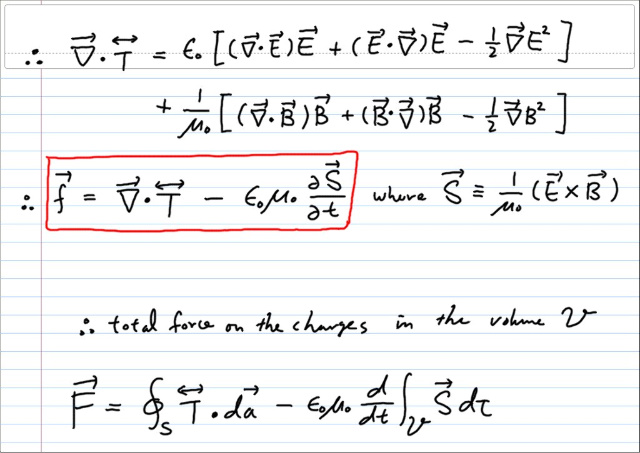
꽤 오래전에 텐서이야기를 한창 좀 쓰다가, 진행이 너무 느려서, 말아버린적이 있는데... 이어서 한편 더 써볼까 한다.
텐서에 관한 앞의 글 몇개를 리뷰해보면...
1. 좌표계에 무관하게 물리법칙을 기술하기 위해서 텐서를 도입했다고 했고,
2. 베이시스와 결합해서 완결된 하나의 정보를 갖는다고 했다.
3. 필요한 성분의 수에 따라, 값, 열, 행렬 등으로 레프리젠트 할 수 있었고,
4. 특정한 변환 규칙을 만족해야 했다. ( 직교베이시스 변환에 관한 성분변환 규칙 )
5. 스케일러의 경우, 좌표변환에 완전하게 인베리언스 였고, 따라서 베이시스와 결합할 필요가 없었다.
( 어차피 성분도 하나뿐이라서 베이시스랑 결합도 못하지만... )
6. 벡터의 경우, 베이시스 벡터와 각 성분이 결합하여 하나의 완결된 물리적 벡터를 나타냈다.
7. 랭크 2 텐서의 경우 메이트릭스로 레프리젠트 할 수 있었다.
스케일러는 베이시스에 대응할 필요가 없었고, 벡터의 각 성분은 각각의 베이시스 벡터와 대응되었다. 그렇다면 메이트릭스로 레프리젠트된 랭크2 텐서의 각 성분은 무엇과 대응되는가? 라는 질문은 자연스럽다.
그것은 바로 dyad 이다. 이와 마찬가지로 랭크3 텐서는 triad , 뭐 이런식으로 나간다. 이게 뭐냐면 벡터를 그냥 나란히 쓴거다.
아니 벡터를 그냥 나란히 쓰다니, 그게 무슨 의미가 있는가 라고 되물을지도 모르겠다. 굳이 대답하자면 "정보" 랄까? 일단 dyad 에 대해서 간략히 알아보자.
가령 두벡터 a , b 가 있을때, 이 두벡터의 다이애드는 그냥 나란히 ab 라고 쓰면 된다. ( 사실은 이 자체도 텐서이다. )
이것은 어떠한 성질이 있는가, 가령 새로운 벡터 c 에 닷 프로덕트를 해보자. 일반적으로 닷 프로덕트는 커뮤트하는데, 이경우엔 그렇지가 않다. ab dot c = a ( b dot c ) , c dot ab = ( c dot a ) b 가 되어, 전자의 경우 a 방향을 갖고, 후자의 경우 b 방향을 갖는다. 즉, 다른 벡터이다.
또한, 이것은 c 라는 벡터에 오퍼레이트되어 전혀 다른 방향의 a 혹은 b 벡터 방향의 벡터로 바꿔놓았다. 전기장과 polarization 을 통해서 텐서를 구성했던 기억을 되살려보면, 상당히 텐서스럽다(?)는 생각이 들것이다.
자, 아무튼 다이애드 ab 는 두벡터 a와 b의 정보를 모두 포함한다. 오소노말 베이시스에 대해 성분분해를 해보고 어떻게 되는지 살펴보자. ( 아인슈타인 노테이션에 주의할 것 )
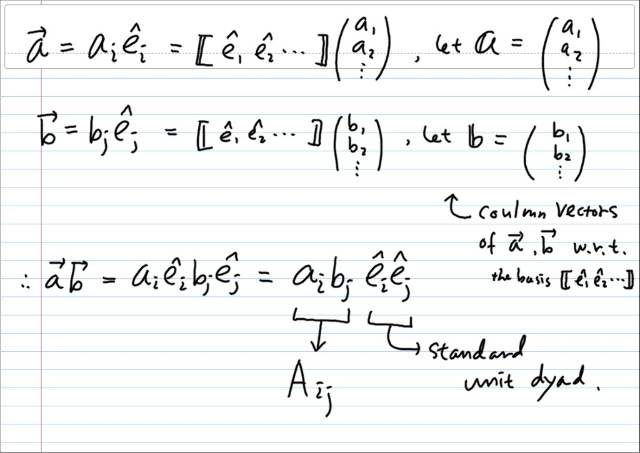
a_i b_j 에서 보듯이 다이애드는 사실상 첨자를 두개를 갖게되므로, 행렬 레프리젠테이션을 쓰면 자연스럽다. a_i b_j 를 i,j 성분으로 하는 메이트릭스를 잡으면, 다음과 같이 된다.

이것은 선형대수에서 컬럼벡터로 내적을 표현할때 a transpose b 했던것과 한끗차이지만 꽤 다르다. 우선 내적하면 벡터 (rank1) 두개가 컨트랙션 되어 rank 0 로 떨어지지만, dyadic product 를 하면, 두 rank 가 서로 더해진다. 즉, rank 1 + rank 1 = rank2 텐서로 올라간다.
많은경우 이렇게 곱하는 방식을 보통 "다이애딕 프로덕트" , "텐서 프로덕트" 따위로 부른다. 그리고 위와같은 곱하기에 똥골뱅이한 표시를 사용한다. 행렬로 보면, 열벡터와 행벡터의 "크로네커 프로덕트" 가 된다. ( 행렬의 곱은 많은 방식이 존재한다. 흔히 우리가 하는 보통의 행렬곱은 linear transformation 과 대응한다. )
동일한 베이시스에 대해 ( 즉, 베이시스를 고정하면, ) 모든 벡터는 그 베이시스에 대한 성분묶음과 1-1 대응이다. 즉, 같게 사용할 수 있다. 베이시스와 성분과의 관계는 수학적으로도 매우 중요한데, 일단은 그 두짝의 결합이 좌표변환에 대해 인베리언트 하다는 것만으로 충분하다.
나는 자꾸 "물리적 벡터" 혹은 "완결한 벡터" 라는 어색한 표현을 쓰고 있는데, 그것은 순전히 이러한 인베리언스를 나타내기위함이다. 가령, 두개의 듀얼 베이시스 ( 그러니까, 콘트라베리언트와 코베리언트 베이시스 , 둘 사이엔 리씨프로컬 관계가 있다 ) 를 잡는다면, 하나의 벡터는 각 베이시스와 그에대한 대응 성분과의 결합을 통해, 두개의 인베리언트한 묶음을 얻게 되는 것이다.
아무튼, 하나의 베이시스만 생각한다면, 벡터와 그것의 대응성분묶음 사이에는 1대1 대응하고, 결국, n-tuple 은 열벡터는 행벡터든 물리적 벡터와 동일하게 사용할수 있다. 즉, 그냥 수의 묶음을 "벡터" 라고 불러도 무방하다. ( 물론 텐서의 변환 규칙을 만족해야 하지만...)
그러나 우리의 마음속에는 이미 각 성분이 본래의 베이시스 벡터에 대응되고 있음을 알고 있다. 가령 어떤 벡터가 ( 2,3,4) 이다. 라고 한다면 2는 x축 방향, 3은 y축 방향, 4는 z축 방향으로 알아듣는 것이 그것이다.
마찬가지로, rank 2 의 텐서도 , 고정된 베이시스에 대해, 메이트릭스 레프리젠테이션과 "완결한" 텐서사이에 1대1 대응한다. 따라서, 그러한 메이트릭스를 텐서라고 불러도 무방하다. ( 물론, 텐서 변환 규칙을 만족하는 경우에 한해서이다. )
이때 각 성분에 대응되는 것이 (오소노말 베이시스에 대해) 바로 standard unit dyad 이다. ( standard 가 아닌 경우는 논외로 하자. )

위에서 보듯이, 위에 화살표를 하는 것은 보통 물리적인 벡터를 나타내는 경우가 많고, 벡터 스페이스의 원소로서 쓸때는 겹소문자를 많이 쓰긴 하는데, 꼭 그런건 아니고, 특히, 볼드체로 쓸 경우엔 딱히 구분을 하지 않는 경우가 많다. ( 구분할 필요가 없거나, 문맥상 파악 가능하거나 등등... )
아무튼, 위에 화살표를 얹어서 물리적벡터 ( 즉, 베이시스 벡터들이 다 결합되어있는.. ) 로 표시하는 것처럼, 텐서도 그냥 메이트릭스 레프리젠테이션에 대해, 베이시스 다이애드들을 다 결합해놓은 완결한 상태에 보통 위에 쌍화살표를 쓰는 경우가 많다. 물론 항상 그런건 아니고, 단지 내가 선호하는 노테이션임을 밝혀둔다.
이제, 텐서와 벡터의 내적을 살펴보자.
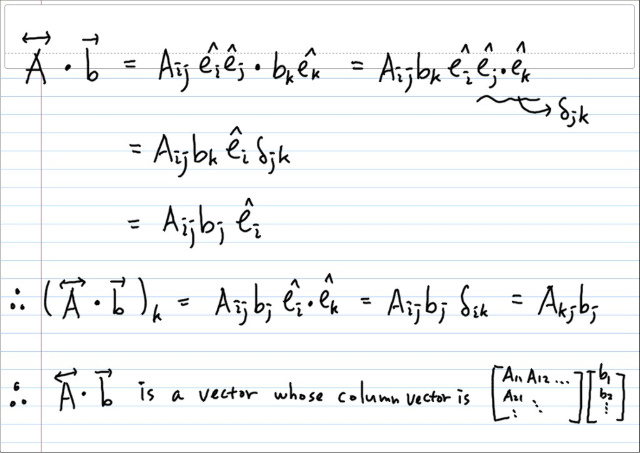
이경우에도 닷 프로덕트에 의해 랭크가 떨어지는 것을 확인 할 수 있다. 닷 프로덕트의 특징이다. 전체랭크합에 대해 두개씩 떨어뜨린다. 위의경우 A 가 2 , b 가 1 인데, 결과는 1 이다. 다이애드는 랭크를 올리고, 닷 프로덕트는 랭크를 떨어뜨린다.

텐서와의 닷 프로덕트를, 벡터의 성분들만 가지고 살펴보면, 곧바로 일차변환임을 알 수 있다. 결국 공간상에서 벡터의 방향까지 변하게 할 수 있다. 그냥 스칼라를 곱했다면, 크기( 음수=반대방향 포함 )만을 바꿀수 있을 것이다.
글이 상당히 길어졌는데, 마지막으로, 전자기학의 맥스웰 스트레스 텐서에 dyad 가 어떻게 등장하는지 살펴보면서 끝맺도록 하겠다.