직교좌표변환과 크로네커 델타

크로네커 델타의 정의는 다음과 같다.

즉, 같으면 1 , 다르면 0 인 기호다.


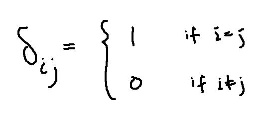
δ_ij 를 n x n 메이트릭스 δ의 i th row, j th column 의 성분으로 보면, δ 는 단위행렬이 된다.


또, 직교좌표변환에서, 오소노말 베이시스들의 내적과 관련해, 우리는 이미 다음과 같은 사실을 알고 있다.

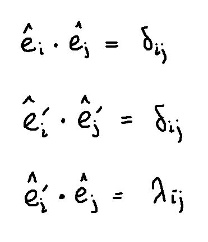
서메이션에서는 서메이션 안하는 첨자를 서메이션으로 포함시키는 트릭을 쓸때 매우 유용하다.

델타가 곱해져있으면 중복첨자를 나머지 다른 첨자하나로 바꾸고 델타 자신은 없어진다고 생각해도 좋다.



반대로 일부러 델타를 붙여서 수식을 조작하는 테크닉은 수식을 전개할때 자주 사용된다. 가령...

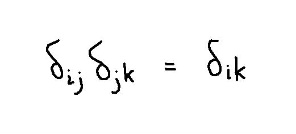
이제 직교좌표변환 행렬 λ 와 크로네커 δ 사이의 좀더 직접적인 관계식을 구해보자.

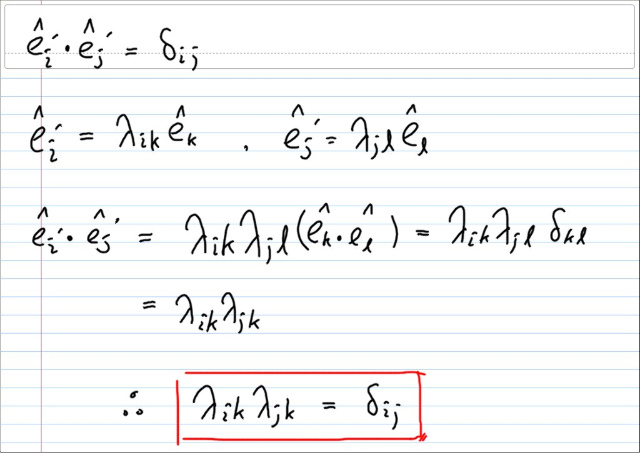
이 식에서도 마찬가지로, 중복인덱스는 캔슬링되고 중복되지 않는 인덱스만 살아남고있다.


이 수식을 보면, 좌표변환행렬의 같은행 같은열의 곱은 1 이고 행번호와 열번호가 다른경우는 곱하면 0 이 된다는 것을 알 수 있다.


참고로 e_i ' , e_j ' 내적으로 시작하지 않고, e_i , e_j 내적으로 시작하면 결론에서 람다의 중복인덱스가 앞쪽에 온다. 앞의것이 중복되든, 뒤의것이 중복되든, 크로네커 델타가 된다.