스케일러 (scalar) , 스칼라 - 좌표변환에 의한 정의

벡터의 좌표변환에 의한 정의와 마찬가지로, 스케일러도 좌표변환에 의해 정의할 수 있다.

스케일러는 그냥 어떠한 값이다. 따라서 그 값은 좌표변환에 무관하여야 한다.

그러므로, 좌표변환에 무관한 "값" 을 스케일러 라고 하겠다.  ( 방향은 없고, 값만 있다. )


혼동해서는 안되는 것이, 그 스케일러 값이 있는 좌표는 변해도 상관없다는 것인데, 가령, 위치벡터의 코오디네이트벡터를 좌표로 쓰는 경우, 좌표계를 회전시키면 좌표가 변한다. 그러나 그 지점에서 스케일러 값 자체는 변화가 없다.

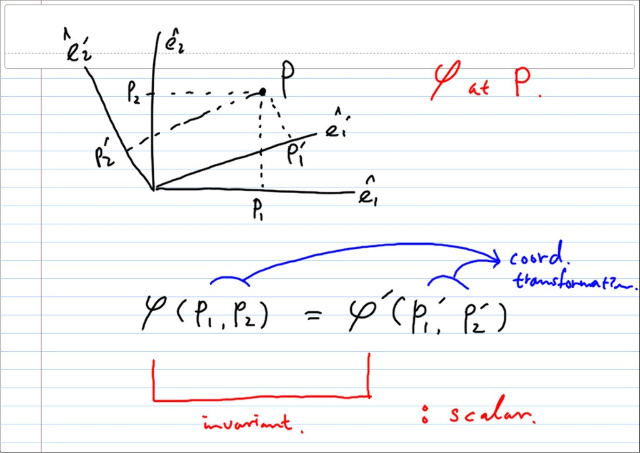
간단한 예로, 벡터의 크기가 스케일러임을 보이자.

벡터의 크기의 제곱은 벡터 대수적 표현으로 각 컴포넌트들의 제곱합이다. ( 단, 오소노말 베이시스 상에서...)


이제, 그것이 좌표변환에 대해 불변임을 보이면 된다.

제곱텀을, 제곱을 풀어서 같은것을 중복해서 곱한것으로 쓰겠다. 그러면, 자연스럽게 중복첨자가 되고, 따라서,서메이션 기호를 생략한다.

따라서, 벡터의 크기는 좌표변환에 대해 불변이고, 따라서, 정의에 의해, 스케일러이다.


똑같은 방식으로, 벡터의 내적은 스케일러 임을 보일 수 있다.