텐서(tensor) = 좌표변환 그리고 호모몰피즘(homomorphism)

텐서를 정의하는 많은 방법들이 있다. 그리고 그것들은 역시 각각의 케이스에 맞게 사용되어진다. 어떠한것을 정의로 사용하고 다른것들을 정리 등으로 사용하든지 그것들은 결국은 모두 동치가 될 것이다. ( ※ 주의.  꼭 그렇지만은 않다고 한다. 즉, 텐서의 경우에, 다르게 정의해서 다른 내용을 나타낼수도 있음.)


그중에 우리가 앞서 논의한 것과 같은 맥락으로 이야기를 하자면, 물리적 텐서란  좌표로부터 자유로운, 본질적인(essential) 물리량 이라고 할 수 있다.


정의를 제대로 하자면, 이것저것 덧붙여야 될 것들이 많은데, 벡터의 정의에서도 보았듯이, 현학적이게도, 수식이 등장하는 까닭에 그러한 것들은 논의상 생략하기로 하고, 필요할때마다 언급을 하기로 한다.


텐서가 좌표로부터 자유롭다는 것은 우리의 물리법칙이 텐서로 표현될 경우, 그 레프리젠테이션 역시도 좌표변환으로 부터 자유롭다는 것을 의미한다. 이는, 좌표변환에 아예 상관없다기 보다는 ( 물론 표현상 그렇게 말할수 있지만... ) 어떠한 좌표가 주어지던지 간에 동일한 form 으로 기술되며, 각각의 성분은 좌표에따라 deterministic 하게 결정됨을 의미한다.


가령, 베이시스가 β 인 좌표계에서 어떠한 물리법칙이 F = m a 로 기술되었다고 하자. 그런데, 이것을 임의의 다른 베이시스 β' 에서 기술한다면, F 는 F' 으로 코오디네이트가 바뀔것이고, 마찬가지로 m 은 m' 으로 (물론, m' = m 이어야 한다. ) , a는 a' 으로 바뀔것이다. 그리하여 우리는 β' 에서 F' = m' a' 이 되기를 기대한다.


그것이 본질적인 물리법칙이었다면 당연히 그렇게 되어야 할 것이다. 그렇지 않고, β' 에서는 F' = a' / m 이 된다면, 그것을 물리법칙이라고 할 수 있을까? ' 질량이 커지면 같은 가속도를 내는데 더 큰 힘이 필요해' , ' 그래? 고개를 조금 꺾으니, 질량이 커지면 같은 힘으로 더 큰 가속도를 낼수 있는걸로 보이는데? '  이렇듯, 단지우리가 좌표축을 어떻게 잡느냐에 따라 수백 수천개의 완전히 다른 statement 가 된다면, 우리는 그것을 물리법칙이라고 부를 수 없을 것이다.


이것은 마치, 같은 현상에 대해, 두가지 다른 언어로, 겉보기엔 다르게 표현하지만, "이상적인" 번역규칙이 있어, 그것들이 완벽하게  상호 번역되는 상황에 비유할 수 있다.


순간 Abstract Algebra 적인 향기가 느껴진다. 우리가 추상( <- 이 표현이 좀 그렇다. )대수학에서 얻은 핵심적 통찰중에, "같은 것은 같은 것이다" 라는 것이 있었다. 즉, 겉으로 보기에는 달라보여도, 그것들 사이에 isomorphism 이 있으면, 그것의 본질은 동일하다고 할 수 있는 것이다.


마찬가지로, 어떠한 물리법칙이 각 좌표에서 다르게 기술되더라도 그것의 본질은 같아야 한다는 점에서 좌표들 사이의 변환은 isomorphism 이어야 한다. isomorpishm 은 homomorphism + bijection 이므로, homomorphism 만 살펴보면 충분하다. 어차피 좌표변환은 bijection 이어야 하니까.


호모몰피즘이란 결국, map이 연산을 보존하는가에 대한 질문이다.

즉, 연산을 하고 맵을 하는것과, 맵을하고 연산을 하는 것이 같아야 한다는 것이다.


좌표변환 λ가 homomorphic map 이면,  β 에서  α = * ( α1 , α2 , ... )  로 기술된 어떠한 물리법칙이 β ' 에서 어떻게 기술되는지 살펴보자.

즉, β' 에서도 같은 형태로 기술됨을 볼 수 있다. 어떤의미로, 변환의 호모몰피즘은 텐서의 본질중에 하나이기도 하다.



이미, 우리는 벡터가 좌표로 부터 자유로운 양임을 확인했고, 스케일러역시 좌표변환에 무관한 "값"으로 재정의했으므로, 좌표로 부터 자유롭다. 결론적으로, 벡터와 스케일러 역시 모두 텐서의 범주에 포함된다. 대수적으로는 스케일러를 레프리젠트 하기위해서 우리는 하나의 문자가 필요했고, 벡터를 레프리젠트 하기 위해서는 n-tuple 이 필요했다. 마찬가지로 한차원 하이어 오더에 대해, 텐서를 레프리젠트 하기 위해서는 메이트릭스가 필요하다. 어떠한 레프리젠테이션을 갖던지, 중요한것은 좌표변환에 대해 같은 일관된 폼을 유지하는 것이다.



벡터가 n-tuple 레프리젠테이션을 갖었을때, 우리는 그것이 베이시스와 결합해서 하나의 완결된 정보라는 것을 확인했다. 마찬가지로, 메이트릭스로 표현된 텐서도 베이시스와 결합해서 하나의 완결된 정보가 된다. 그래서, 어떤 베이시스에 대응하는 메이트릭스 레프리젠테이션을 알고 있으면, 그걸로 완결하며, 임의의 어떠한 베이시스가 주어져도 그에 대응하는 메이트릭스는 자동으로 결정된다. 즉, 공식을 통해 성분변환을 할 수 있다.



이제, 텐서의 메이트릭스 레프리젠테이션을 살펴보고, 임의의 좌표에대해 어떻게 변환하는지 살펴보자.


어떠한 물리법칙, 가령 ->F = m  a->  를 생각해보자. F 는 힘의 벡터이고, a는 가속도의 벡터이다. 이것은 F 라는 인풋에 대해 a 라는 아웃풋이 나오고 질량은 비례상수라고 볼 수 있다. 즉 F 에서 a 로의 변환으로 볼 수 있다. 특히, m 이 스케일러이므로 a는 F와 평행하다.


그런데, 모든 물리법칙이 꼭 그래야 할 필요는 없다. 평행하지 않은 경우도 포함할 수 있다면 그것이 더 일반성을 갖을 것이다.


아웃풋벡터와 인풋벡터가 평행하지 않은 예를 살펴보자.


CO2 분자에 전기장을 걸면, 그로부터 유도되는 폴러라이제이션은 CO2 의 모양으로 인해, 축방향과 그렇지 않은 방향이 다를수 밖에 없다. 러프하게, 축방향에 수평한 전기장에 의해 수평성분의 폴러라이제이션이 생긴다고 가정하고, 수직방향의 전기장에 의해 수직방향의 폴러라이제이션이 생긴다고 가정하자.

수직성분에 대한 팩터와 수평성분에 대한 팩터가 다르므로, 결과적으로 인풋과 평행하지 않은 아웃풋 벡터가 나온다.

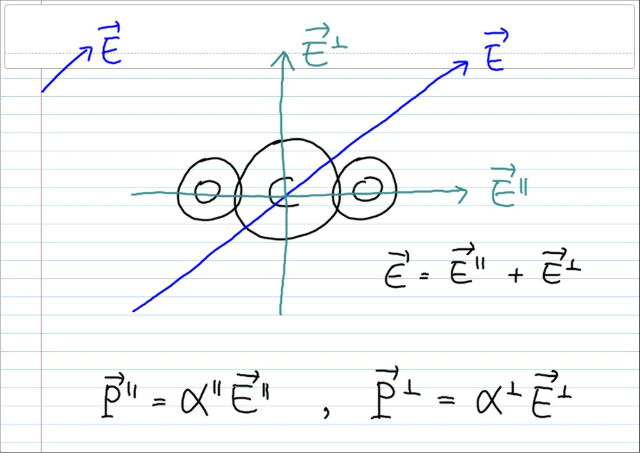
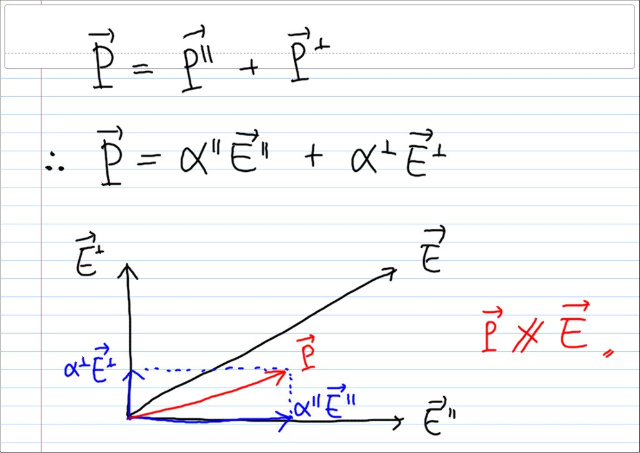
해당 축방향의 전기장만이 해당 축방향의 폴러라이제이션에만 영향을 미친다고 했음에도 불구하고, 인풋벡터와 아웃풋벡터가 평행하지 않다. 따라서, 우리는 이것을 일반적인 것으로 받아들인다.


일반적으로, 인풋과 평행하지 않은 아웃풋이 생성된다는 것은, 아웃풋 입장에서 보면, 아웃풋과 평행하지 않은 벡터의 영향을 받는다는 뜻이다. 수직한 벡터에 의해서도 영향을 받는다.


이제, 인풋과 아웃풋 모두, 베이시스에 대해 직교분해를 하자. 그러면, 각 아웃풋은 각 인풋에 의해 모두 영향을 받을 수 있으므로, 그것을 모두 고려하면 총 9개의 팩터가 필요하다.

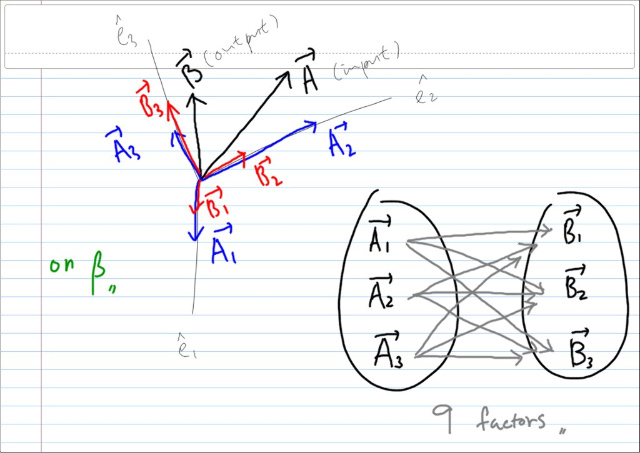
각각 아웃풋은 모든 인풋에 의한 영향을 모두 더해줘야 한다.

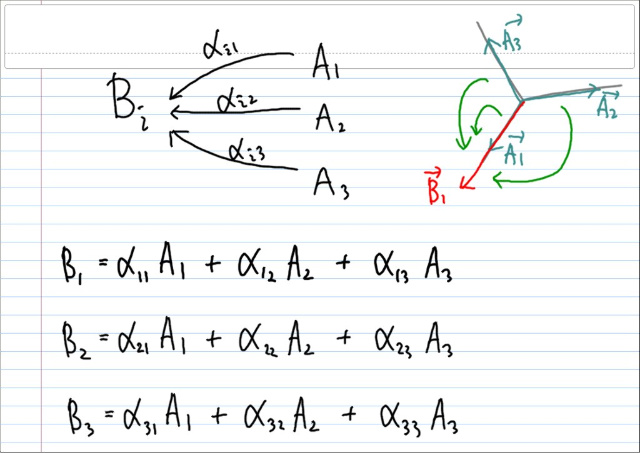
따라서, 행렬형태로 쓰면...

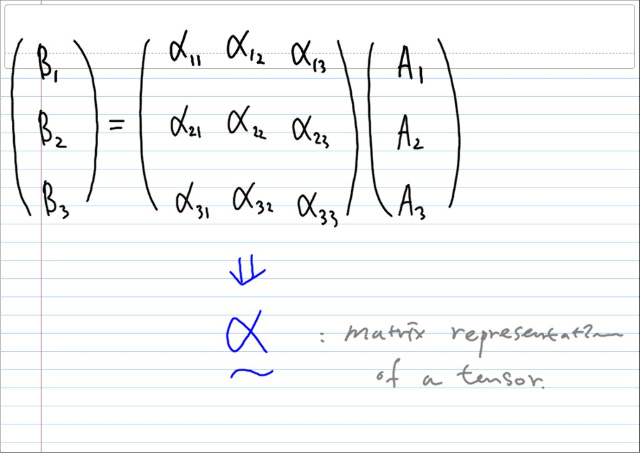
텐서임을 표시하기 위해, 밑에 물결을 했지만, 표준 노테이션도 없을뿐더러 매우 귀찮기 때문에 오해의 소지가 없는한 그냥 문자하나로 표시하도록 하겠다.


어떠한 베이시스 β 상에서, 어떠한 물리법칙이 B=αA 으로 표현되었다고 하자. A 와 B는 벡터를 레프리젠트 하는 n-tuple 이고, α 는 텐서를 나타내는 행렬이라고 하자.

A를 일종의 input , B 를 일종의 output 으로 보고, 그것을 어떠한 물리법칙을 나타낸다고 보아도 좋다.

베이시스 β' 으로의 직교좌표변환을 λ 라고 놓고, 변환에 따른 α 의 성분변화를 고려해보자.

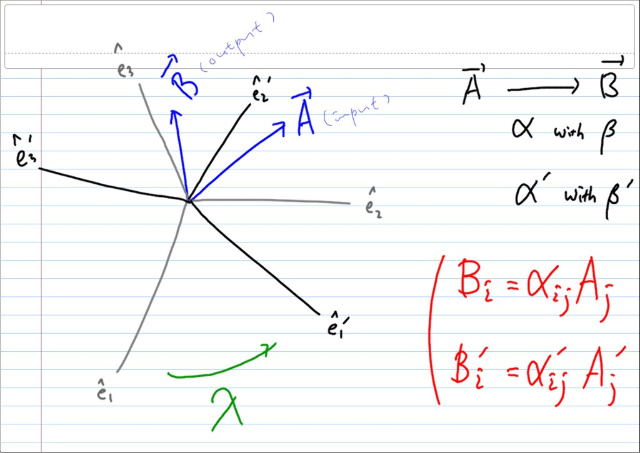
좌표축을 β' 로 잡은 사람에게도 해당 물리법칙은 동일한 형태로 기술되어야 한다. 단지, β' 로 잡은 사람에게는 A가 A' 으로 표현될 뿐이고(물론 물리적으론 동일한 벡터이다, 단지 코오디네이트만 다르게 표현된다.) B 가 B' 으로 표현될 뿐이고, α가 α' 으로 표현될 뿐이다. 결과적으로, 각각의 성분만 변할뿐, 물리법칙에 대한 레프리젠테이션은 동일한 폼을 유지해야 된다.


α' 의 각 엔트리들이 어떻게 디터미니스틱하게 결정되는지 살펴보자.

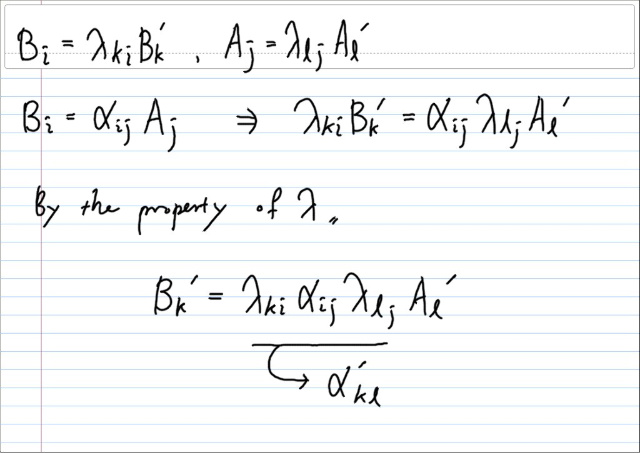
위에서, 람다가 서메이션으로 곱해져있을때, 마치 아무런 제약없이 이항하는것처럼 보이는 성질을 이용했다. (참고 : 좌표변환행렬의 캔슬레이션 law ) 또한, 서메이션내에서 각각의 성분은 스케일러고 교환법칙이 성립하므로, 순서를 바꿀수 있다.

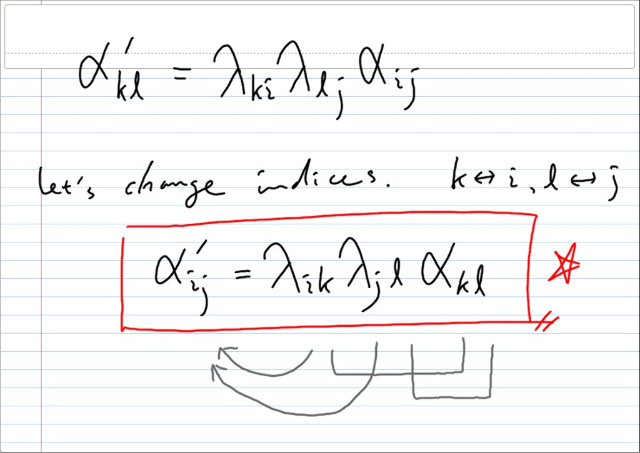
마지막엔 그냥, 구하고자하는 텐서의 첨자를 i,j 로 놓기위해, 첨자를 바꿨다. 아무튼, 여기서도 중복첨자는 죽고, 중복되지 않은 것만 살아남은것을 확인할 수 있다.


요컨대... 우리가 텐서 메이트릭스 레프리젠테이션 α 와 베이시스 β 의 짝만 가지고 있다면, 이는 좌표로 부터 자유로운 완결한 정보인것이며, 임의의 어떠한 베이시스 β' 에 대해서도 위의 변환식에 따라, α' 을 항상 구할 수 있고, 그에의해 어떠한 물리법칙을 좌표로 부터 자유롭게, 동일한 폼으로 기술할 수 있게된다.