수학과 물리학 그리고 벡터의 정의 (2편) - 직교 좌표회전행렬 ( 성분변환행렬 )
Physics/Math./Mech./Gen. Relativity2008. 12. 21. 00:10 |벡터스페이스에 대해 약간의 불만을 품고 논의를 시작했지만, 그렇다고 해서 벡터스페이스 자체를 부정하는 것은 아니다. 벡터스페이스는 더 넓은 개념이고, 우리는 추가적인 조건을 덧붙이므로써 물리적벡터로 제한하려 한다. 따라서, 벡터스페이스의 개념들을 그대로 가져다 쓸 수 있다. (물리적벡터라는 어색한 말을 굳이 쓰고 있는 이유는 벡터스페이스의 일반화된 벡터개념때문이다. 앞으로 혼용해서 두서없이 쓰더라도 이해를 바란다.)
어떠한 n-tuple이 물리적벡터를 레프리젠트 하기 위해서는, 베이시스 (어떤 odered set) 역시도 물리적벡터들로 구성되어야 할 것이 요구된다. 가령, 베이시스가 { 감귤, 사과, 복숭아 } 인 경우 어떠한 triple 도 물리적벡터를 표현할 수가 없다.
- 이 설명에 대해서는 논란의 여지가 있음을 밝혀둔다. 순환논리에 빠졌기 때문이다. 그러나 너무 걱정할 필요는 없다. 우리는 감각적으로 벡터라는 것을 느낄수 있다고 치고, 그러한 상황에서, 어떠한 n-tuple 이 물리적 벡터를 레프리젠트 하기 위한 조건을 찾고 있는 과정일 뿐이다. 지금 단계에서 이러한 모호성은 어쩔 수가 없다. 종국에 이르러 이러한 문제는 해결된다.
물리적벡터가 방향을 갖는 고유한 물리량이라고 했으므로, 그 자체는 좌표계에 무관해야 한다. 우리가 임의로 어떤 좌표축을 잡던지 벡터입장에서 알게 뭔가 ?
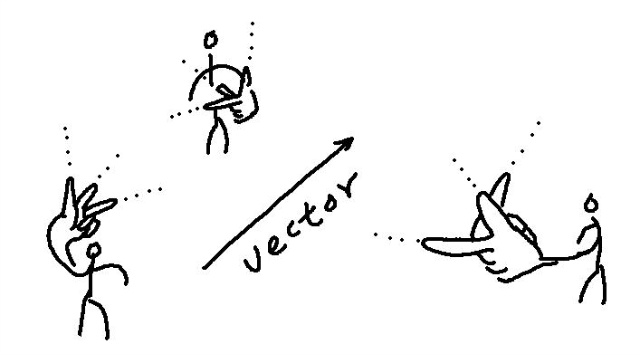
위 세사람은 각기 다른 좌표축을 잡았기 때문에 각기 다른 triple 로 같은 벡터를 나타내게 될 것이다. 같은 벡터에 대해 어떤이는 (1,3,4) 라고 말할 것이고, 어떤이는 (-3,4,9) 이라고 말할 것이고, 또 어떤이는 (4,5,7) 이라고 말할 것이다. ( 유닛 베이시스가 아니므로 제곱합들이 같을 필요는 없다. )
이것은 무엇을 말해주는가. 이는 n-tuple 이 오직 베이시스와 짝을 이룰때에만 비로소 벡터를 완전하게 나타낼수 있음을 보여준다. 위의 세사람이 비록 서로 다른 ordered triple 들을 가지고 말할지라도, 각자 그때의 베이시스와 결합시키면 모두 동일한 벡터를 나타내게 될 것이다.
어떤 물리적벡터 ->a 를 고려하자. 베이시스 β = { ->e_1 , ->e_2 , ... } 에 대해 ordered n-tuple ( a_1 , a_2 , ... ) 가 ->a 를 레프리젠트한다고 하자. 이 n-turple 을 β 에 대응되는 ->a의 coordinate vector 라고 부르자. 당연히, 코오디네이트 벡터는 물리적벡터가 아니다. 코오디네이트벡터와 베이시스는 다음과 같이 결합하여 물리적 벡터 ->a 가 된다.
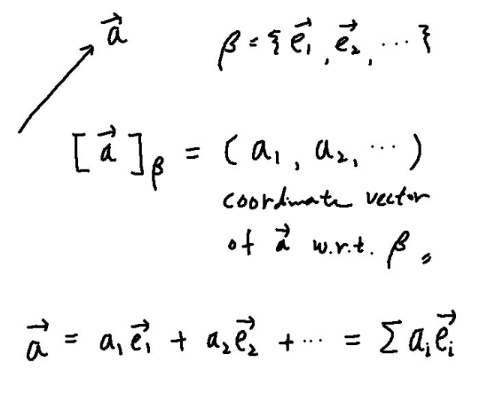
베이시스를 구성하는 벡터각각을 기저벡터(베이시스 벡터) 라고 하면, 코오디네이트 벡터는 베이시스벡터들의 선형조합에 대한 정보(즉, 계수들) 이다. 베이시스벡터들을 어떻게 잘 섞어서 해당벡터를 만들어 낼 것인가에 대한 레서피인것이다. 아마도 당신은 여기서 푸리에 계수를 떠올릴수도 있다.
코오디네이트벡터와 베이시스의 결합은 벡터 그 자체이므로, "코오디네이트벡터와 베이시스의 짝"은 벡터를 완전하게 표현하며, 따라서 그 짝은 임의의 좌표축에 무관한 본질적 정보이다. 어떠한 임의의 베이시스에 대해서도 그에 대응되는 코오디네이트벡터는 decisively 결정된다는 말이다.
다소 현학적으로 보이겠지만, 결과적으로 이 변환공식이 물리적벡터의 대수적 정의의 핵심이 된다.
이제 변환공식을 구해보자.
단, 우리가 다룰 변환은 원점이 고정된 오소노말 베이시스의 회전이다. 트랜슬레이셔널 변환의 경우, 베이시스에 변화가 없으므로 어차피 무의미하다. 위치벡터나 기준틀의 운동문제를 좌표계와 묶기 전까지는 논외로 한다.
어떠한 벡터 A에 대해 코오디네이트벡터와 베이시스 β 를 알고 있는 상태에서, 어떤 임의의 베이시스 β' 에 대한 코오디네이트 벡터를 구해보자. 단 위에서도 말했듯이, β 와 β' 모두 오소노말 베이시스로 한다.
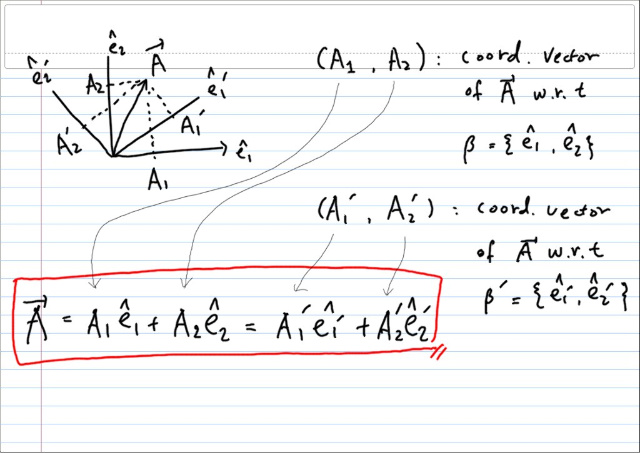
즉, 벡터자체는 그대로인데, 좌표축을 어떻게 잡아주느냐에 따라, coordinate vector 가 달라진다. 이제, (A1,A2) 와 (A1' , A2 ' ) 사이의 변환관계만 유도하면 된다. 차원을 높여서 일반화 시키는 것도 간단하다.
다음과 같은 관계를 알 수 있다.
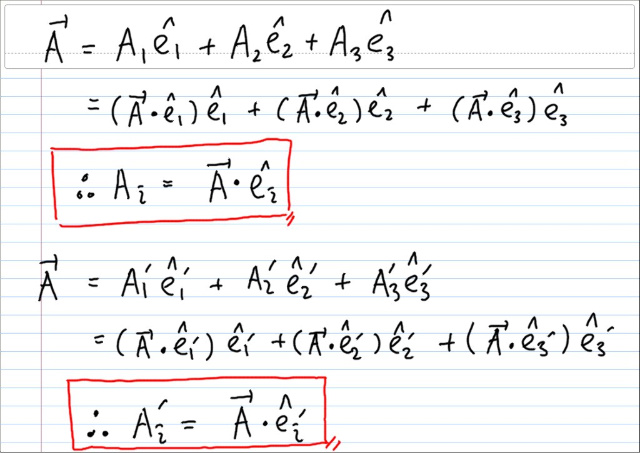
각 축에 대한 컴포넌트를 내적만으로 바로 구할수 있는것은 베이시스가 오소노말이기 때문이다.
이제 Ai' 을 Ai 로 부터 구해보자.
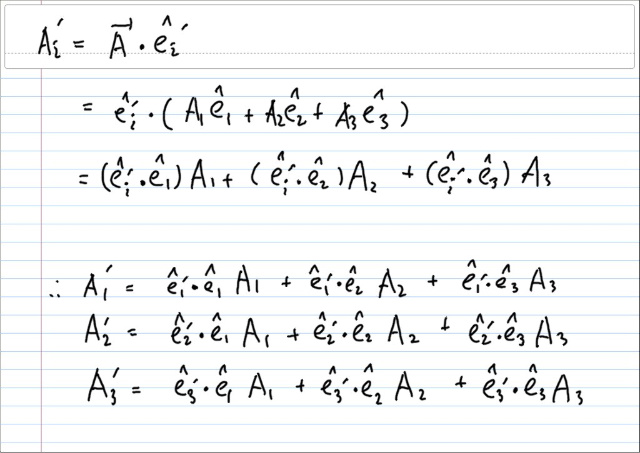
코오디네이트 벡터를 컬럼벡터로 써도 좋고 로우벡터로 써도 좋다. 어차피 물리적벡터가 되려면 베이시스와 결합을 해야 한다. 위의 형태에서 그대로 쓰기엔 컬럼벡터가 편해보이니 대개의 경우처럼 컬럼벡터로 쓰자.
그러면 직교 좌표회전행렬은 다음과 같이 구해진다.

람다는 디렉션코사인으로 두 벡터의 내적을 두 벡터의 놈으로 나눈거다. 직교 좌표회전행렬의 ij 성분이 디렉션코사인 람다ij 이므로 직교 좌표회전행렬 간단히 λ 라고 둘 수 있다. 나중에 보이겠지만, 두개의 베이시스 β , β' 가 오소노말이면 위와 같은 행렬 λ 는 다음을 만족한다. transpose( λ ) λ = I . 따라서, |λ| = ± 1 이 된다. + 1 인경우를 proper rotation 이라고 하고, -1 인경우 inversion 이 포함된 회전으로 improper rotation 이라고 한다.
이제 어떠한 벡터스페이스의 요건을 충족시키는 n-tuple = ( A1, A2, ... ) 에 대하여, 이것이 물리적벡터를 레프리젠트 한다면, 직교 회전변환에 대해 n-tuple 의 성분은 위에서 컨스트럭션 한 λ 에 의해 다음과 같이 변환 되어야 할 것이다.

이제 우리는 물리적의미를 갖는 벡터를 다음과 같이 정의할 수 있다.
어떠한 벡터스페이스의 엘레멘트에 대해, orthonormal rotation 에 대한 코오디네이트 변화가 위와 같이 변할때, 그것을 Rank 1 텐서로서의 벡터라고 한다.
( 참고로, 위에서 직교 베이시스들의 회전에 대응하여 구한 회전행렬이 직교행렬임을 다음과 같이 쉽게 보일수 있다. )

( 한번더 참고로, 이 직교 조건은 유니타리의 특수한 경우로 생각할 수 도 있다. )
어떠한 n-tuple이 물리적벡터를 레프리젠트 하기 위해서는, 베이시스 (어떤 odered set) 역시도 물리적벡터들로 구성되어야 할 것이 요구된다. 가령, 베이시스가 { 감귤, 사과, 복숭아 } 인 경우 어떠한 triple 도 물리적벡터를 표현할 수가 없다.
- 이 설명에 대해서는 논란의 여지가 있음을 밝혀둔다. 순환논리에 빠졌기 때문이다. 그러나 너무 걱정할 필요는 없다. 우리는 감각적으로 벡터라는 것을 느낄수 있다고 치고, 그러한 상황에서, 어떠한 n-tuple 이 물리적 벡터를 레프리젠트 하기 위한 조건을 찾고 있는 과정일 뿐이다. 지금 단계에서 이러한 모호성은 어쩔 수가 없다. 종국에 이르러 이러한 문제는 해결된다.
물리적벡터가 방향을 갖는 고유한 물리량이라고 했으므로, 그 자체는 좌표계에 무관해야 한다. 우리가 임의로 어떤 좌표축을 잡던지 벡터입장에서 알게 뭔가 ?

위 세사람은 각기 다른 좌표축을 잡았기 때문에 각기 다른 triple 로 같은 벡터를 나타내게 될 것이다. 같은 벡터에 대해 어떤이는 (1,3,4) 라고 말할 것이고, 어떤이는 (-3,4,9) 이라고 말할 것이고, 또 어떤이는 (4,5,7) 이라고 말할 것이다. ( 유닛 베이시스가 아니므로 제곱합들이 같을 필요는 없다. )
이것은 무엇을 말해주는가. 이는 n-tuple 이 오직 베이시스와 짝을 이룰때에만 비로소 벡터를 완전하게 나타낼수 있음을 보여준다. 위의 세사람이 비록 서로 다른 ordered triple 들을 가지고 말할지라도, 각자 그때의 베이시스와 결합시키면 모두 동일한 벡터를 나타내게 될 것이다.
어떤 물리적벡터 ->a 를 고려하자. 베이시스 β = { ->e_1 , ->e_2 , ... } 에 대해 ordered n-tuple ( a_1 , a_2 , ... ) 가 ->a 를 레프리젠트한다고 하자. 이 n-turple 을 β 에 대응되는 ->a의 coordinate vector 라고 부르자. 당연히, 코오디네이트 벡터는 물리적벡터가 아니다. 코오디네이트벡터와 베이시스는 다음과 같이 결합하여 물리적 벡터 ->a 가 된다.
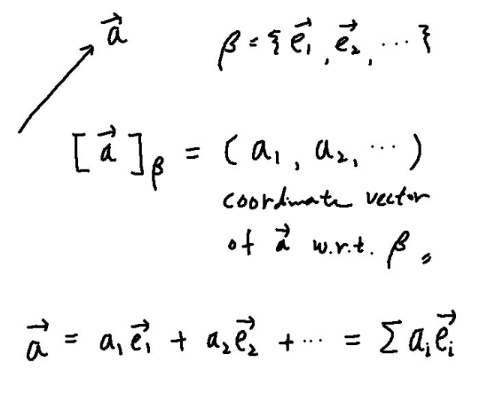
베이시스를 구성하는 벡터각각을 기저벡터(베이시스 벡터) 라고 하면, 코오디네이트 벡터는 베이시스벡터들의 선형조합에 대한 정보(즉, 계수들) 이다. 베이시스벡터들을 어떻게 잘 섞어서 해당벡터를 만들어 낼 것인가에 대한 레서피인것이다. 아마도 당신은 여기서 푸리에 계수를 떠올릴수도 있다.
코오디네이트벡터와 베이시스의 결합은 벡터 그 자체이므로, "코오디네이트벡터와 베이시스의 짝"은 벡터를 완전하게 표현하며, 따라서 그 짝은 임의의 좌표축에 무관한 본질적 정보이다. 어떠한 임의의 베이시스에 대해서도 그에 대응되는 코오디네이트벡터는 decisively 결정된다는 말이다.
다소 현학적으로 보이겠지만, 결과적으로 이 변환공식이 물리적벡터의 대수적 정의의 핵심이 된다.
이제 변환공식을 구해보자.
단, 우리가 다룰 변환은 원점이 고정된 오소노말 베이시스의 회전이다. 트랜슬레이셔널 변환의 경우, 베이시스에 변화가 없으므로 어차피 무의미하다. 위치벡터나 기준틀의 운동문제를 좌표계와 묶기 전까지는 논외로 한다.
어떠한 벡터 A에 대해 코오디네이트벡터와 베이시스 β 를 알고 있는 상태에서, 어떤 임의의 베이시스 β' 에 대한 코오디네이트 벡터를 구해보자. 단 위에서도 말했듯이, β 와 β' 모두 오소노말 베이시스로 한다.

즉, 벡터자체는 그대로인데, 좌표축을 어떻게 잡아주느냐에 따라, coordinate vector 가 달라진다. 이제, (A1,A2) 와 (A1' , A2 ' ) 사이의 변환관계만 유도하면 된다. 차원을 높여서 일반화 시키는 것도 간단하다.
다음과 같은 관계를 알 수 있다.
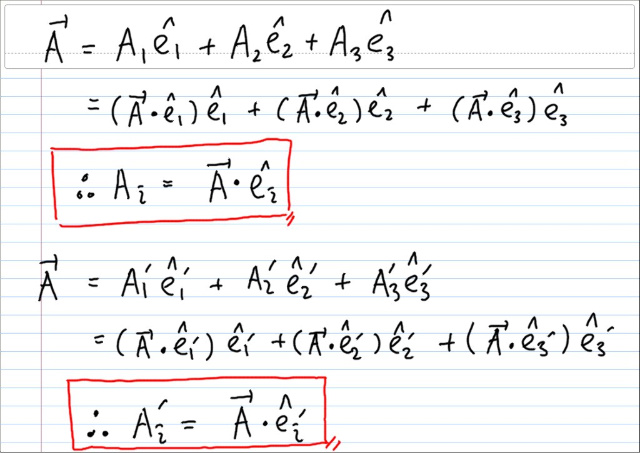
각 축에 대한 컴포넌트를 내적만으로 바로 구할수 있는것은 베이시스가 오소노말이기 때문이다.
이제 Ai' 을 Ai 로 부터 구해보자.
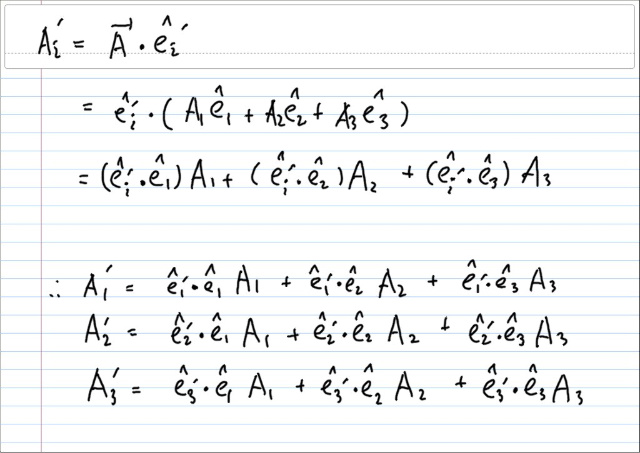
코오디네이트 벡터를 컬럼벡터로 써도 좋고 로우벡터로 써도 좋다. 어차피 물리적벡터가 되려면 베이시스와 결합을 해야 한다. 위의 형태에서 그대로 쓰기엔 컬럼벡터가 편해보이니 대개의 경우처럼 컬럼벡터로 쓰자.
그러면 직교 좌표회전행렬은 다음과 같이 구해진다.

람다는 디렉션코사인으로 두 벡터의 내적을 두 벡터의 놈으로 나눈거다. 직교 좌표회전행렬의 ij 성분이 디렉션코사인 람다ij 이므로 직교 좌표회전행렬 간단히 λ 라고 둘 수 있다. 나중에 보이겠지만, 두개의 베이시스 β , β' 가 오소노말이면 위와 같은 행렬 λ 는 다음을 만족한다. transpose( λ ) λ = I . 따라서, |λ| = ± 1 이 된다. + 1 인경우를 proper rotation 이라고 하고, -1 인경우 inversion 이 포함된 회전으로 improper rotation 이라고 한다.
이제 어떠한 벡터스페이스의 요건을 충족시키는 n-tuple = ( A1, A2, ... ) 에 대하여, 이것이 물리적벡터를 레프리젠트 한다면, 직교 회전변환에 대해 n-tuple 의 성분은 위에서 컨스트럭션 한 λ 에 의해 다음과 같이 변환 되어야 할 것이다.

이제 우리는 물리적의미를 갖는 벡터를 다음과 같이 정의할 수 있다.
어떠한 벡터스페이스의 엘레멘트에 대해, orthonormal rotation 에 대한 코오디네이트 변화가 위와 같이 변할때, 그것을 Rank 1 텐서로서의 벡터라고 한다.
( 참고로, 위에서 직교 베이시스들의 회전에 대응하여 구한 회전행렬이 직교행렬임을 다음과 같이 쉽게 보일수 있다. )

( 한번더 참고로, 이 직교 조건은 유니타리의 특수한 경우로 생각할 수 도 있다. )
