수학과 물리학 그리고 벡터의 정의 (1편)

물리학자가 어떤 아이디어를 내면, 많은 경우 수학자들에 의해 정교하게 다듬어진다. 때때로 그것은 수학의 새로운 분야를 창조하기도 한다. 근데 어쩔땐 다듬어 지는 과정에서, 물리학자들이 썩 반기지 않는 방식으로 다듬어 지는 경우가 있다. ( 여기서 물리학자랑 수학자를 나누는 것 자체가 애매하고 무의미하기도 한데, 그냥 말이 그렇다는 거다. )
 


벡터 이야기를 해보자. 벡터는 종종 수학과 물리학에서 그 정의를 달리하는데, 뭐 항상 그런건 아니고, 정의를 다르게 할때가 있다. 왜 그런 차이가 생기는 지에 대해서 살펴보자.



물리학은 아마도  벡터가 역학적인 컨셉을 내포하길 바랄 것이다. 크기와 방향이라는...



그런 의미에서 우리가 일반물리에서 배운 벡터의 개념은 바라던 바를 상당히 잘 표현하는 개념이라고 하겠다. 우리는 언제든지 공간상에 짝대기 하나긋고 화살표 찍찍 그으면 원하는 바를 표현할 수가 있다. 그리고 그것은 하나의 고유한 물리량이다 !!



그런데, 이른바 "벡터 알지브라" 라는 녀석으로 인해, 벡터는 "자유로움으로부터 까칠함으로" 마음을 고쳐먹는다. 가령, 내적의 경우, 우리는 그것을 초등 기하만으로 자연스럽게 받아들일 수 있지만, 벡터 알지브라를 만나면서 졸지에 AxBx + AyBy + AzBz 와 같은 수식으로 변해버리고, 밑장빼기 하다가 걸리지만 않으면 초딩도 쓴다는 외적도 벡터 알지브라를 만나면서 심오한척 분위기를 잡는다. 뭐 그래도 좋다. 아직 그것이 방향을 잃은 것은 아니니까. 당신의 풀이에 그 어떠한 그림도 없음을 자랑스러이 여겨도 좋다.



그러나, 벡터스페이스에 이르러서는, 덧셈을 동반한 몇개의 규칙과 더불어 벡터는 단지 n-tuple 로 전락(?)하게 된다. 벡터 어디션 , 스케일러 멀티플리케이션 에 관한 몇가지 약속만 만족시켜주면 n-tuple 은 n차원 벡터라는 명칭을 부여받게된다. ( 목적에 따라서는 n차원으로 확장된 이 벡터 개념은 여전히 획기적이고 유용한 개념임에는 틀림없다. )



그러나, 단지 n개의 숫자열이 벡터라는것을 못마땅하게 여기는 사람들도 있다. 그리피스의 표현에 따르면 (정확하게는 기억이 안나지만) , "사과 6개, 감귤 4개, 복숭아 7개"  저기...이것도 벡터라고 불러야 되나요? 라고 묻고 싶은거다.  벡터스페이스의 조건을 만족시키는게 겉으로 보이는 개수(11개였나?) 와는 달리 의외로 쉽다.


( 6 , 4, 7 )   : 사과 6개, 감귤 4개, 복숭아 7개.        ( 2 , 1, 2 )   : 사과 2개, 감귤 1개, 복숭아 2개.
( 6 , 4, 7 )  + ( 2 , 1, 2 )  =  ( 8 , 5, 9 )   :    사과 6개, 감귤 4개, 복숭아 7개와 사과 2개, 감귤 1개, 복숭아 2개 를 더하면 사과 8개, 감귤 5개, 복숭아 9개.   벡터 어디션(?) 완료.


2 ( 6 , 4, 7 ) =  ( 12 , 8, 14 )  : 사과 6개, 감귤 4개, 복숭아 7개. 를 두배하면 사과 12개, 감귤 8개, 복숭아 14개.
스케일러 멀티플리케이션 완료.  등등....


뭐, 좀 우스갯 소리 같지만, 실제로 이러한 벡터의 개념은 선형대수에서 아주 적절하게 쓰이고 있다 !
여기서 물리학이 좀 빈정이 상한거다. 사과, 감귤, 복숭아한테 방향이라니... 이건 좀 너무 물리와 동떨어진 것 아닌가 !

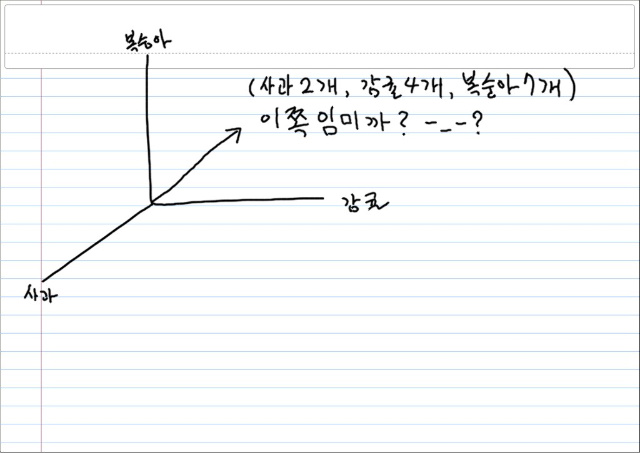
위 그림에서 보는것과 같이, 사과2개, 감귤4개, 복숭아 7개에 의해 부여해준 벡터 ( 2, 4, 7 ) 이 진짜로 "저~쪽" 을 가리켜야 할 이유는 없다. 즉, 저 벡터는 "물리적인 방향"을 가리키는 것이 아니다. 순수하게 도구적으로 사용되고 있달까?



우리의 물리학은 벡터를 고유한 "일종의" 물리량으로 간직하고 싶은거다. 저쪽 방향이 진짜 "저쪽"이길 바라는 마음?



우주 공간상에 떠있는 하나의 화살표를 상상해보자. 그리고 방향을 느껴보자. 그리고 그것이 복숭아나 사과의 개수와는 다름을 느껴보자.


이렇게 해서 나온것이 벡터의 텐서적 정의가 되겠다.  그리하여 벡터는 랭크 1인 텐서로 거듭나게 되는것이다. 길어진 관계로 여기서부턴...

다음편에 계속...