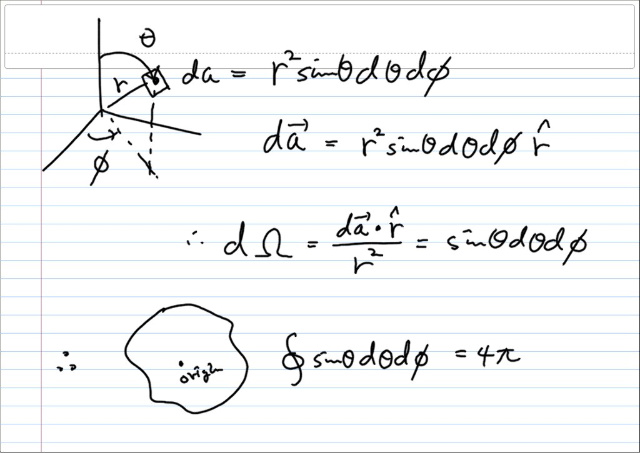[입체기하] 솔리드 앵글 ( solid angle , 입체각 )
Math/Geometry2008. 11. 29. 17:32 |물리 관련 포스팅을 좀 많이 하고싶은데, 어떤 말을 하고 싶어도 한번에 그걸 다 말하려면 포스팅이 너무 길어진다는 문제가 있다. 한번은 "좌표변환, 벡터 그리고 텐서" 라는 제목으로 글을 시작한적이 있느데, 글이 너무 심하게 길어져서 도저히 못쓰겠더라.
그래서, 얘기를 할때 편하도록 미리 언급해 두고 싶은 몇몇 단편적인 것들이 있다. 내용의 핵심이거나 뭔가 깊은 통찰을 주는것은 아니지만, 나중에 본론을 이야기할때 곁가지에 대한 부담을 덜어주고 글이 컴팩트해지도록 도움을 주기 때문이다. 하이퍼링크만 걸어주면 된다.
이미 감마펑션은 간단히 언급을 해놨고, 더블팩토리얼도 언급을 해놨으니, 바이노미얼 코이피션트만 언급을 하면 르장드르 폴리노미얼이나 베셀펑션을 언급할때 한결 간결해질것임은 분명하다. 그러한 단편들이 몇개 더 있는데, 가령, 디랙 델타펑션과 다이버젼스의 관계 라던가, 솔리드앵글 같은 것들이다.
여기선, 솔리드 앵글에 대해서 간단하게 미리 언급을 해두고 싶다.
레이디언( radian , 라디안)을 먼저 생각해보자. 어차피 각도라고 하는건 얼만큼 벌어져 있는가를 나타내는 지표일 뿐이다. 한바퀴를 360도로 보는것도 편리한 면이 많지만, 라디안은 그 이름에서 보듯이 radi - an , 반지름을 세는 단위로 쓴다.
어떠한 반지름을 잡고 빙둘러서 원을 그리면, 그 둘레에 지름이 몇개 들어가는가 (원주율) 에 대한 연구는 매우 오래된 것으로, 대략 3개가 들어가고 좀 남는다고 한다. 즉 반지름의 단위로 세면 6개들어가고 좀 남는것이다. 따라서 한바퀴라는 것은 360도라고 불러도 되지만, "6점몇 반지름" 이라고 불러도 똑같은 것이다. 여기서 저 "반지름" 이라고 부르는 것이 바로 라디안의 본질이다.
( 여기서 잠시 딴소리를 하자면, 중1때 열심히 외웠던 "원의 둘레 = 2 π r " 이라는 공식은 단지 원주율의 정의에 불과할뿐, 그 이상도 그 이하도 아니다. 차라리, 어깨너머로 줏어들은 파이는 무리수라 카더라는 것과 조합해서, "원의 둘레가 유리수라면 반지름은 무리수여야 겠군요" 같은게 더 유익하다고 하겠다. )
아무튼, 라디안은 둘레길이를 반지름으로 나눈것과 같으므로, 무차원이지만 내막은 길이/길이 가 되겠다. 또한 반지름으로 나누니까 반지름 1 인 원으로 축소시키면 호의 길이가 곧바로 각도가 될 것이다. ( 단, 무차원이다 )
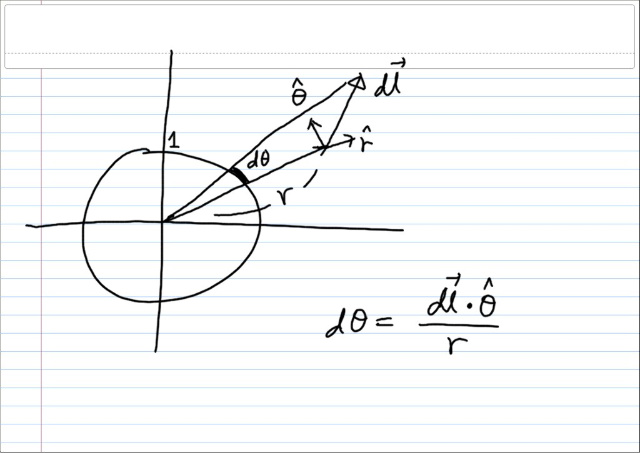
그림으로 보면, 다음과 같이 나타낼 수 있다.
미소각도를 살펴보자.
즉, 어떤 미소길이를 반지름에 수직하게 사영으로 돌려서 다시 반지름으로 나눠 반지름1인 원으로 스케일링 시키면 미소각도가 된다. 차원을 잠시 보자면, 단위벡터는 무차원이므로, 분모분자 모두 길이차원이고 따라서 dθ 도 무차원, 잘 맞는다.
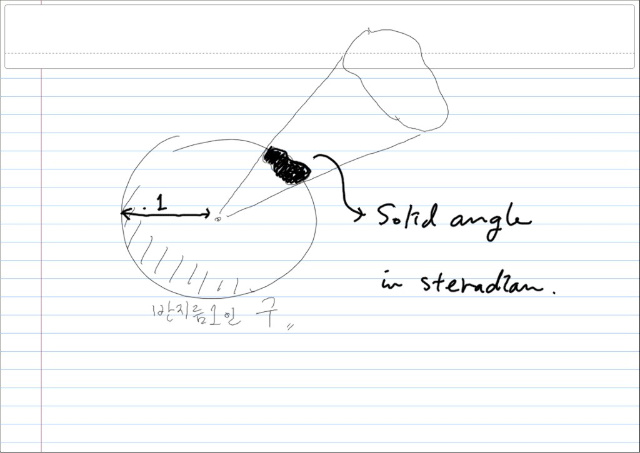
이제, 이러한 개념을 확장해서 솔리드앵글, 즉 입체각을 정의하자. 다음의 그림을 보자.
플레인 앵글은 한바퀴는 반지름 1인 원 둘레이므로 2π 인반면, 솔리드 앵글은 반지름 1인 구면이므로 전체각도가 4π 가 된다. 단위는 steradian 을 쓰고, 반지름 1인 구면상에서 면적 1인 입체각도가 1 steradian 이 된다. 입체각 역시 무차원이고, 그 내막은 면적/면적이다.
이번에도 미소입체각을 살펴보자.
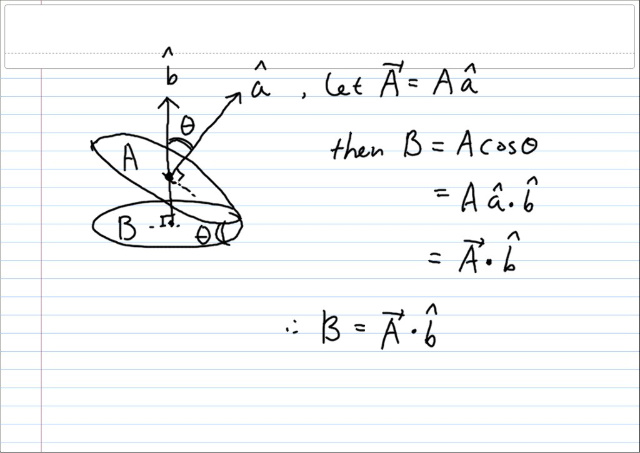
우선 면적을 사영하는 것부터 살펴보면...
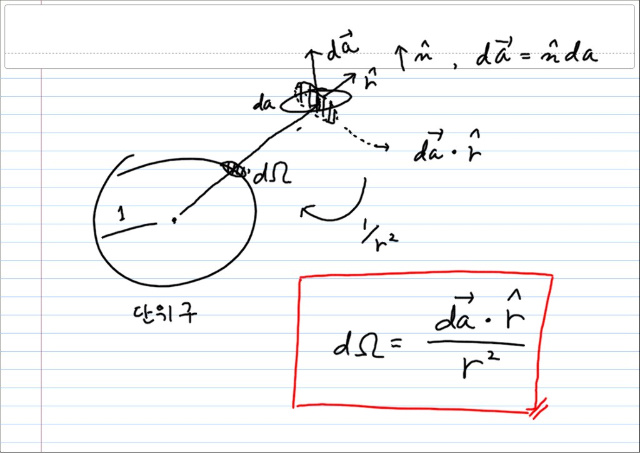
이제, 미소 입체각을 보면...
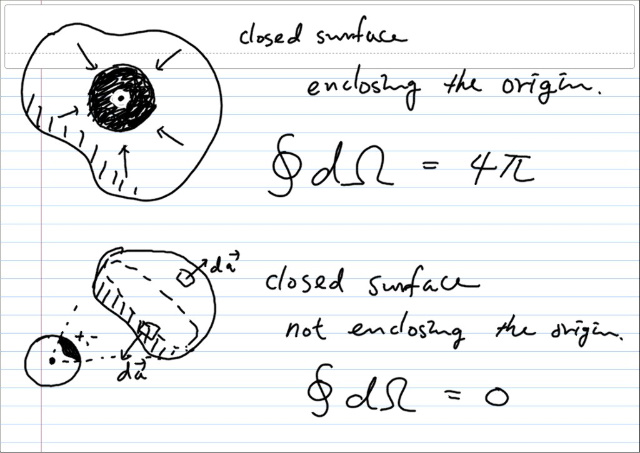
이것은 원점을 중심으로하는 구면전체에 대해 적분하면 당연히 4π 가 될 것이다. 사실은 그 모양에 상관없이 원점을 포함하는 폐곡면에 대해서도 마찬가지 일것이다. 반면 원점을 포함하지 않는 폐곡면에 대해서는 r 단위벡터와 da벡터의 내적이 +,- 상쇄가 되어 0 이 될 것이다.
이것은 때때로, 중적분을 간단하게 처리하는데 도움을 준다.
예를 들면 대충 이런식이다...