[역학] 왜 우리는 달의 한면만 보게 될까? ( Tidal Locking )
Physics/Math./Mech./Gen. Relativity2008. 6. 1. 20:37 |달의 한면만 보게 되는 현상에 대해 중학교때 달의 자전 주기와 공전 주기가 같아서 그렇다고 배웠을 것이다. 그런데, 어떻게 공전주기와 자전주기가 같을수가 있을까? 하루에 0.001 도씩만 차이가 나도, 500년이면 뒷면을 보게 될텐데 말이다. 이러한 질문은 당연한 것이고, 이러한 질문이 곧 과학적 태도이며 동시에 과학교육의 본질인 것이다.
아무튼, 그때 물상 선생님한테, 그 이유에 대해 물었을때 돌아온 답은 역시 교과서 그대로였다. 달의 자전주기와 공전주기가 같아서 라고... 나는 즉각, 어떻게 그것이 가능하냐고 물었는데, 역시나 되돌아온 대답은 "관찰의 결과" 그렇기 때문이라는 것이다.
여기서 응당 이어져야 할 의문은 " 그럼 어떻게 그것은 지속가능한 것입니까? " 라고 할 수 있겠다. 왜냐하면, 달의 수많은 크레이터 들이 보여주듯이, 운석의 충돌이나 어떠한 우주적인 사건에 의해 달의 회전에는 변화가 생길수 있기 때문이다. 그렇게 따져 물었어야 했는데, 그땐 그냥 돌아섰다. 아무튼 끝까지 미심쩍어서 쉬이 발길이 돌아서지 못하던 때에 돌아온 대답은 의외로 종교적이었다.
지구가 그만큼 특별한거라고... -_-;;;
그.러.나.
현재 역학을 공부하다가 tidal force 에 대해 공부하게 되면서 알게 된건데... 지구와 달 만의 현상이 아니란거다. -_- 아주 보편적인 현상이며 오랜 시간이 지나면 이벤추얼리 대부분의 돌고도는 위성 행성 별 등이 서로 같은 면만 보게 된다. 이를 타이들 락킹 이라고 한다.
아래 위키에서 퍼온 설명인데, 보면 알겠지만, locked 된 애들 무지 많다. -_- 달만 그런게 아니다. 그리고 아직 locked 안된 애들도, 대체로 고정이 되는 중인거다.
자세한 설명은 아래에 나와 있다. 궁금한 사람은 꼭 자세히 읽어보도록 하자. 어느정도 이해할려면 적어도 종이와 연필을 들고 그림 몇장 정도는 그려야 할 것이다. 다음에 기회가 되면 그림과 함께 풀어서 설명을 해보도록 하겠다.
Tidal Locking
Tidal locking occurs when the gravitational gradient makes one side of an astronomical body always face another
; for example, one side of the Earth's Moon always faces the Earth.
A tidally locked body takes just as long to rotate around its own axis as it does to revolve around its partner. This synchronous rotation causes one hemisphere constantly to face the partner body.
Usually, only the satellite becomes tidally locked around the larger planet, but if the difference in mass between the two bodies and their physical separation is small, both may become tidally locked to the other, as is the case between Pluto and Charon. This effect is employed to stabilize some artificial satellites.
Mechanism of Tidal Locking
The change in rotation rate necessary to tidally lock a body B to a larger body A is caused by the torque applied by A's gravity on bulges it has induced on B by tidal forces.
Tidal bulges
A's gravity produces a tidal force on B which distorts its gravitational equilibrium shape slightly so that it becomes stretched along the axis oriented toward A, and conversely, is slightly compressed in the two perpendicular directions.
These distortions are known as tidal bulges.
When B is not yet tidally locked, the bulges travel over its surface, with one of the two "high" tidal bulges traveling close to the point where body A is overhead.
For large astronomical bodies which are near-spherical due to self-gravitation, the tidal distortion produces a slightly prolate spheroid or ellipsoid.
Smaller bodies also experience distortion, but this distortion is less regular.
Bulge dragging
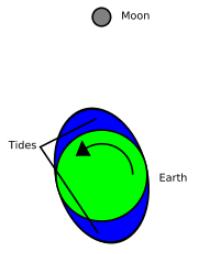
The material of B exerts resistance to this periodic reshaping caused by the tidal force.
In effect, some time is required to reshape B to the gravitational equilibrium shape, by which time the forming bulges have already been carried some distance away from the A-B axis by B's rotation.
Seen from a vantage point in space, the points of maximum bulge extension are displaced from the axis oriented towards A.
If B's rotation period is shorter than its orbital period, the bulges are carried forward of the axis oriented towards A in the direction of rotation, whereas if B's orbital period is shorter the bulges lag behind instead.
Resulting torque
Since the bulges are now displaced from the A-B axis, A's gravitational pull on the mass in them exerts a torque on B.
The torque on the A-facing bulge acts to bring B's rotation in line with its orbital period, while the "back" bulge which faces away from A acts in the opposite sense.
However, the bulge on the A-facing side is closer to A than the back bulge by a distance of approximately B's diameter, and so experiences a slightly stronger gravitational force and torque.
The net resulting torque from both bulges, then, is always in the direction which acts to synchronize B's rotation with its orbital period, leading eventually to tidal locking.
Orbital changes
The angular momentum of the whole A-B system is conserved in this process, so that when B slows down and loses rotational angular momentum, its orbital angular momentum is boosted by a similar amount (there are also some smaller effects on A's rotation).
This results in a raising of B's orbit about A in tandem with its rotational slowdown.
For the other case where B starts off rotating too slowly, tidal locking both speeds up its rotation, and lowers its orbit.
Locking of the larger body
The tidal locking effect is also experienced by the larger body A, but at a slower rate because B's gravitational effect is weaker due to B's smaller size.
For example, the Earth's rotation is gradually slowing down because of the Moon, by an amount that becomes noticeable over geological time in some fossils.
For similar sized bodies the effect may be of comparable size for both, and both may become tidally locked to each other.
The dwarf planet Pluto and its satellite Charon are good examples of this— Charon is only visible from one hemisphere of Pluto and vice versa.
Tidal acceleration
Tidal acceleration is an effect of the tidal forces between an orbiting natural satellite (i.e. a moon), and the planet (called the primary) that it orbits.
It causes a gradual recession of a satellite in a prograde orbit away from the primary, and a corresponding slowdown of the primary's rotation.
The process eventually leads to tidal locking of first the smaller, and later the larger body.
The Earth-Moon system is the best studied case.
The similar process of tidal deceleration occurs for satellites that have an orbital period that is shorter than the primary's rotation period, or that orbit in a retrograde direction.
Effects of moon's gravity
Because the Moon's mass is a considerable fraction of that of the Earth (about 1:81), the two bodies can be regarded as a double planet system, rather than as a planet with a satellite.
The plane of the Moon's orbit around the Earth lies close to the plane of the Earth's orbit around the Sun (the ecliptic), rather than in the plane perpendicular to the axis of rotation of the Earth (the equator) as is usually the case with planetary satellites.
The mass of the Moon is sufficiently large and it is sufficiently close to raise tides in the Earth:
the matter of the Earth, in particular the water of the oceans, bulges out along both ends of an axis passing through the centers of the Earth and Moon.
The average tidal bulge closely follows the Moon in its orbit, and the Earth rotates under this tidal bulge in just over a day.
However, the rotation drags the position of the tidal bulge ahead of the position directly under the Moon.
As a consequence, there exists a substantial amount of mass in the bulge that is offset from the line through the centers of the Earth and Moon.
Because of this offset, a portion of the gravitational pull between Earth's tidal bulges and the Moon is perpendicular to the Earth-Moon line, i.e. there exists a torque between the Earth and the Moon.
This accelerates the Moon in its orbit, and decelerates the rotation of the Earth.
So the result is that the mean solar day, which is nominally 86400 seconds long, is actually getting longer when measured in SI seconds with stable atomic clocks.
The small difference accumulates every day, which leads to an increasing difference between our clock time (Universal Time) on the one hand, and Atomic Time and Ephemeris Time on the other hand: see ΔT.
This makes it necessary to insert a leap second at irregular intervals.
If other effects were ignored, tidal acceleration would continue until the rotational period of the Earth matched the orbital period of the Moon.
At that time, the Moon would always be overhead of a single fixed place on Earth.
Such a situation already exists in the Pluto-Charon system.
However, the slowdown of the Earth's rotation is not occurring fast enough for the rotation to lengthen to a month before other effects make this irrelevant:
About 2.1 billion years from now, the continual increase of the Sun's radiation will cause the Earth's oceans to boil away, removing the bulk of the tidal friction and acceleration.
Even without this, the slowdown to a month-long day would still not have been completed by 4.5 billion years from now when the Sun will evolve into a red giant and likely destroy both the Earth and Moon.
Tidal acceleration is one of the few examples in the dynamics of the solar system of a so-called secular perturbation of an orbit, i.e. a perturbation that continuously increases with time and is not periodic.
Up to a high order of approximation, mutual gravitational perturbations between major or minor planets only cause periodic variations in their orbits, that is, parameters oscillate between maximum and minimum values.
The tidal effect gives rise to a quadratic term in the equations, which leads to unbounded growth.
In the mathematical theories of the planetary orbits that form the basis of ephemerides, quadratic and higher order secular terms do occur, but these are mostly Taylor expansions of very long time periodic terms.
The reason that tidal effects are different is that unlike distant gravitational perturbations, friction is an essential part of tidal acceleration, and leads to permanent loss of energy in the form of heat.
Angular momentum and energy
The gravitational torque between the Moon and the tidal bulge of the Earth causes the Moon to be accelerated in its orbit, and the Earth to be decelerated in its rotation.
As in any physical process, total energy and angular momentum are conserved.
Effectively, energy and angular momentum are transferred from the rotation of the Earth to the orbital motion of the Moon.
The Moon moves farther away from the Earth, so its potential energy (in the Earth's gravity well) increases.
It stays in orbit, and from Kepler's 3rd law it follows that its velocity actually decreases, so the tidal acceleration of the Moon causes an apparent deceleration of its motion across the celestial sphere.
Although its kinetic energy decreases, its potential energy increases by a larger amount.
The Moon's orbital angular momentum also increases.
The rotational angular momentum of the Earth decreases and consequently the length of the day increases.
The net tide raised on Earth by the Moon is dragged ahead of the Moon by Earth's much faster rotation.
Tidal friction is required to drag and maintain the bulge ahead of the Moon, and it dissipates the excess energy of the exchange of rotational and orbital energy between the Earth and Moon as heat.
If the friction and heat dissipation were not present, the Moon's gravitational force on the tidal bulge would rapidly (within two days) bring the tide back into synchronization with the Moon, and the Moon would no longer recede.
Most of the dissipation occurs in a turbulent bottom boundary layer in shallow seas such as the European shelf around the British Isles, the Patagonian shelf off Argentina, and the Bering Sea.
A tidal bulge (called an equilibrium tide) does not really exist on Earth because the continents break up the tide when they pass under the Moon.
Oceanic tides actually rotate around each ocean basin as vast gyres around several amphidromic points where no tide exists.
The Moon pulls on each individual undulation as Earth rotates—some undulations are ahead of the Moon, others are behind it, while still others are on either side.
The equilibrium tide in the shape of a prolate spheroid that actually does exist for the Moon to pull on is the net result of integrating the actual undulations over all the world's oceans.
Earth's net equilibrium tide has an amplitude of only 3.23 cm, which is totally swamped by oceanic tides that can exceed one metre.
Historical evidence
This mechanism has been working for 4.5 billion years, since oceans first formed on the Earth.
There is geological and paleontological evidence that the Earth rotated faster and that the Moon was closer to the Earth in the remote past.
Tidal rhythmites are alternating layers of sand and silt laid down offshore from estuaries having great tidal flows.
Daily, monthly and seasonal cycles can be found in the deposits.
This geological record is consistent with these conditions 620 million years ago:
the day was 21.9±0.4 hours, and there were 13.1±0.1 synodic months/year and 400±7 solar days/year.
The length of the year has remained virtually unchanged during this period because no evidence exists that the constant of gravitation has changed.
The average recession rate of the Moon between then and now has been 2.17±0.31 cm/year, which is about half the present rate.
Quantitative description of the Earth-Moon case
The motion of the Moon can be followed with an accuracy of a few centimeters by lunar laser ranging (LLR).
Laser pulses are bounced off mirrors on the surface of the moon, emplaced during the Apollo missions of 1969 to 1972 and by Lunokhod 2 in 1973.
Measuring the return time of the pulse yields a very accurate measure of the distance.
These measurements are fitted to the equations of motion.
This yields numerical values for the parameters, among others the secular acceleration.
From the period 1969–2001, the result is:
+3.84 ± 0.07 m/cy in distance
This is consistent with results from satellite laser ranging (SLR). This is a similar technique applied to artificial satellites orbiting the Earth.
This yields an accurate model for the gravitational field of the Earth, including that of the tides.
This can be used to predict its effect on the motion of the Moon, which yield very similar results.
Finally, ancient observations of solar eclipses give a fairly accurate position for the Moon at that moment.
Studies of these give results consistent with the value quoted above.
The other consequence of the tidal acceleration is the deceleration of the rotation of the Earth.
The rotation of the Earth is somewhat erratic on all time scales (from hours to centuries) due to various causes.
The small tidal effect can not be observed in a short period but the cumulative effect of the Earth's actual daily rotation occurring in less than 24 hours as measured on a stable clock (ephemeris time, atomic time) even a few milliseconds every day, becomes readily noticeable in a few centuries.
Since some event in the remote past, more days and hours have passed (as measured in full rotations of the Earth) (Universal Time) than as measured with stable clocks calibrated to the present, longer length of the day (ephemeris time).
This is known as ΔT. Recent values can be obtained from the International Earth Rotation and Reference Systems Service (IERS).
A table of the actual length of the day in the past few centuries is also available.
From the observed acceleration of the Moon, the corresponding change in the length of the day can be computed:
+2.3 ms/cy
However, from historical records over the past 2700 years the following average value is found:
+1.70 ± 0.05 ms/cy
The corresponding cumulative value is a parabola having a coefficient of T² (time in centuries squared) of:
ΔT = +31 s/cy²
Counter to the tidal deceleration of the Earth, there is a mechanism that is in fact accelerating the rotation.
The Earth is not a sphere, but rather an ellipsoid that is flattened at the poles.
SLR has shown that this flattening is decreasing.
The explanation is, that during the ice age large masses of ice collected at the poles, and depressed the underlying rocks.
The ice mass started disappearing over 10000 years ago, but the Earth's crust is still not in hydrostatic equilibrium and is still rebounding (the relaxation time is estimated to be about 4000 years).
As a consequence, the polar diameter of the Earth increases, and since the mass and density remain the same, the volume remains the same;
therefore the equatorial diameter is decreasing.
As a consequence, mass moves closer to the rotation axis of the Earth.
This means that its moment of inertia is decreasing.
Because its total angular momentum remains the same during this process, the rotation rate increases.
This is the well-known effect of a spinning figure skater who spins ever faster as she retracts her arms.
From the observed change in the moment of inertia the acceleration of rotation can be computed:
the average value over the historical period must have been about −0.6 ms/cy .
This largely explains the historical observations.
Rotation-Orbit resonance
Finally, in some cases where the orbit is eccentric and the tidal effect is relatively weak, the smaller body may end up in an orbital resonance, rather than tidally locked.
Here the ratio of rotation period to orbital period is some well-defined fraction different from 1:1.
A well known case is the rotation of Mercury—locked to its orbit around the Sun in a 3:2 resonance.
Final configuration
There is a tendency for a moon to orient itself in the lowest energy configuration, with the heavy side facing the planet.
Irregularly shaped bodies will align their long axis to point towards the planet.
Both cases are analogous to how a rounded floating object will orient itself with its heavy end downwards.
In many cases this planet-facing hemisphere is visibly different from the rest of the moon's surface.
The orientation of the Earth's moon might be related to this process.
The lunar maria are composed of basalt, which is heavier than the surrounding highland crust, and were formed on the side of the moon on which the crust is markedly thinner.
The Earth-facing hemisphere contains all the large maria.
The simple picture of the moon stabilising with its heavy side towards the Earth is incorrect, however, because the tidal locking occurred over a very short timescale of a thousand years or less, while the maria formed much later.
Earth's Moon
The Moon's rotation and orbital periods are both just under 4 weeks, so no matter when the Moon is observed from the Earth the same hemisphere of the Moon is always seen.
The far side of the Moon was not seen in its entirety until 1959, when photographs were transmitted from the Soviet spacecraft Luna 3.
Despite the Moon's rotational and orbital periods being exactly locked, we may actually observe about 59% of the moon's total surface with repeated observations from earth due to the phenomena of librations and parallax.
Librations are primarily caused by the Moon's varying orbital speed due to the eccentricity of its orbit: this allows us to see up to about 6° more along its perimeter.
Parallax is a geometric effect : at the surface of the Earth we are offset from the line through the centers of Earth and Moon, and because of this we can observe a bit (about 1°) more around the side of the Moon when it is on our local horizon.
Moons
Most significant moons in the Solar System are tidally locked with their primaries, since they orbit very closely and tidal force increases rapidly (as a cubic) with decreasing distance.
Notable exceptions are the irregular outer satellites of the gas giant planets, which orbit much further away than the large well-known moons.
Pluto and Charon are an extreme example of a tidal lock. Charon is a relatively large moon in comparison to its primary and also has a very close orbit. This has made Pluto also tidally locked to Charon.
In effect, these two celestial bodies revolve around each other (their mass center lies outside of Pluto) as if joined with a rod connecting two opposite points on their surfaces.
The tidal locking situation for asteroid moons is largely unknown, but closely-orbiting binaries are expected to be tidally locked, as well as, obviously, contact binaries.
Planets
Until radar observations in 1965 proved otherwise, it was thought that Mercury was tidally locked with the Sun.
Instead, it turned out that Mercury has a 3:2 spin-orbit resonance, rotating three times for every two revolutions around the Sun
; the eccentricity of Mercury's orbit makes this resonance stable.
The original reason astronomers thought it was tidally locked was because whenever Mercury was best placed for observation, it was always at the same point in its 3:2 resonance, so showing the same face, which would be also the case if it were totally locked.
A curious aspect of Venus' orbit and rotation periods is that the 583.92-day interval between successive close approaches to the Earth is almost exactly equal to 5 Venusian solar days (precisely, 5.001444 of these), making approximately the same face visible from Earth at each close approach.
Whether this relationship arose by chance or is the result of some kind of tidal locking with the Earth is unknown.
Stars
Close binary stars throughout the universe are expected to be tidally locked with each other, and extrasolar planets that have been found to orbit their primaries extremely closely are also thought to be tidally locked to them.
An unusual example, confirmed by MOST, is Tau Boötis, a star tidally locked by a planet. The tidal locking is almost certainly mutual.


As can be seen, even knowing the size and density of the satellite leaves many parameters that must be estimated (especially w, Q, and , μ ), so that any calculated locking times obtained are expected to be inaccurate, to even factors of ten.
Further, during the tidal locking phase the orbital radius a may have been significantly different from that observed nowadays due to subsequent tidal acceleration, and the locking time is extremely sensitive to this value.
Since the uncertainty is so high, the above formulas can be simplified to give a somewhat less cumbersome one.
By assuming that the satellite is spherical, k_2 << 1 , Q = 100, and it is sensible to guess one revolution every 12 hours in the initial non-locked state (most asteroids have rotational periods between about 2 hours and about 2 days)
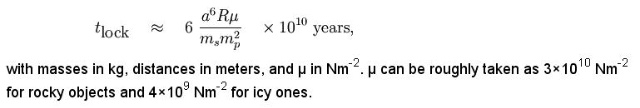
Note the extremely strong dependence on orbital radius a.
For the locking of a primary body to its moon as in the case of Pluto, satellite and primary body parameters can be interchanged.
One conclusion is that other things being equal (such as Q and μ), a large moon will lock faster than a smaller moon at the same orbital radius from the planet because m_s , grows much faster with satellite radius than R.
A possible example of this is in the Saturn system, where Hyperion is not tidally locked, while the larger Iapetus, which orbits at a greater distance, is.
This is not clear cut because Hyperion also experiences strong driving from the nearby Titan, which forces its rotation to be chaotic.
List of known tidally locked bodies
<< Solar System >>
Locked to the Sun
* Mercury (in a 3:2 rotation:orbit resonance)
Locked to the Earth
* Moon
Locked to Mars
* Phobos
* Deimos
Locked to Jupiter
* Metis
* Adrastea
* Amalthea
* Thebe
* Io
* Europa
* Ganymede
* Callisto
Locked to Saturn
* Pan
* Atlas
* Prometheus
* Pandora
* Epimetheus
* Janus
* Mimas
* Enceladus
* Telesto
* Tethys
* Calypso
* Dione
* Rhea
* Titan
* Iapetus
Locked to Uranus
* Miranda
* Ariel
* Umbriel
* Titania
Locked to Neptune
* Proteus
* Triton
Locked to Pluto
* Charon (Pluto being itself locked to Charon)
<< Extra-solar >>
* Tau Boötis is known to be locked to the close-orbiting giant planet Tau Boötis Ab[citation needed]
Bodies likely to be locked
<< Solar System >>
Based on comparison between the likely time needed to lock a body to its primary, and the time it has been in its present orbit (comparable with the age of the Solar System for most planetary moons), a number of moons are thought to be locked.
However their rotations are not known or not known enough.
These are:
Probably locked to Saturn
* Daphnis
* S/2004 S 6
* S/2004 S 4
* S/2004 S 3
* Methone
* Pallene
* Helene
* Polydeuces
Probably locked to Uranus
* Cordelia
* Ophelia
* Bianca
* Cressida
* Desdemona
* Juliet
* Portia
* Rosalind
* Cupid
* Belinda
* Perdita
* Puck
* Mab
* Oberon
Probably locked to Neptune
* Naiad
* Thalassa
* Despina
* Galatea
* Larissa
Probably locked to other dwarf planets and minor planets
Numerous asteroid and TNO moons are expected to be locked to their primaries. However, in the absence of direct observation reliable candidates are difficult to verify. While locking timescales can be estimated, the age of the primary+satellite system is difficult to gauge; most are thought to be the results of collisions in the last few hundred million years.
<< Extra-solar >>
* Gliese 581 c may be tidally locked to its parent star Gliese 581.
아무튼, 그때 물상 선생님한테, 그 이유에 대해 물었을때 돌아온 답은 역시 교과서 그대로였다. 달의 자전주기와 공전주기가 같아서 라고... 나는 즉각, 어떻게 그것이 가능하냐고 물었는데, 역시나 되돌아온 대답은 "관찰의 결과" 그렇기 때문이라는 것이다.
여기서 응당 이어져야 할 의문은 " 그럼 어떻게 그것은 지속가능한 것입니까? " 라고 할 수 있겠다. 왜냐하면, 달의 수많은 크레이터 들이 보여주듯이, 운석의 충돌이나 어떠한 우주적인 사건에 의해 달의 회전에는 변화가 생길수 있기 때문이다. 그렇게 따져 물었어야 했는데, 그땐 그냥 돌아섰다. 아무튼 끝까지 미심쩍어서 쉬이 발길이 돌아서지 못하던 때에 돌아온 대답은 의외로 종교적이었다.
지구가 그만큼 특별한거라고... -_-;;;
그.러.나.
현재 역학을 공부하다가 tidal force 에 대해 공부하게 되면서 알게 된건데... 지구와 달 만의 현상이 아니란거다. -_- 아주 보편적인 현상이며 오랜 시간이 지나면 이벤추얼리 대부분의 돌고도는 위성 행성 별 등이 서로 같은 면만 보게 된다. 이를 타이들 락킹 이라고 한다.
아래 위키에서 퍼온 설명인데, 보면 알겠지만, locked 된 애들 무지 많다. -_- 달만 그런게 아니다. 그리고 아직 locked 안된 애들도, 대체로 고정이 되는 중인거다.
자세한 설명은 아래에 나와 있다. 궁금한 사람은 꼭 자세히 읽어보도록 하자. 어느정도 이해할려면 적어도 종이와 연필을 들고 그림 몇장 정도는 그려야 할 것이다. 다음에 기회가 되면 그림과 함께 풀어서 설명을 해보도록 하겠다.
Tidal Locking
Tidal locking occurs when the gravitational gradient makes one side of an astronomical body always face another
; for example, one side of the Earth's Moon always faces the Earth.
A tidally locked body takes just as long to rotate around its own axis as it does to revolve around its partner. This synchronous rotation causes one hemisphere constantly to face the partner body.
Usually, only the satellite becomes tidally locked around the larger planet, but if the difference in mass between the two bodies and their physical separation is small, both may become tidally locked to the other, as is the case between Pluto and Charon. This effect is employed to stabilize some artificial satellites.
Mechanism of Tidal Locking
The change in rotation rate necessary to tidally lock a body B to a larger body A is caused by the torque applied by A's gravity on bulges it has induced on B by tidal forces.
Tidal bulges
A's gravity produces a tidal force on B which distorts its gravitational equilibrium shape slightly so that it becomes stretched along the axis oriented toward A, and conversely, is slightly compressed in the two perpendicular directions.
These distortions are known as tidal bulges.
When B is not yet tidally locked, the bulges travel over its surface, with one of the two "high" tidal bulges traveling close to the point where body A is overhead.
For large astronomical bodies which are near-spherical due to self-gravitation, the tidal distortion produces a slightly prolate spheroid or ellipsoid.
Smaller bodies also experience distortion, but this distortion is less regular.
Bulge dragging

The material of B exerts resistance to this periodic reshaping caused by the tidal force.
In effect, some time is required to reshape B to the gravitational equilibrium shape, by which time the forming bulges have already been carried some distance away from the A-B axis by B's rotation.
Seen from a vantage point in space, the points of maximum bulge extension are displaced from the axis oriented towards A.
If B's rotation period is shorter than its orbital period, the bulges are carried forward of the axis oriented towards A in the direction of rotation, whereas if B's orbital period is shorter the bulges lag behind instead.
Resulting torque
Since the bulges are now displaced from the A-B axis, A's gravitational pull on the mass in them exerts a torque on B.
The torque on the A-facing bulge acts to bring B's rotation in line with its orbital period, while the "back" bulge which faces away from A acts in the opposite sense.
However, the bulge on the A-facing side is closer to A than the back bulge by a distance of approximately B's diameter, and so experiences a slightly stronger gravitational force and torque.
The net resulting torque from both bulges, then, is always in the direction which acts to synchronize B's rotation with its orbital period, leading eventually to tidal locking.
Orbital changes
The angular momentum of the whole A-B system is conserved in this process, so that when B slows down and loses rotational angular momentum, its orbital angular momentum is boosted by a similar amount (there are also some smaller effects on A's rotation).
This results in a raising of B's orbit about A in tandem with its rotational slowdown.
For the other case where B starts off rotating too slowly, tidal locking both speeds up its rotation, and lowers its orbit.
Locking of the larger body
The tidal locking effect is also experienced by the larger body A, but at a slower rate because B's gravitational effect is weaker due to B's smaller size.
For example, the Earth's rotation is gradually slowing down because of the Moon, by an amount that becomes noticeable over geological time in some fossils.
For similar sized bodies the effect may be of comparable size for both, and both may become tidally locked to each other.
The dwarf planet Pluto and its satellite Charon are good examples of this— Charon is only visible from one hemisphere of Pluto and vice versa.
Tidal acceleration
Tidal acceleration is an effect of the tidal forces between an orbiting natural satellite (i.e. a moon), and the planet (called the primary) that it orbits.
It causes a gradual recession of a satellite in a prograde orbit away from the primary, and a corresponding slowdown of the primary's rotation.
The process eventually leads to tidal locking of first the smaller, and later the larger body.
The Earth-Moon system is the best studied case.
The similar process of tidal deceleration occurs for satellites that have an orbital period that is shorter than the primary's rotation period, or that orbit in a retrograde direction.
Effects of moon's gravity
Because the Moon's mass is a considerable fraction of that of the Earth (about 1:81), the two bodies can be regarded as a double planet system, rather than as a planet with a satellite.
The plane of the Moon's orbit around the Earth lies close to the plane of the Earth's orbit around the Sun (the ecliptic), rather than in the plane perpendicular to the axis of rotation of the Earth (the equator) as is usually the case with planetary satellites.
The mass of the Moon is sufficiently large and it is sufficiently close to raise tides in the Earth:
the matter of the Earth, in particular the water of the oceans, bulges out along both ends of an axis passing through the centers of the Earth and Moon.
The average tidal bulge closely follows the Moon in its orbit, and the Earth rotates under this tidal bulge in just over a day.
However, the rotation drags the position of the tidal bulge ahead of the position directly under the Moon.
As a consequence, there exists a substantial amount of mass in the bulge that is offset from the line through the centers of the Earth and Moon.
Because of this offset, a portion of the gravitational pull between Earth's tidal bulges and the Moon is perpendicular to the Earth-Moon line, i.e. there exists a torque between the Earth and the Moon.
This accelerates the Moon in its orbit, and decelerates the rotation of the Earth.
So the result is that the mean solar day, which is nominally 86400 seconds long, is actually getting longer when measured in SI seconds with stable atomic clocks.
The small difference accumulates every day, which leads to an increasing difference between our clock time (Universal Time) on the one hand, and Atomic Time and Ephemeris Time on the other hand: see ΔT.
This makes it necessary to insert a leap second at irregular intervals.
If other effects were ignored, tidal acceleration would continue until the rotational period of the Earth matched the orbital period of the Moon.
At that time, the Moon would always be overhead of a single fixed place on Earth.
Such a situation already exists in the Pluto-Charon system.
However, the slowdown of the Earth's rotation is not occurring fast enough for the rotation to lengthen to a month before other effects make this irrelevant:
About 2.1 billion years from now, the continual increase of the Sun's radiation will cause the Earth's oceans to boil away, removing the bulk of the tidal friction and acceleration.
Even without this, the slowdown to a month-long day would still not have been completed by 4.5 billion years from now when the Sun will evolve into a red giant and likely destroy both the Earth and Moon.
Tidal acceleration is one of the few examples in the dynamics of the solar system of a so-called secular perturbation of an orbit, i.e. a perturbation that continuously increases with time and is not periodic.
Up to a high order of approximation, mutual gravitational perturbations between major or minor planets only cause periodic variations in their orbits, that is, parameters oscillate between maximum and minimum values.
The tidal effect gives rise to a quadratic term in the equations, which leads to unbounded growth.
In the mathematical theories of the planetary orbits that form the basis of ephemerides, quadratic and higher order secular terms do occur, but these are mostly Taylor expansions of very long time periodic terms.
The reason that tidal effects are different is that unlike distant gravitational perturbations, friction is an essential part of tidal acceleration, and leads to permanent loss of energy in the form of heat.
Angular momentum and energy
The gravitational torque between the Moon and the tidal bulge of the Earth causes the Moon to be accelerated in its orbit, and the Earth to be decelerated in its rotation.
As in any physical process, total energy and angular momentum are conserved.
Effectively, energy and angular momentum are transferred from the rotation of the Earth to the orbital motion of the Moon.
The Moon moves farther away from the Earth, so its potential energy (in the Earth's gravity well) increases.
It stays in orbit, and from Kepler's 3rd law it follows that its velocity actually decreases, so the tidal acceleration of the Moon causes an apparent deceleration of its motion across the celestial sphere.
Although its kinetic energy decreases, its potential energy increases by a larger amount.
The Moon's orbital angular momentum also increases.
The rotational angular momentum of the Earth decreases and consequently the length of the day increases.
The net tide raised on Earth by the Moon is dragged ahead of the Moon by Earth's much faster rotation.
Tidal friction is required to drag and maintain the bulge ahead of the Moon, and it dissipates the excess energy of the exchange of rotational and orbital energy between the Earth and Moon as heat.
If the friction and heat dissipation were not present, the Moon's gravitational force on the tidal bulge would rapidly (within two days) bring the tide back into synchronization with the Moon, and the Moon would no longer recede.
Most of the dissipation occurs in a turbulent bottom boundary layer in shallow seas such as the European shelf around the British Isles, the Patagonian shelf off Argentina, and the Bering Sea.
A tidal bulge (called an equilibrium tide) does not really exist on Earth because the continents break up the tide when they pass under the Moon.
Oceanic tides actually rotate around each ocean basin as vast gyres around several amphidromic points where no tide exists.
The Moon pulls on each individual undulation as Earth rotates—some undulations are ahead of the Moon, others are behind it, while still others are on either side.
The equilibrium tide in the shape of a prolate spheroid that actually does exist for the Moon to pull on is the net result of integrating the actual undulations over all the world's oceans.
Earth's net equilibrium tide has an amplitude of only 3.23 cm, which is totally swamped by oceanic tides that can exceed one metre.
Historical evidence
This mechanism has been working for 4.5 billion years, since oceans first formed on the Earth.
There is geological and paleontological evidence that the Earth rotated faster and that the Moon was closer to the Earth in the remote past.
Tidal rhythmites are alternating layers of sand and silt laid down offshore from estuaries having great tidal flows.
Daily, monthly and seasonal cycles can be found in the deposits.
This geological record is consistent with these conditions 620 million years ago:
the day was 21.9±0.4 hours, and there were 13.1±0.1 synodic months/year and 400±7 solar days/year.
The length of the year has remained virtually unchanged during this period because no evidence exists that the constant of gravitation has changed.
The average recession rate of the Moon between then and now has been 2.17±0.31 cm/year, which is about half the present rate.
Quantitative description of the Earth-Moon case
The motion of the Moon can be followed with an accuracy of a few centimeters by lunar laser ranging (LLR).
Laser pulses are bounced off mirrors on the surface of the moon, emplaced during the Apollo missions of 1969 to 1972 and by Lunokhod 2 in 1973.
Measuring the return time of the pulse yields a very accurate measure of the distance.
These measurements are fitted to the equations of motion.
This yields numerical values for the parameters, among others the secular acceleration.
From the period 1969–2001, the result is:
+3.84 ± 0.07 m/cy in distance
This is consistent with results from satellite laser ranging (SLR). This is a similar technique applied to artificial satellites orbiting the Earth.
This yields an accurate model for the gravitational field of the Earth, including that of the tides.
This can be used to predict its effect on the motion of the Moon, which yield very similar results.
Finally, ancient observations of solar eclipses give a fairly accurate position for the Moon at that moment.
Studies of these give results consistent with the value quoted above.
The other consequence of the tidal acceleration is the deceleration of the rotation of the Earth.
The rotation of the Earth is somewhat erratic on all time scales (from hours to centuries) due to various causes.
The small tidal effect can not be observed in a short period but the cumulative effect of the Earth's actual daily rotation occurring in less than 24 hours as measured on a stable clock (ephemeris time, atomic time) even a few milliseconds every day, becomes readily noticeable in a few centuries.
Since some event in the remote past, more days and hours have passed (as measured in full rotations of the Earth) (Universal Time) than as measured with stable clocks calibrated to the present, longer length of the day (ephemeris time).
This is known as ΔT. Recent values can be obtained from the International Earth Rotation and Reference Systems Service (IERS).
A table of the actual length of the day in the past few centuries is also available.
From the observed acceleration of the Moon, the corresponding change in the length of the day can be computed:
+2.3 ms/cy
However, from historical records over the past 2700 years the following average value is found:
+1.70 ± 0.05 ms/cy
The corresponding cumulative value is a parabola having a coefficient of T² (time in centuries squared) of:
ΔT = +31 s/cy²
Counter to the tidal deceleration of the Earth, there is a mechanism that is in fact accelerating the rotation.
The Earth is not a sphere, but rather an ellipsoid that is flattened at the poles.
SLR has shown that this flattening is decreasing.
The explanation is, that during the ice age large masses of ice collected at the poles, and depressed the underlying rocks.
The ice mass started disappearing over 10000 years ago, but the Earth's crust is still not in hydrostatic equilibrium and is still rebounding (the relaxation time is estimated to be about 4000 years).
As a consequence, the polar diameter of the Earth increases, and since the mass and density remain the same, the volume remains the same;
therefore the equatorial diameter is decreasing.
As a consequence, mass moves closer to the rotation axis of the Earth.
This means that its moment of inertia is decreasing.
Because its total angular momentum remains the same during this process, the rotation rate increases.
This is the well-known effect of a spinning figure skater who spins ever faster as she retracts her arms.
From the observed change in the moment of inertia the acceleration of rotation can be computed:
the average value over the historical period must have been about −0.6 ms/cy .
This largely explains the historical observations.
Rotation-Orbit resonance
Finally, in some cases where the orbit is eccentric and the tidal effect is relatively weak, the smaller body may end up in an orbital resonance, rather than tidally locked.
Here the ratio of rotation period to orbital period is some well-defined fraction different from 1:1.
A well known case is the rotation of Mercury—locked to its orbit around the Sun in a 3:2 resonance.
Final configuration
There is a tendency for a moon to orient itself in the lowest energy configuration, with the heavy side facing the planet.
Irregularly shaped bodies will align their long axis to point towards the planet.
Both cases are analogous to how a rounded floating object will orient itself with its heavy end downwards.
In many cases this planet-facing hemisphere is visibly different from the rest of the moon's surface.
The orientation of the Earth's moon might be related to this process.
The lunar maria are composed of basalt, which is heavier than the surrounding highland crust, and were formed on the side of the moon on which the crust is markedly thinner.
The Earth-facing hemisphere contains all the large maria.
The simple picture of the moon stabilising with its heavy side towards the Earth is incorrect, however, because the tidal locking occurred over a very short timescale of a thousand years or less, while the maria formed much later.
Earth's Moon
The Moon's rotation and orbital periods are both just under 4 weeks, so no matter when the Moon is observed from the Earth the same hemisphere of the Moon is always seen.
The far side of the Moon was not seen in its entirety until 1959, when photographs were transmitted from the Soviet spacecraft Luna 3.
Despite the Moon's rotational and orbital periods being exactly locked, we may actually observe about 59% of the moon's total surface with repeated observations from earth due to the phenomena of librations and parallax.
Librations are primarily caused by the Moon's varying orbital speed due to the eccentricity of its orbit: this allows us to see up to about 6° more along its perimeter.
Parallax is a geometric effect : at the surface of the Earth we are offset from the line through the centers of Earth and Moon, and because of this we can observe a bit (about 1°) more around the side of the Moon when it is on our local horizon.
Moons
Most significant moons in the Solar System are tidally locked with their primaries, since they orbit very closely and tidal force increases rapidly (as a cubic) with decreasing distance.
Notable exceptions are the irregular outer satellites of the gas giant planets, which orbit much further away than the large well-known moons.
Pluto and Charon are an extreme example of a tidal lock. Charon is a relatively large moon in comparison to its primary and also has a very close orbit. This has made Pluto also tidally locked to Charon.
In effect, these two celestial bodies revolve around each other (their mass center lies outside of Pluto) as if joined with a rod connecting two opposite points on their surfaces.
The tidal locking situation for asteroid moons is largely unknown, but closely-orbiting binaries are expected to be tidally locked, as well as, obviously, contact binaries.
Planets
Until radar observations in 1965 proved otherwise, it was thought that Mercury was tidally locked with the Sun.
Instead, it turned out that Mercury has a 3:2 spin-orbit resonance, rotating three times for every two revolutions around the Sun
; the eccentricity of Mercury's orbit makes this resonance stable.
The original reason astronomers thought it was tidally locked was because whenever Mercury was best placed for observation, it was always at the same point in its 3:2 resonance, so showing the same face, which would be also the case if it were totally locked.
A curious aspect of Venus' orbit and rotation periods is that the 583.92-day interval between successive close approaches to the Earth is almost exactly equal to 5 Venusian solar days (precisely, 5.001444 of these), making approximately the same face visible from Earth at each close approach.
Whether this relationship arose by chance or is the result of some kind of tidal locking with the Earth is unknown.
Stars
Close binary stars throughout the universe are expected to be tidally locked with each other, and extrasolar planets that have been found to orbit their primaries extremely closely are also thought to be tidally locked to them.
An unusual example, confirmed by MOST, is Tau Boötis, a star tidally locked by a planet. The tidal locking is almost certainly mutual.


As can be seen, even knowing the size and density of the satellite leaves many parameters that must be estimated (especially w, Q, and , μ ), so that any calculated locking times obtained are expected to be inaccurate, to even factors of ten.
Further, during the tidal locking phase the orbital radius a may have been significantly different from that observed nowadays due to subsequent tidal acceleration, and the locking time is extremely sensitive to this value.
Since the uncertainty is so high, the above formulas can be simplified to give a somewhat less cumbersome one.
By assuming that the satellite is spherical, k_2 << 1 , Q = 100, and it is sensible to guess one revolution every 12 hours in the initial non-locked state (most asteroids have rotational periods between about 2 hours and about 2 days)
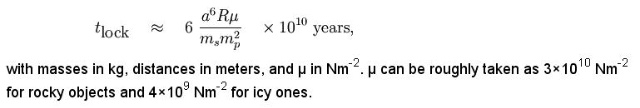
Note the extremely strong dependence on orbital radius a.
For the locking of a primary body to its moon as in the case of Pluto, satellite and primary body parameters can be interchanged.
One conclusion is that other things being equal (such as Q and μ), a large moon will lock faster than a smaller moon at the same orbital radius from the planet because m_s , grows much faster with satellite radius than R.
A possible example of this is in the Saturn system, where Hyperion is not tidally locked, while the larger Iapetus, which orbits at a greater distance, is.
This is not clear cut because Hyperion also experiences strong driving from the nearby Titan, which forces its rotation to be chaotic.
List of known tidally locked bodies
<< Solar System >>
Locked to the Sun
* Mercury (in a 3:2 rotation:orbit resonance)
Locked to the Earth
* Moon
Locked to Mars
* Phobos
* Deimos
Locked to Jupiter
* Metis
* Adrastea
* Amalthea
* Thebe
* Io
* Europa
* Ganymede
* Callisto
Locked to Saturn
* Pan
* Atlas
* Prometheus
* Pandora
* Epimetheus
* Janus
* Mimas
* Enceladus
* Telesto
* Tethys
* Calypso
* Dione
* Rhea
* Titan
* Iapetus
Locked to Uranus
* Miranda
* Ariel
* Umbriel
* Titania
Locked to Neptune
* Proteus
* Triton
Locked to Pluto
* Charon (Pluto being itself locked to Charon)
<< Extra-solar >>
* Tau Boötis is known to be locked to the close-orbiting giant planet Tau Boötis Ab[citation needed]
Bodies likely to be locked
<< Solar System >>
Based on comparison between the likely time needed to lock a body to its primary, and the time it has been in its present orbit (comparable with the age of the Solar System for most planetary moons), a number of moons are thought to be locked.
However their rotations are not known or not known enough.
These are:
Probably locked to Saturn
* Daphnis
* S/2004 S 6
* S/2004 S 4
* S/2004 S 3
* Methone
* Pallene
* Helene
* Polydeuces
Probably locked to Uranus
* Cordelia
* Ophelia
* Bianca
* Cressida
* Desdemona
* Juliet
* Portia
* Rosalind
* Cupid
* Belinda
* Perdita
* Puck
* Mab
* Oberon
Probably locked to Neptune
* Naiad
* Thalassa
* Despina
* Galatea
* Larissa
Probably locked to other dwarf planets and minor planets
Numerous asteroid and TNO moons are expected to be locked to their primaries. However, in the absence of direct observation reliable candidates are difficult to verify. While locking timescales can be estimated, the age of the primary+satellite system is difficult to gauge; most are thought to be the results of collisions in the last few hundred million years.
<< Extra-solar >>
* Gliese 581 c may be tidally locked to its parent star Gliese 581.
